如何辨识阻尼系数？

当对开关磁阻电机的定子施加正弦激励时，会引起电机定子的同频振动，振动的幅值与激励的频率有关；当激励停止后，由于阻尼系数的存在，振动的幅值呈衰减趋势，衰减的速率与定子的阻尼系数有关。实验方法辨识定子振动阻尼系数的基本原理就是通过实验测定激励停止后振动幅值的衰减速率，根据衰减速率与阻尼系数的定量关系确定阻尼系数。具体辨识原理参考文献［11］，以下仅简述主要结论。

激励停止后定子的振动由角频率为的简谐运动和指数衰减运动相结合。ζωn表示振动的衰减速度。任意t1和t2时间的振动幅值比值为

将t1、t2时刻振动幅值的比值定义为δ，则δ可表示为

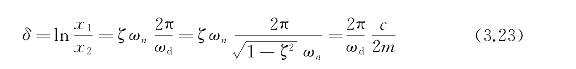
当ζ≪1时，δ≈2πζ。根据式（3.23），当得到t1、t2时刻振动幅值的比值δ时，可以间接求得阻尼比

当ζ≪1时，还可以简化为(www.xing528.com)

当正弦激励停止后，定子进入自由振动状态，由于阻尼的存在，振动幅值呈衰减趋势。在620 Hz正弦下，停止激励后，定子的振动曲线如图3.10所示。

根据式（3.24），在得到振动的衰减幅度后可以求出2阶系统的阻尼系数。首先定位出激励停止后各个周期的波峰，得到振动的包络，为了减小误差，本节使用多个周期的振动幅值进行拟合。N＝1表示激励停止的周期，N＝k（k＝1，2，…）表示振动停止后的各周期。N＝1到N＝10的振动幅值如图3.11所示。

根据式（3.23），各周期内幅值为等比数列，比值为eδ。利用最小二乘法对1～10个周期内的幅值进行拟合，得到eδ＝0.868 3。阻尼比为

图3.10　正弦激励停止后振动的衰减曲线

图3.11　衰减过程中各周期的振动幅值（N＝1～10）