【例1-5-8】 已知Quanser QUBE-Servo 直流电机等效电路如图1.5.1 所示。其中，电枢电路电感L=1.16 mH；电枢电路电阻Rm=8.4 Ω；E 为电动机电枢端反电动势（E=Kmω），ω 为电动机的角速度，Km为电机的反电势常数，km=0.042 V/（rad·s -1），它与电流方向相反。I 为电动机电枢电流；电动机轴上的转动惯量Jm=4×10 -6，直流电机轴与负载轮轴相连，轴半径rh=0.011 1 m，轴质量mh=0.010 6 kg，动惯量为Jh，轮轴带动一个金属盘（也可连接旋转摆），金属盘质量md=0.053 kg，半径为rd=0.024 8 m，转动惯量为Jd，总转动惯量J=Jm+Jh+Jd。电磁力矩常数Kt=0.042 N·m/A，建立该电机系统的传递函数。
图1.5.1 直流电机等效电路
步骤：
（1）列写出直流电机电压平衡方程。
电路方程：
电动式平衡方程：
转矩平衡方程：
其中：
。
解式（1-5-5）、式（1-5-6）、式（1-5-7）三个方程联立：
因为电枢绕阻的电感L 很小，可忽略第一项，则式（1-5-8）简化为
令初始条件为零，两边进行拉普拉斯变换，得到传递函数G（s）：
（2）整理式（1-5-10）得到简化传递函数为一阶惯性环节：
其中，
（3）代入给定参数值，建立的传递函数为：
结果为：
即：
2.建立倒立摆传递函数
【例1-5-9】 Quanser 旋转摆模型如图1.5.2 所示。已知电机反电势常数当km=0.042 V/（rad/s），电枢电路电阻Rm=8.4 Ω，旋转臂转轴连接至系统并被驱动。摆杆臂长Lr=0.085 m，其逆时针旋转时，转角θ 正增加。摆杆连接至旋转臂的末端，总长为Lp=0.129 m，摆杆质量为Mp=0.024 kg，旋转臂质量为Mp=0.095 kg，重心位于摆杆中心位置，且绕其质心的转动惯量为Jp由，旋转臂粘滞系数Dr=0.001 5 N·m·s/rad，摆的阻尼系数Dp=0.000 5 N·m·s/rad，旋转臂转动惯量为Jr，重力加速度g=9.8 m/s2。要求根据给定参数，建立状态空间模型。
步骤：（1）α 为倒立摆转角，当倒立摆在垂直位置时，α=0，计算公式为
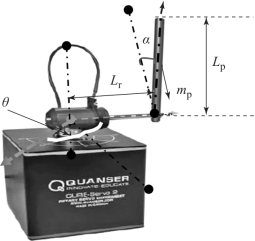
图1.5.2 Quanser 倒立摆模型示意图(www.xing528.com)
mod 为取余数，αfull为编码器测得的摆角，根据非线性运动方程为
其驱动扭矩由位于旋转臂基座的伺服电机输出，动力方程为
对非线性运动方程在工作点附近进行局部线性化，最终得倒立摆线性运动方程为
和
求解加速度项得
和
其中
根据线性状态空间方程：
式中，x 为状态，u 为控制输入，A、B、C 和D 为状态空间矩阵。对于旋转摆系统，定义状态和输出分别为
（2）由定义的状态空间模型可得
=x3和
=x4。将状态x 代入运动方程中，如式（1-5-22）给出的θ=x1，α=x2，
=x3，
=x4，即可求出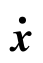
=Ax+Bu 中的A 和B两个矩阵。将状态x 代入式（1-5-18）和式（1-5-19）得
和
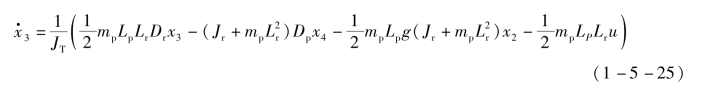
（3）旋转臂和摆杆转动惯量Jr和Jp计算公式：
（4）方程
=Ax+Bu 中的矩阵A 和B 分别为
（5）由（1-5-27）代入给定的参数，MATLAB 编程实现求取状态空间模型：
即状态空间模型为
在输出方程中，由于倒立摆系统中只有伺服位置和关节角度传感器可被检测，因此，输出方程中C 和D 两个矩阵分别为
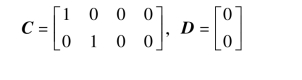
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
