静止液体的性质：真空度、连续性原理和伯努利方程

（1）液体的静压力 液体在静止状态下单位面积上所受到的作用力，即

p=F/A （1-6）

式中 p——液体的静压力（N/m²）；

F——作用力（N）；

A——有效作用面积（m²）。

在地球表面，一切物体都受到大气压力的作用并自行平衡，因此上式表示的压力，是指大于大气压力的表压力。若液体的压力低于大气压力，则称为真空度。

表压力、绝对压力和真空度三者之间的关系是：表压力=绝对压力-大气压力；真空度=大气压力-绝对压力。

（2）静压力的传递 加在密闭液体上的压力，能够以相等的值被液体向各个方向传递。这个原理称为帕斯卡定律。

如图1-42所示，在两个互相连通的液压缸中装有油液，液压缸内装有活塞，小活塞和大活塞的面积分别为A₂和A₁。根据静压力传递原理得下列公式

p=F₂/A₂=F₁/A₁ （1-7）

7.流动液体的性质

（1）流速和流量 流速和流量是描述液流的两个基本参数。流速是指液流质点在单位时间内流过的距离，其单位为m/s。流量是指单位时间内流过某一截面的液体体积，其单位为m³/s。液体在液压缸中的流速与活塞的运动速度相同，从而可建立液压缸有效作用面积、流量和活塞运动速度的一般关系式，即

Q=vA（ 1-8）

式中 Q——进入液压缸的流量（m³/s）；

A——液压缸有效作用面积（m²）；

v——活塞（缸）的运动速度（m/s）。

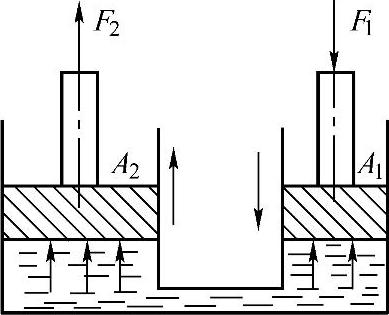
图1-42 水压机的原理

该式表明，当液压缸有效作用面积一定时，要改变活塞（缸）的运动速度则需改变进入液压缸的流量。

（2）液流连续性原理 液体在管道中稳定流动时，由于它不可压缩，在压力作用下液体中间也不可能有间隙，所以液体流经管道每一截面的流量应相等，这就是液流连续性原理。

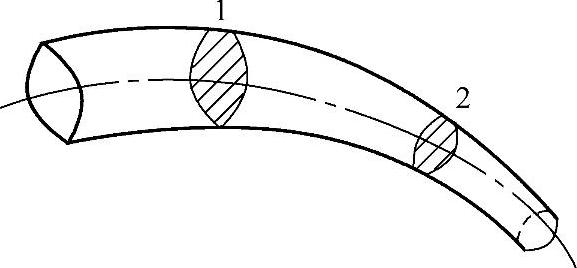
图1-43 液流连续性简图

如图1-43所示，液体在不等横截面的管道中流动，设截面1和2的直径分别为d₁和d₂，面积分别为A₁和A₂，流速分别为v₁和v₂，根据液流连续性原理，流经截面1和2的液体质量全部相等，则

A₁v₁=A₂v₂=Av=常量 （1-9）

因为Q=vA，所以液流连续性方程也可写成(www.xing528.com)

Q₁=Q₂ （1-10）

式（1-10）说明，通过管内不同截面处的流速与其横截面积的大小成反比，即管径细的地方流速大，管径粗的地方流速小。

（3）伯努利方程液压传动是借助有压流体来传递能量的。液体能量的表现形式有三种，即压力能、势能和动能。它们之间可以互相转化，而且液体在管道内任何一处的三种能量之和为常数。这就是伯努利方程，其方程式为

p₁/ρ+g₁h+v²₁/2=p₂/ρ+g₂h+v²₂/2 （1-11）

式中 p——压力（Pa）；

v——流速（m³/s）；

h——势能（J）；

ρ——液体密度（kg/m³）。

（4）液体流动中的压力损失 粘性液体流经管道及阀门时，具有一定的阻力。液体流动时要消耗一部分能量来克服这些阻力，这种能量的消耗主要体现在液体的压力损失上。液压系统中的压力损失可分为两种：沿程压力损失和局部压力损失。

1）在直径相同的直管中流动时的压力损失，称为沿程压力损失。它主要由液体流动时的内外摩擦引起。

2）由于管道截面尺寸、形状突然变化和液流方向突然改变而引起的压力损失，称为局部压力损失。

液压传动中的压力损失，绝大部分转变为热能，造成油温升高、泄漏增多、传动效率降低，所以在设计、制造和使用液压设备时，应尽量采用内壁光滑的管道，尽可能缩短管路长度，减少截面积突变及管道弯曲等。

（5）功、功率 在液压传动中，活塞在时间t内推动负载F移动距离s，所做的功W为

W=Fs （1-12）

功率P是指单位时间内所做的功，即

P=W/t=Fs/t=Fv （1-13）

经单位换算后得到

P=pQ （1-14）

式中 p——压力（Pa）；

Q——流量（m³/s）。

由于液压系统在实际工作过程中存在容积损失（用容积效率_ηv表示）和机械损失（用机械效率η_m表示），所以，液压泵实际需要输入的功率P_入

P_入=pQ/η （1-15）

式中 η——总效率，η=η_vη_m。