智能摄像机网络自校准技术

对于广阔领域的监督和监测需要摄像机网络。这些摄像机可能来自异构数据源,如云台变焦（PTZ）摄像机,静态监控摄像机以及雷达。此外,传感器根据输出特性的不同而不同,例如,视觉、红外（IR）、高光谱。用这种多模态数据的分析实现完整的情景意识和全局场景理解需要传感器的校准,它提供了摄像机在空间的排列信息和这些异构传感器的输出之间的相互作用。摄像机网络的校准（也可以参阅第9章）很重要,因为它使关键的操作任务成为可能,如地理注册、数据融合以及目标在传感器之间的切换。它还能提供一些度量信息,如检测对象在高级推理时的位置、大小、速度和前进方向。因此,最好有个自动有效机制,它能估算给定摄像机网络的拓扑结构,随着时间的推移检测拓扑结构的变化,并相应适应这些变化。

对多摄像机的跟踪^{[261,245,285]}有大量工作要做,用来解决利用学到的交通模型去估计摄像机网络的拓扑结构的问题。基于它们是否需要训练数据或用户监督,可以分为有师的^{[261,285,287,439]}或无师的^{[508,310,507,352]}方法。这里,我们使用无师的方法来说明智能摄像机如何利用从观察值学习到的场景模式来自动确定和维护它们的网络拓扑结构^[483]。

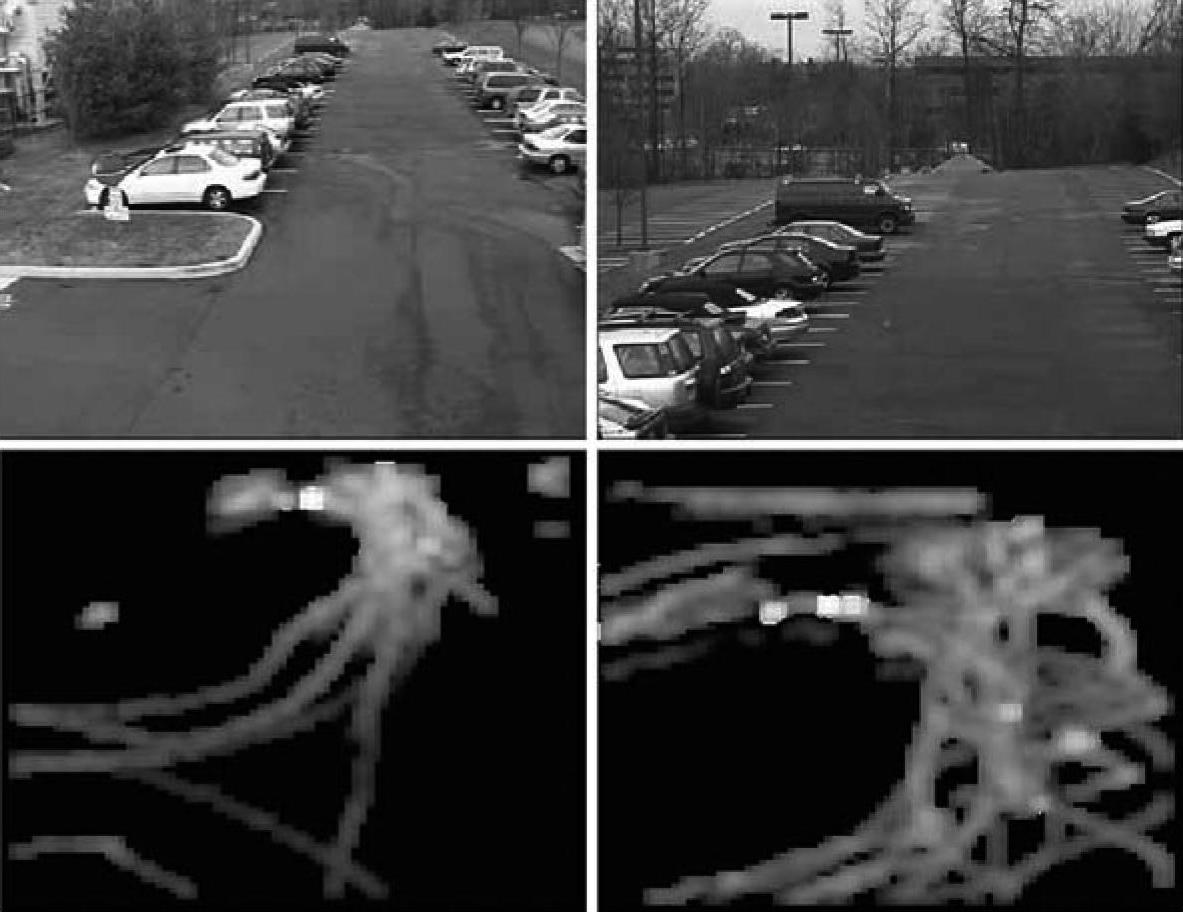
图17.9 上面一行：来自两个摄像机的图像,它们的视场存在交叠;下面一行：四维共现概率密度函数关于x、y坐标方向的二维边缘概率密度(www.xing528.com)

假设目标在场景中移动的区域是平面的（对于大多数监测方案,这个假设是合理的）,目标在两个不同传感器的观测值p和q之间的关系可以用一个单应性矩阵表示（给出一个3×3矩阵H）,即,p=Hq。给定一对传感器,它们从一个目标同时获得的观测值服从两个互补的假设,即观测值或者来自于现实中的同一目标或者是随机的数据队列。在两个传感器的相同观测位置（或附近观测位置）所获得的多次观测值满足第一个假设（注意它们也可能是频繁出现的随机数据队列）,另一方面,如果一个传感器（在特定的位置）进一步的观测值与另一个传感器（在对应的位置）的观测值不一致,就印证了第二个假设。因此,如果通过学习得到一对传感器的目标观测值的联合密度函数,那么该密度函数的模式就能表示了这对传感器视场内成对成对的观测点,而这两个传感器最可能观测到的是场景中的同一区域^[483]。通过平均移位方法可检测出以密度函数表示的这些模式,基于两个观测值的相关性测度来对这些模式进行加权（例如,Pearson相关系数）,从而解决所观测的高概率同现随机数据队列的问题。图17.9所示为两个传感器所捕获的图像及其相应的边缘概率密度（为了便于显示,取密度函数的负对数值）。可以看出,此概率密度很好地捕获到场景的公共区域。图17.10a和b所示为图17.9的最高加权模式和最低加权模式。显然最高加权模式处理后的图像与原图像具有较好的一致性,而在最低加权模式情况下不一致。一旦识别出最可能的对应图像,用基于RANSAC的方法可以估计出两个传感器之间的单应性矩阵。图17.10c所示为图17.9使用所估计的单应性矩阵获得的匹配图像。注意到该算法没有对传感器的类型和形式施加任何约束,能以类似的方式应用于有附加信源,例如,GPS/AIS数据接收器,由GPS/AIS数据提供的地理坐标可以被用于摄像机网络的地理注册。

图17.10 图a）、b）为最高加权（+）与最低加权（x）模式能用相同灰度等级的对应点来表示,图c）所估计视域的配准