共线约束下高效单应性估计方法优化

回想13.2节,给定一对传感器（C_i,C_j）,利用标准RANSAC算法从Z_ij中每次均匀采样四对点,从而得到单应性矩阵H_ij的估计。在本章的剩余部分,我们将这种算法称为RANSAC4。如果ν表示Z_ij中内点的比例,即P（I_s）=ν,则以概率ρ寻找样本中的自由外点集所需的迭代次数下限为J_RANSAC4=[ln（1-ρ）/ln（1-ν⁴）]。

考虑Z_ij中所有三阶子集（三元组）构成的集合Z³_ij。我们知道共线性在单应性变换后保持不变,即某传感器中共线点的对应点也是共线的。我们将这个特性（共线不变性）称为Q_H,将Z³_ij（Q_H）定义为满足Q_H的所有三元组的集合,即这些三元组中的点在两个传感器中都是共线的。注意对于任意三元组T∈Z³_ij,P（Q_H（T）|I_T）=1。因此,由公式（13.2）,从Z³_ij（Q_H）集合中均匀采样一个外点自由的三元组T的概率为P（I_T）=ν³/[ν³+（1-ν³）P（Q_H（T）|O_T）]。

方程中的P（Q_H（T）O_T）项表示由一个以上共线外点组成的三元组的概率。通过寻找三个共线随机点的概率来估算它。实际上,由于噪声或者传感器的有限分辨率,三个内点甚至都不可能准确地共线。因此,如果三个点形成的三角形中最短的高和最长边的比值远小于适当定义的阈值γ,则称这三点共线。我们假设OE表示三角形中的最长边,这个假设并不失一般性（如图13.1）。因此,第三点必须在OAE区域中（否则OE将不是所形成三角形中的最长边）。给定γ,模型中最短的高定义为h=γ|OE|。C是弧OA上的一点,使得d（OE,C）=h,则第三点必须位于OCTE区域中。因此由图13.1,三个随机点共线的概率估算为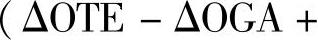,其中ΔX表示区域X的面积。另外我们知道在单应性中三元组的顺序应该保持不变,即中间的点在变换后依然在中间。因此,随机三元组共线的概率定义为。由此,P（I_T）=ν³/[ν³+0.54γ（1-ν³）]。

我们知道单应性估计仅仅需要两个非线性三元组（六对点）。因此在本章的剩余部分改进的RANSAC,称为约束随机采样一致性（CONSAC）,每次迭代从Z³_ij（3,Q_H）集中均匀采样两个三元组,下限J_CONSAC=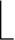ln（1-ρ）/ln（1-P（I_T）2）」。显然,对于所有的P（（I）S）=ν＞0.54γ,J_CONSAC＜J_RANSAC4。在我们的方案中,γ值选为0.04。对于γ值,只要γ﹥0.02,即数据中至少有2%的内点,本方案就会表现比较好的性能。表13.1是取不同的ν值（ρ=0.999）时J_CONSAC和J_RANSAC4的值。可以看出,基于三元组算法的理论界限按顺序优于标准算法。在第13.6节给出的定量分析结果表明本方案的实际影响更加显著。

(www.xing528.com)

图13.1 该图说明对均匀采样中随机的三点而言,如何估计它们共线的概率。A为两个半径为OE,圆心分别为O和E的圆的交点

表13.1 RANSAC算法迭代次数的下限