高效采样的特定模型属性的分析介绍

本节中,我们详细说明了存在外点的模型估计问题中,如何选择特定模型属性来实现高效采样。

设Z是一个观测值集合,M是我们想要从Z中估计出的模型。对于每一个z∈Z,I_z是一个二元指示符,当且仅当z为内点时,它的值为1,设O_z=1-I_z。基于RANSAC的方法（如参考文献[310]）从集合Z中迭代产生随机样本,然后通过样本估计一个模型M（如单应性）,再通过整个数据集合评估模型直到找到适合Z中大部分元素的模型（由噪声概率定义）或者达到了预定义的最大迭代次数。

根据贝叶斯定理,从集合Z中随机采样一个内点s的概率为

P（I_s=1）∝（I_s=1|s）P（s） （13.1）

例如,对于一个服从均匀分布的样本（如在标准RANSAC中）,P（I_s=1）=。为了简洁起见,本文中的其余部分将省略二元随机变量的值,除非另有规定,否则假设它为1。给定数据点（样本）的最小数量m,它用于估计模型M以及计算一个随机采样点为内点的概率P（I_s）,若要以概率ρ获得m个样本点中的自由外点集合,所需的迭代次数为J=|ln（1-ρ）/ln（1-P（I_s）m）|^[594]。注意J是迭代次数的一个下限,并且实际上J是相当宽松的,即估计一个好模型所需的迭代次数通常比J大得多^{[361,393,533]}。

由上面的分析容易看出,若要提高基于RANSAC的算法在带噪场景中的效率,需要找到一个采样策略,对该策略而言P（I_s）要比均匀采样中的大。此方法在参考文献[393,533,483]中得到改进,在参考文献[393,533]中,修正了式（13.1）中的先验项,从而改善了概率特性,同时式中的前一项假设了内点相互之间的距离比外点更加接近,后一项采用似然匹配法来定义采样策略。另一方面,参考文献[483]中假设通过改进的似然项P（I_s|s）,能从数据冗余中得到一个较小的子集。本文中,我们定义了一个采样策略,它利用特定模型的属性来改进这个似然项。(www.xing528.com)

设Z^l为Z中元素组成的所有l阶子集的集合。对于任意z^l∈Z^l,设且。设Q是定义在Z^l上的属性,Q（z^l）是一个二元变量,当且仅当z^l满足属性Q时,Q（z^l）为真。进一步设Z^l（Q）⊆Z^l,它是满足Q的Z^l中的所有元素z^l的集合Z^l（Q）={z^l∈Z^l|Q（z^l）=1}。

由式（13.1）和集合Z^l（Q）的定义,从集合Z^l（Q）中随机采样一个自由外点集s^l的概率为

其中

如果估计模型M时所需的Z^l中元素的最小数目为m_l,则要以概率ρ获得自由外点集的迭代次数下限为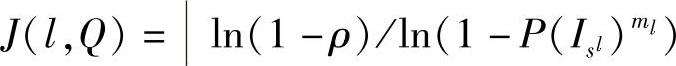。对于一个给定的模型,最佳采样策略是选遍l和Q后J（l,Q）最小的策略。实际上,可以选择满足J＞＞J（l,Q）,即的任意l和Q。该观测值和式（13.2）共同说明所选属性Q应该满足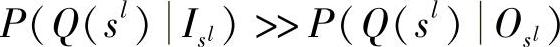。下一节,我们将列举数据驱动单应性估计问题,从而说明利用模型相关属性来实如何实现高效采样策略。