动态阈值的确定方法优化

动态阈值试图与输入数据相适应。自适应和全局阈值的一个解决方案就是将经验阈值τ和描述时变现象（它影响了变化的监测）的参数连接起来。这种现象的例子有：亮度条件的变化或者采集过程中引入的噪声。因此,测试变为

t（x,y,n）＞τ（n）（10.29）

如果阈值和全局亮度变化相适应,τ（n）是一个与观察条件有关的函数。例如,τ（n）可以是基于颜色成分的比率^[125]。如果阈值希望与采集过程中引入的噪声相适应,τ（n）可能取决于摄像机噪声的方差σ_c。

为了计算一个自适应的局部阈值,如果已知摄像机噪声的概率密度分布函数,可以用基于区域的统计分析。统计分析是以对噪声的强度分布进行建模为基础的^{[99,398,240,2,370]}。与差分图像的阈值不同的是,这种方法将差分图像中每个像素位置上小邻域的统计性能和能够影响差分图像的噪声模型进行比较。这个比较基于显著性检测。噪声模型的定义基于以下假设：邻域内所有像素的改变仅是因为噪声（假设为H₀）,序列中的每一帧都受到确定均值和方差的加性高斯噪声的影响。在这些假设下,噪声模型为χ²分布,它的性能取决于邻域内的像素数目和影响序列每一帧的高斯噪声的方差。给定χ²分布和显著性水平α,阈值τ_α的自适应值可以通过（10.30）来计算：

α=P{δ＞τ_α|H₀} （10.30）

H₀假设在测试中像素位置没有发生变化,显著性水平α是一个固定参数,不需要手动调节。

在参考文献[1]中描述了计算自适应和局部阈值的另一种不同的方法,每一个像素的空间背景信息都考虑到了。用于测试的阈值与3×3窗口W标注群c（x,y,n）相适应。当扫描图像时,只有邻域W的关联部分中的4个邻近标注是可用的。因此,其余4个值约等于之前分类c（x,y,n-1）的标注。如果K（x,y,n）表示在时间n、邻域W内检测到的变化的像素数目,那么新的测试就变为

t（x,y,n）＞τ+θ₁[4-K（x,y,n）] （10.31）(www.xing528.com)

其中,0≤K（x,y,n）≤8;θ₁是正系数,它确定t（x,y,n）的范围。这种空间自适应阈值允许产生一个紧凑的光滑形状的变化区域,降低由噪声引起的分散误差。

在参考文献[535]中呈现了这种方法的延伸。除了背景的空间信息,时间信息也被整合到自适应阈值的估计中。在这种情况下,也同样考虑前一帧中像素（x,y）的标注c（x,y,n-1）。时空自适应阈值由公式（10.32）给定：

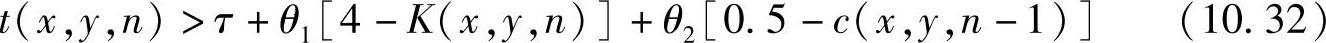
其中,c（x,y,n-1）∈{0,1},θ₁和θ₂是正系数。

用于确定变化检测中阈值的各种方法都归类在表10.4中

表10.4 用于选择分类阈值的不同方法