提取活动指数的方法与技巧

一旦输入图像转换为合适的特征并且产生了参考帧,下一步是让对应的特征与g（x,y,n）和g（x,y,r）相匹配,来估计运动等级。我们提出了一个比较特征的一般变换函数T,T是距离算子T_d和函数T₁的合成：

T=T₁oT_d （10.19）

所以,公式（10.4）可以表示为

t（x,y,n）=t₁（t_d（g（x,y,n）,g（x,y,r））） （10.20）

距离算子提供了一个像素级特征距离,这个距离可以是像素之间的差分、图像比、向量差分或一个基于二阶统计的差值度量。像素差分（图像微分）可以表示为

t_d（x,y,n）=g（x,y,n）-g（x,y,r） （10.21）

这个算子应用于代表亮度^[99,356]或颜色^[98]的灰度图像以及表示边缘^[351]和水平线^[28]的二进制图像。向量差分是一个距离度量,可以用等式（10.21）表示,但向量差是对向量进行操作：

t_d（x,y,n）=g（x,y,n）-g（x,y,r） （10.22）

这个向量可能包括颜色特征或区域特征^[153]。图像比例代表相同像素在不同时刻的灰度值之比：

这种计算可以在像素或区域级上实现且对光照变化具有鲁棒性。也可以使用基于二阶统计的差值度量。这些技术通过一些特征函数比较各像素在g（x,y,n）和g（x,y,r）周围区域的强度。在区域W中,基于二阶统计的一种差值度量是似然比^[257]：

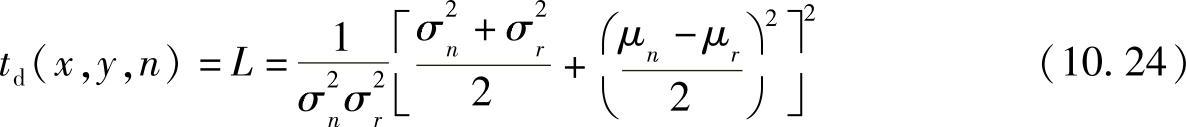
（σ²_n,μ_n）和（σ²_r,μ_r）分别是当前图像和参考图像在W中的方差和均值。(www.xing528.com)

经过距离算子T_d后,图像t_d（x,y,n）可以进一步转换得到用于变化检测的运动指数。在某些情况下,距离算子的结果t_d（x,y,n）直接作为运动指数,并且因此函数T₁作为恒等函数。这个变换T₁可以是绝对值、均方值、二阶或四阶矩以及边缘,它能应用于不同的空间支持。如果特征是图像强度或二进制掩码,比如边缘或水平线,那么在计算了距离算子后,再使用绝对值或均方值。

t（x,y,n）=‖t_d（x,y,n）‖_p （10.25）

其中p={1,2},分别代表绝对值和均方值。当特征是灰度图像（亮度或颜色组成）时在矩形窗口W计算矩。在这种情况下,假设指数为如下形式：

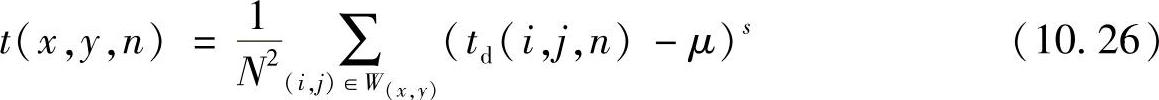
这里,t_d（x,y,n）是图像差分或者是图像比例;s是矩的阶次;μ表示均值,如下：

t_d（x,y,n）和s的不同组合已经应用于计算活动指数。在参考文献[398]中,t_d（x,y,n）是光照强度的差和s=4时的结果,t（x,y,n）是一个四阶矩。在参考文献[502,153]中,t_d（x,y,n）是亮度值和s=2的图像比。因此,t（x,y,n）是二阶矩（明暗模型）。这个活动指数可以由整个区域^[502]（重叠窗口）或中心像素^[153]（不重叠窗口）得到。第二种解决方法提供了一种更好的空间分辨率。

计算距离度量,T₁是一个边缘检测器,它提供光照变化的鲁棒性。在参考文献[98]中边缘检测采用索贝尔算子,并且图像微分适用于三种颜色分量。

表10.3 特征分析技术用于计算活动指数

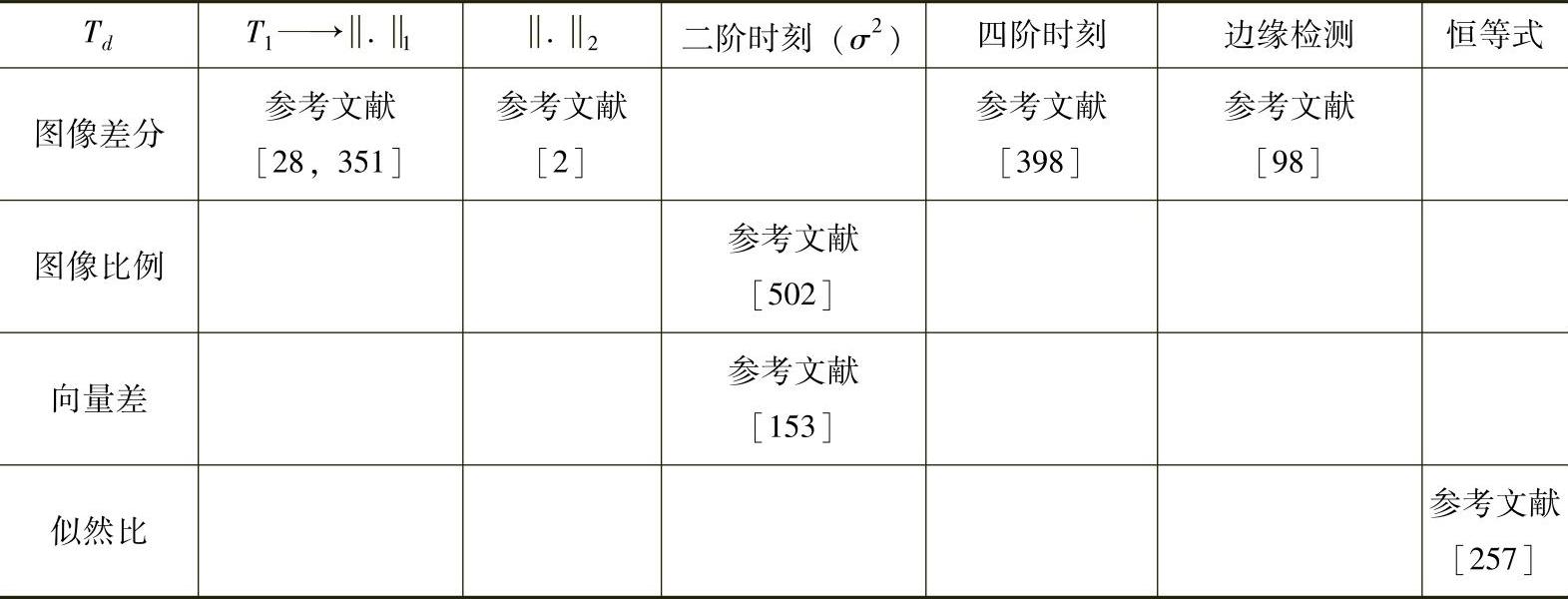
表10.3总结了本节中所分析的不同变换。