灭点约束与双线性关系的重构：世界坐标系中的正交灭点用于计算ω

已知两个世界坐标中方向的围角,它们的灭点在视觉信息和场景信息分析中具有较高的利用价值。让我们不受任何限制地假设世界坐标系在摄像机中心,等同于摄像机坐标系,或更正式,P=K[I₃0]。摄像机中心发出的每条光线都有其特定的方向,因而在世界坐标系中也具有特定的方向。这些射线在灭点穿透像平面。直觉上,封闭角告诉我们,像平面到摄像机中心的最短距离是焦距,是K的一部分。可以这样想象,更多的射线对和角度将能计算出所有的内部参数。

在数学上,我们把两个方向d₁和d₂的交角用ϕ表示：

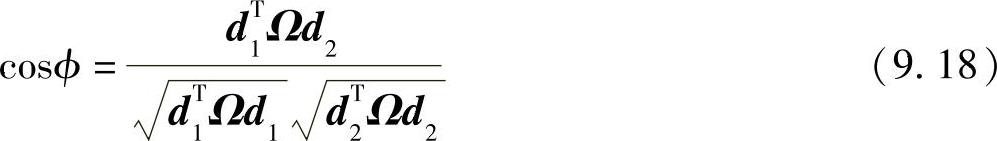
这是欧几里德空间的所有方向内积,即Ω=I₃。通过利用K把这些方向映射到它们的消失点,然后用ω取代K^TK^-1得到下面公式：

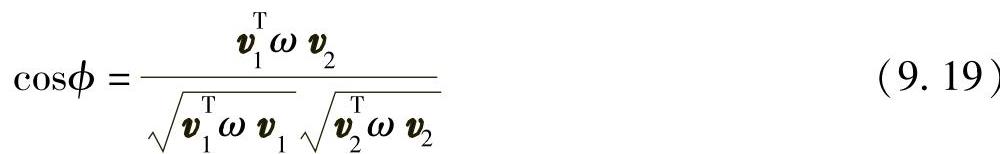
这是未知量ω,两个灭点（视觉信息）以及ϕ（场景信息）之间的一个非线性关系。

在特殊情况ϕ=π/2下（如图9.4）,上述关系简化为(www.xing528.com)

v^T₁ωv₂=0 （9.20）

这是未知量ω的为双线性关系,但可以重构为线性关系（等式9.17）其中ω由w所取代^[229]。这种关系提供了一个对ω的约束,因此,5个独立的正交灭点对足以计算ω。

正交灭点也告诉我们摄像头对于世界坐标系的相对旋转;正交灭点是成像坐标轴世界坐标系的方向。改变了像素灭点的位置会改变摄像头的方向。不幸的是,如果没有更多场景信息,真实世界中的上、下、左、右这些关系是未知的,则绝对的旋转是不能识别的^[2]。

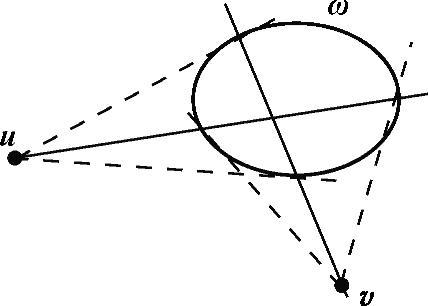
图9.4 正交方向的灭点相对于ω共轭正交,因此限制了ω。例如,（第9.4节）世界坐标系上正交平面平行线与灭点u和v成几何影像,v在u关于ω的极线上,u在v的极线上,极线分别由通过u和v的ω的切线来定义（称为极点）^[479]