内部校准的关键——ω矩阵的计算与条件优化

内部校准是基于参考文献[174]的一个重要结论——用投影几何的语言来说,K的估计值与用一个3×3矩阵ω描述的图像Ω内在相关,ω矩阵如下：

这个矩阵被称为IAC。

上一节作为P的一部分引入了H∞,它将无穷远几何实体映射到像平面,因此,我们由下式将ω写作Ω的曲线映射。

ω=H^-T_∞ΩH^-1_∞=（KR）^-TI₃（KR）^-1=K^-TRR^-1K^-1=（KK^-T）^-1 （9.16）

IAC中的ω和K是双射关系;已知K可以直接计算出ω,而已知ω也可以通过矩阵求逆和Cholesky分解^[1]来得到K。与Ω一样,ω是虚点二次曲线,与K不同,可以直接按照约束条件通过视觉、现场和摄像机信息进行计算。

表9.1给出了计算ω的五个充要条件。ω是一个对称的齐次3×3矩阵,秩为2,因此有6-1=5个未知元素是独立的;ω独立元素的个数等于K的未知元素的个数。所有的约束条件都是线性的,这样就可以用矩阵A表示（参见参考文献[229]的第225页中的算法8.2）未知数ω的一个齐次线性方程组。

Aw=0 （9.17）(www.xing528.com)

其中w=（ω₁…ω₆）T表示未知数。5个独立的方程加上一个假设‖w‖₂=1得到一个特解。例如,通过使用SVD,把A分解成A=UDV^T的形式。D的对角线元素全为正,非对角元素全为零。如果D的对角线元素是一个降序排列,那么ω是V的最后一列。灵活地使用不同约束条件（信息来源）的特点,使得大家喜欢用这种方法进行内标定。另一种方法是构造K中元素的二次三角约束方程,但是这种方法显然不够灵活。

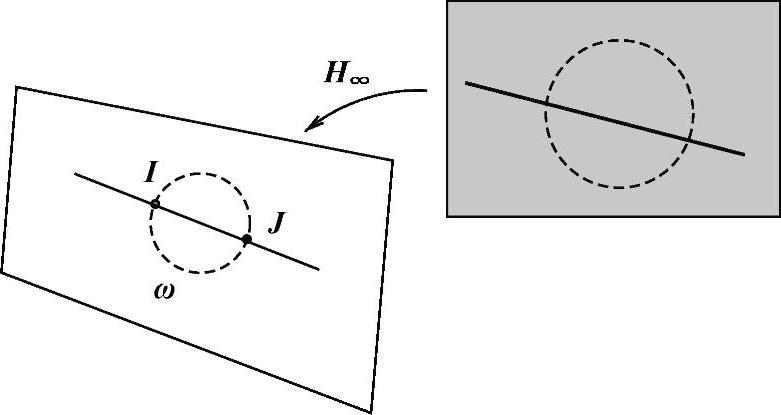
图9.3 H_∞将Π_∞上的几何实体映射到像平面。例如,Ω被映射到ω,平面上的虚圆点被映射到ω上的I点和J点,因此受到ω的限制。

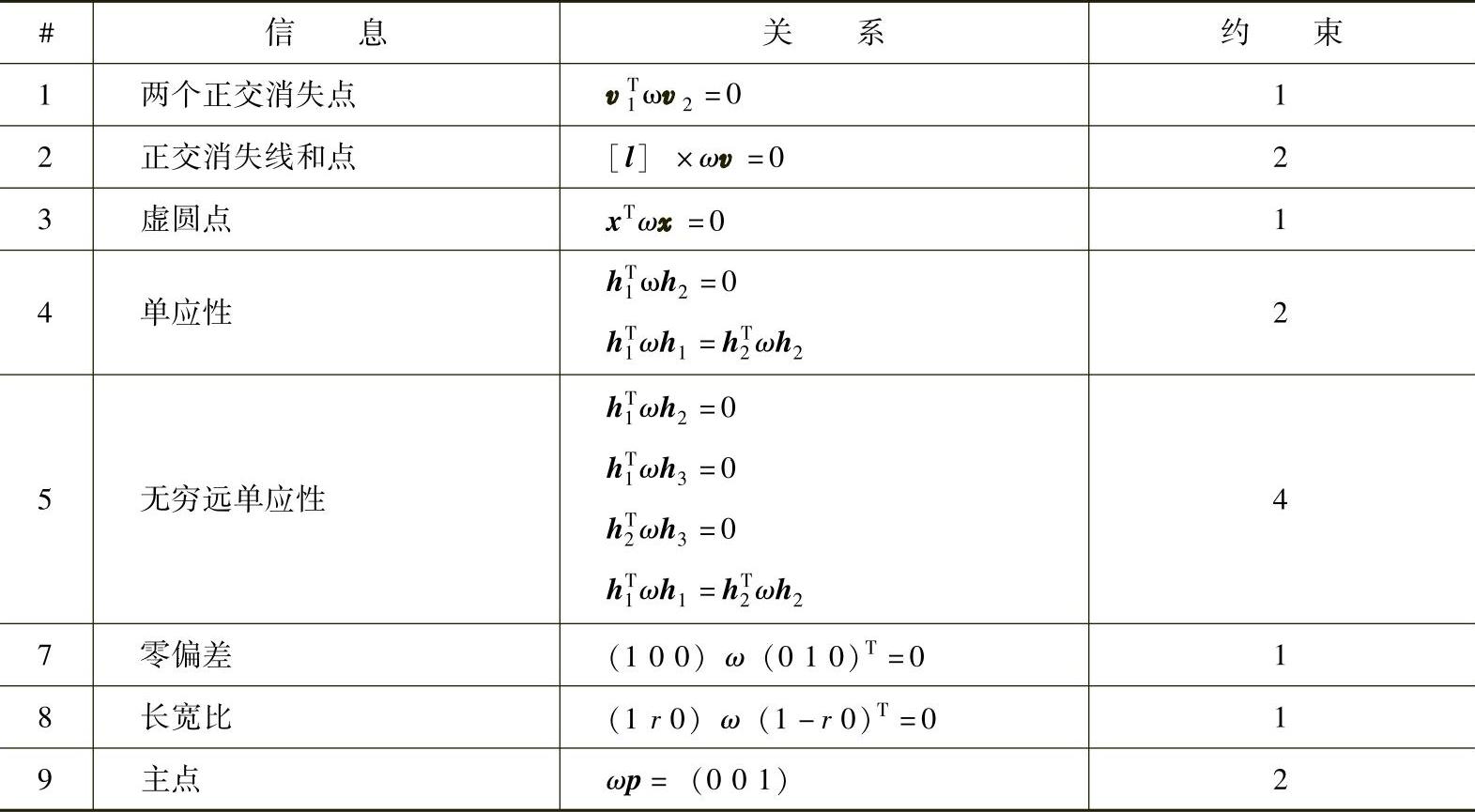
表9.1 具有视觉、现场和摄像机信息的ω的计算。其中[·]×是斜对称矩阵运算符（式9.22）

有时候方程会超过未知数,这会产生没有解的过约束方程系统。然而,使得‖Aw‖₂最小的最佳近似解可以由SVD计算出来,SVD成为了求解准确约束和过约束方程组的便捷工具。

我们仔细观察各种能够使我们计算出ω的信息来源,有些关系是相互联系的,我们将讨论这些交叉关联。