齐次坐标下的无穷远表示方法

齐次坐标的另一个重要优点是点、线和二次曲线在无穷远处的表示方法。例如一个无限远的平面点有一个零齐次坐标,并且可以描述平面上的方向。可以选择一对点x₁和x₂来计算平面在无穷远处的线。

L_∞=（x₁₁x₁₂0）^T×（x₂₁x₂₂0）^T=λ（0 0 1）^T （9.6）

该方程表明不论我们选择哪一对点,对于特定的平面L∞都是一样的,因为所有可能的平面方向最后都是一条线。请注意,要区分不同平面是不可能的,除非参照系是欧几里德三维空间：因此L_∞是一个常向量。同样,无穷远点,三维点是一个四维向量,代表空间中所有可能的方向,例如,如果宇宙是我们所处的空间,那么在天空中所有的星星构成无限空间的特定方向。天空是一个几何球体,被称为无穷远处的平面П_∞（如图9.1）。所有无穷点的平面点构成了所有可能的无穷远的空间点,因此组成П_∞。

П_∞内嵌两个重要的几何实体：虚圆点和绝对二次曲线,它们包含了内部标定的场景信息。L∞和所有欧几里德平面都有两个复共轭虚圆点,X_I=（l i 0）^T以及X_J=（l-i 0）^T。虚圆点是平面上每一个可能的圆和L∞的交叉点。圆是当c₁=c₃和c₂=0时特殊的二次曲线。虚圆点反映了欧几里德平面上诸如角度和长度比率的度量特性。(www.xing528.com)

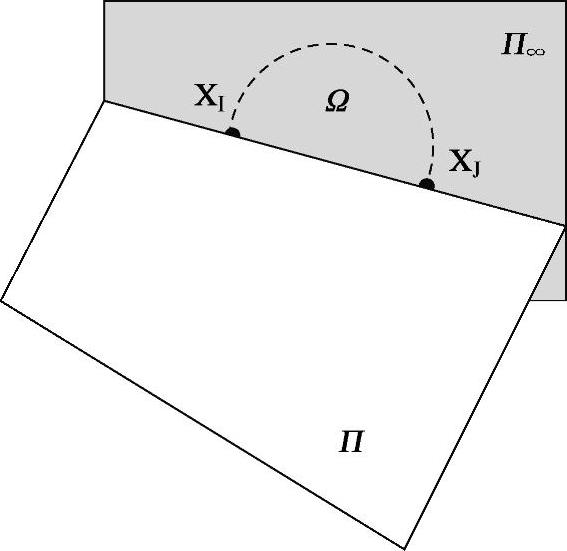
图9.1 欧几里德三维空间中每一个平面П与无限远平面П_∞相交于一条线,这条线由П所约束的所有可能方向的点组成。П_∞是一个理论上的几何结构,在无穷远处将空间封闭起来。两个圆周点X_I和X_J有特殊意义。它们构成度量属性如角度和线比率。这两点是无穷远处平面的线和构成空间所有平面的绝对二次曲线Ω（由空间所有可能平面的虚圆点组成）的交点。

当我们把参考系从平面转到空间时,一个几何实体——П_∞上出现了绝对二次曲线Ω,在这种情况下,它是由所有可能平面上的所有可能虚圆点组成的。以X_I和X_J为例,Ω实际是一个以i为半径的圆,即Ω=I₃是一个3×3的单位矩阵。空间每一个特定平面的L_∞与平面曲线Ω相交于两个虚圆点（图9.1）。参考文献[174]介绍了Ω,它在内部标定中起了重要的作用（9.3节）。