立体匹配算法介绍及应用研究

从1980年出现立体匹配算法这个概念以来,已经出现了多种立体匹配算法。在不考虑处理时间的情况下,很多算法的效果都很好。对于嵌入式系统,处理时间和高帧率是必需的,任何情况下都应该达到10fps,而且算法应该具有实时性,这就意味着计算必须在一定的时间帧内完成,还必须独立于当时的真实场景（actual scene）。现有研究表明,基于相关性的（correlation-based）算法是最适合嵌入式系统的实现的。参考文献[89]是一篇很好的关于实时立体图像匹配研究现状的综述,该文只提到了基于相关性的算法。本章将详细介绍两种基于相关性的立体匹配算法,第一种是大家熟知的绝对值差分求和法,另一种是参考文献[588]介绍的相对复杂的census变换。

一般地讲,基于相关性的立体匹配算法的步骤如下：第一步,计算所有像素的匹配代价以及所有存储在三维数据结构中的视差,这被称为视差空间图（Disparity Space Image,DSI）。匹配代价定义了正确匹配的概率,即代价越小,概率越高。为了提高正确匹配的概率,可以做这样一个假设：除了断点,相邻的像素都有相同的视差。所以第二步要计算每一个像素周围特定窗口内的总代价,这个算法的缺点是物体边界在视差图中变得更宽。DSI保留了每个视差层次下所有像素的总代价。最后一步是找出具有最低代价的视差层。局部方法是从邻域中选择一种独立于其他像素且具有最低代价的像素进行匹配。最常见的一种方法是胜者优先（winner takes all,WTA）,在所有可能的视差值中搜索最小值或最大值。全局方法是用扫描线或整体图像为每个像素指定视差值。全局方法包括动态规划^[409,63,215],图割（graph cuts）^[73,299],以及置信度传播^[515]。绝大多数全局方法计算成本很高,目前无法实时实现。只有动态规划能够用于实时匹配^[185],但是它产生的视差图有水平条纹,这是一个主要的缺点。匹配可以从右往左,反之亦然,所以遮挡点和不确定匹配能通过左右相容性检查过滤掉。这就意味着,只有在两个方向都相同的视差值（在一定的范围内）才被设定为有效。最后,计算摄像机光心的正交距离、三维点云,进行三维重建。图8.3是上述立体匹配算法的原理流程框图。

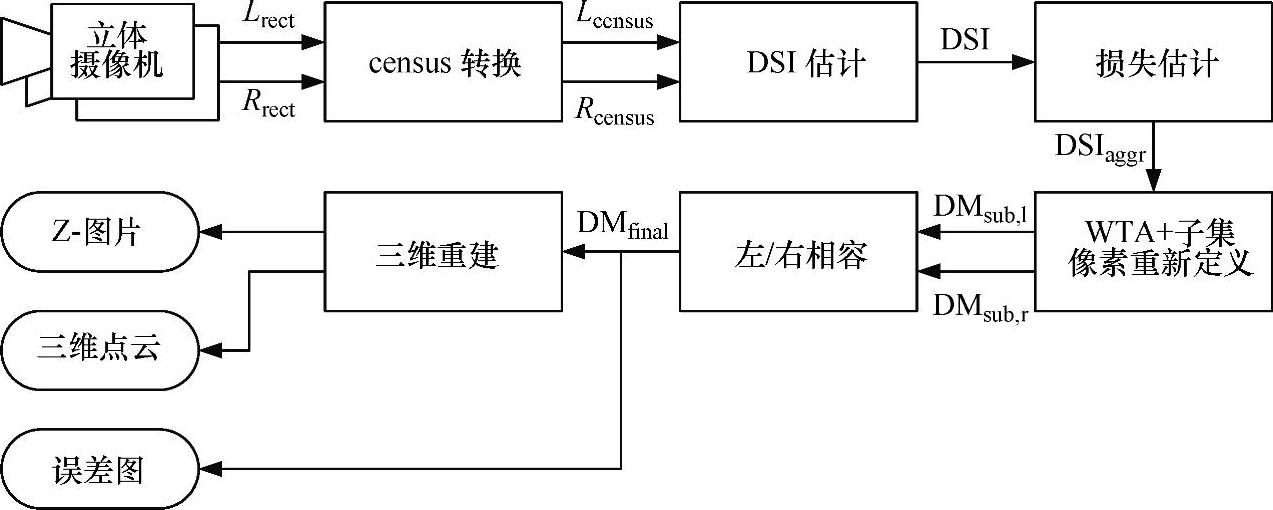
图8.3 立体匹配算法的原理流程框图

工作流程的第一步是通过立体头获取立体图像（假设无畸变且经立体视觉几何矫正）（stero image acquisition by the stero head）。本算法使用黑白图像输入,因此使用黑白摄像机就很方便,不需要再把彩色图像变为灰度图像。与贝尔模板图像相比,黑白摄像机传输的图像更为清晰,而且噪声较低。另一个重要的方面是立体图像捕捉的同步性,尤其是在摄像机头或者捕捉场景是移动的情况下,图像获取必须尽可能是同时的（很多摄像机都有外部触发输入,它提供了同时精确触发两个摄像机的可能性）。

在census匹配算法中,先对图像对进行census变换,该变换取决于实际像素和确定窗口内像素之间的局部强度关系。这个关系由下面的函数定义：

这里,p₁和p₂是图像的像素;census变换由式（8.5）为左、右图像中的每个像素产生比特流L_census和R_census,如式（8.6）和式（8.7）所示,运算符表示逐位连接运算;n×m是窗口的大小：

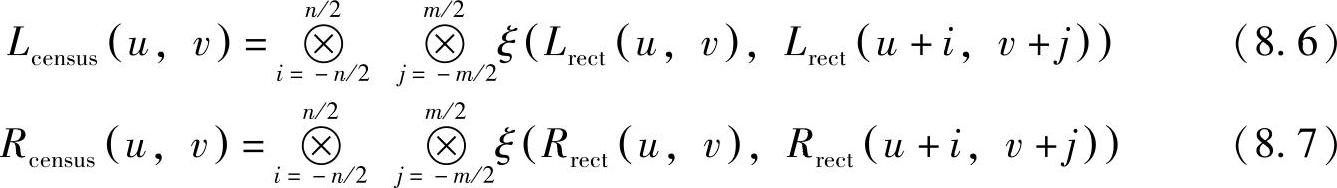
下一步是匹配部分。必须计算每个像素可能的匹配代价。匹配是在一定的视差范围d_start～d_stop进行的。计算结果存储在大小为长（disps）×宽×高的视差空间图中。如图8.4所示三维矩阵中的一个切片是一个视差层。

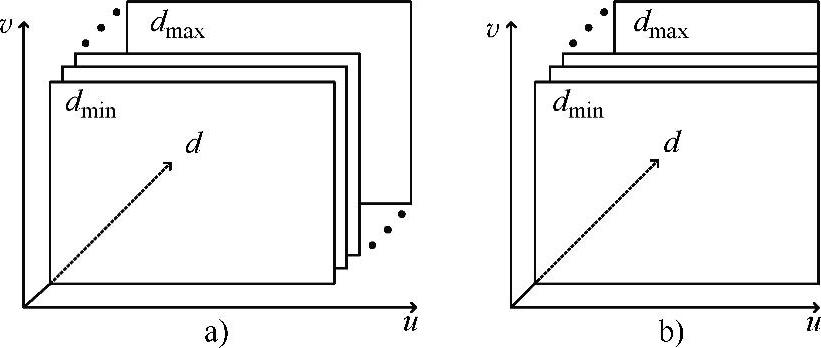
图8.4 两种DSI可能性

a）标准型 b）内存简化型（memory reduced）

左边是标准的DSI,右边是内存简化型。DSI的大小是可以被简化的,因为对每个视差层（disparity level）来说,仅有宽度为d的像素是可能的匹配集。如果匹配是从右往左进行的,则如图8.5所示,右边图像右侧的像素没有匹配点,这些像素数量随着视差层的变化而增加。

图8.5 DSI宽度随着视差水平变短

计算两种census变换像素的代价函数,等同于计算两个比特流之间的海明距离。式（8.8）计算了整个DSI中图像的census变换：

∀d∈[d_start,d_stop]：DSI_d（u,v）=Hamming（R_censust（u,v）,L_census（u+d,v）） （8.8）

对SAD,代价函数是两个像素强度之间的绝对差,它会改变DSI的计算：(www.xing528.com)

∀d∈[d_start,d_stop]：DSI_d（u,v）=R_rect（u,v）-L_rect（u+d,v） （8.9）

定义一个简单的方形窗口滤波器计算代价和：

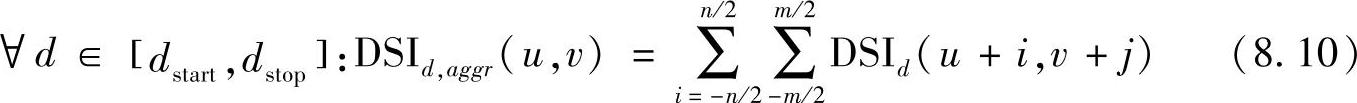
计算完所有可能的匹配之后,就应该寻找最好的匹配。迄今为止,绝对值差分求和与census变换两种方法的处理步骤是相同的。正如前面所说,代价最小为匹配最好。图8.6给出一种典型的代价函数。黑色圆圈表明整数级视差层的代价,可以看到在误差水平d_min时代价最小,这个水平就是通过胜者优先的搜索方法获得的。

图8.6反映了整数级视差,但是在大多情况下真正的视差是介于二者之间的。为了计算所谓的亚像素视差,采用抛物线拟合的方法。最好的整数级视差和它的邻点被用来扩展（span）图8.6所示的抛物线,并且它的最小值就是亚像素的视差。现在及以后,y（d）表示某一像素在视差d时的确定匹配代价。一个像素的亚像素视差计算方法如下：

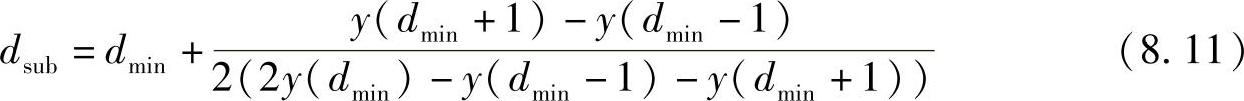
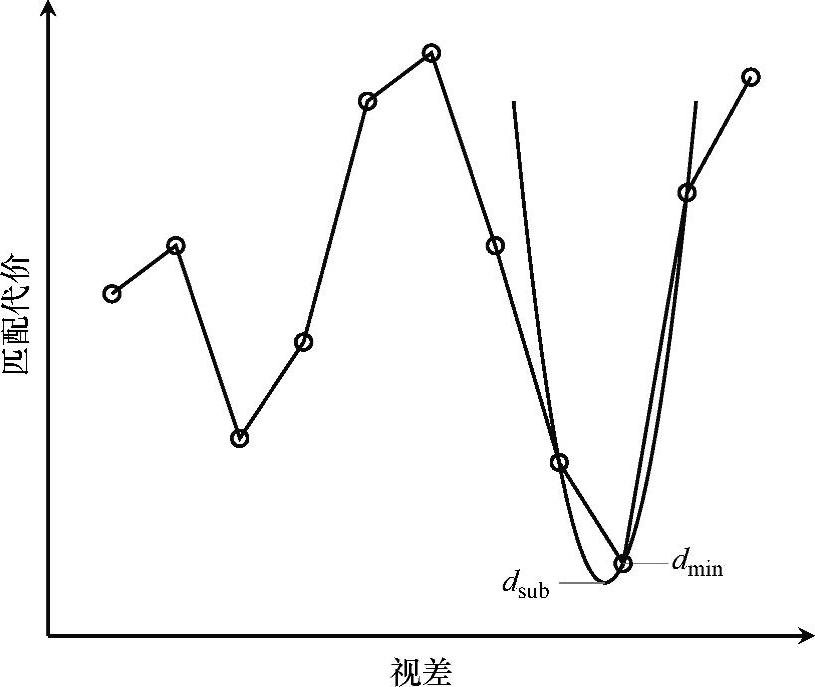
图8.6 损失函数实例

公式中的坐标（u,v）被省略。在亚像素准确度上,整个视差图在两个匹配方向上的计算由以下公式完成：

DM_sub,l（u,v）=d_sub,l（u,v） （8.12）

DM_sub,r（u,v）=d_sub,r（u,v） （8.13）

为了滤除遮挡点和不确定的匹配,对DM_sub,l与DM_sub,r做左/右相容性检查来确定最后的视差图DM_final：

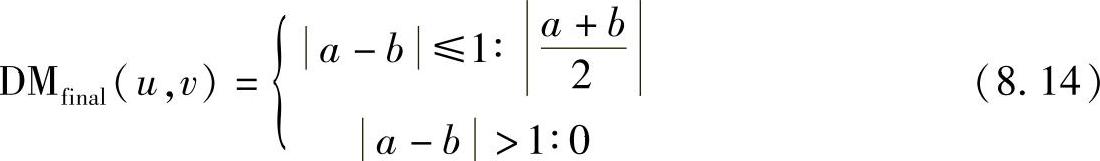
这里：

a=DM_sub,l（u,v）b=DM_sub,r（u-a,v） （8.15）

最后一步是利用式（8.3）计算Z图像,利用式（8.4）考虑左摄像机坐标系统的三维点云。图8.7显示了绝对值差分求和（SAD）与census变换得到的最终视差图数据集,三个数据集来自Middlebury Stereo评估网站^[5]。

图8.7 用于绝对值差分求和与census变换两种方法产生的视差图数据集