不同优化方法对256.1表示方法的运动分析效果评估

这一部分给出了在VC4465模型上实现和测试KLT追踪算法^[532]的实例,该模型包括一个1GHZ的TMS320C64×处理器以及一个768×582像素的图像传感器,展示了智能摄像机进行实时追踪的可行性。KLT算法的主要思想就是在一系列图像中追踪到重要的图像特征。特征就是一些小图像窗口W（一般是7×7像素）其中包含一些纹理信息。首先有选择地对它们进行平滑（去除噪声）,然后对图像进行微分,选择水平和垂直边缘均为最高幅度值的那些窗口。接着通过迭代程序对每个窗口进行一帧接一帧地追踪,该程序估计出图像的位移,然后以亚像素的精度匹配特征。这个过程重复进行,直到错误小于一个给定的阈值。图像位移的估计是以图像梯度信息为基础的,且涉及窗口W上的四个积分行列式的计算。尽管估计本身是耗时的,但是它通过减少W的匹配数,从本质上减少了计算时间。

6.3.1.1 方法论

VC4465摄像机通过局域网与外界环境进行通信,但没有足够的带宽来保证原始图像以一定的速率传输,难以使得序列图像能被储存起来并用来测试。由于摄像机仅有64MB的RAM和4MB的闪存,用于图像保存并非好的解决方案。因此,为了获得可重复再现的结果,大多数图像序列的统计计算在PC机上进行。最后,除了对6.2.1节中所述的内存管理以及输入输出函数的改进,在Intel/Windows环境以及智能摄像机上都使用了相同的代码。

6.3.1.2 优化KLT跟踪代码的浮点版本

在智能摄像机上实现该代码的第一步是修改现有的用于PC的代码,从而使得修改后的代码在摄像机的DSP上能够正确编译且没有警告。最初的FLKlt运行在DSP上时,每个像素的计算都采用了纯浮点数,对于几乎没有运动的图像序列,处理速度为1.1帧/秒（fps）,对于高速运动的图像序列,处理速度为0.6帧/秒。高速运动的图像内容使得算法要执行窗口搜索微调过程中所有的八个循环。在最初尝试加速计算的时间时,我们使用了TI TMS320C62x/64x快速运行时间支持库（Fas_- tRTS）^[1],其中包含了单双精度的浮点运算模拟函数。取代原来运行速度慢的函数后,追踪器的运行速度提供了大约2.5倍。目前为止,对于实际应用来说,该代码仍然不足够快。

6.3.1.3 移植到定点运算

在定点处理器上模拟浮点运算是无效的,两个浮点数值的乘法运算需要35个时钟周期,加法运算则达到81个时钟周期。因此我们的目标是尽可能地消除代码中所有重要部分的浮点运算。特别指出,需要采用定点运算来优化下面的这些计算功能。

①图像中水平及垂直变化的梯度运算;

②图像的水平及垂直平滑;

③亚像素精度的特征窗口插值（在计算积分中需要用到,因为需要在亚像素精度下进行W的匹配）;

④计算特征窗口的积分。

需要解决的主要问题是,如何用整数表示从0到1变化的数字？这种问题将出现在计算变化率、平滑图像、直线切削图像以及计算位移等情况。如果考虑用n bit存储一个数字,那么可以分配i bit给整数部分,剩下的（n-i）bit给小数部分。整数部分所包含可能数值的总数定义为取值范围（2ⁿ）,小数部分中两个连续值的最小差值定义为精度（1/2ⁿ）。下面是一个8bit无符号整数的简单例子：

这是数值范围为256、精确度是1的数字,因为它能表示2⁸=256种不同的值,且两个连续值之间的最小差别是1/2⁰=1。这种表示方法定义为256.1。如果分配4bit给整数部分,余下的4bit给小数部分,结果会是

这个数值的范围是2⁴=16,精度是1/2⁴=0.0625（定点16.16）。在定点数字上的算法运算操作是十分简单的。尽管如此,我们应该注意到,正常情况下两个16bit的数字相乘的结果是32bit,其中小数部分是16bit。当这些额外的位数不可用时,将会产生溢出。解决的办法就是使用有效位数的一半来存储数值。

执行完算术运算之后,结果必须经过适当的移位来获得定点数,使之达到正确的数值范围和精度。这种方法的缺点就是32bit的整数只能有效地存储16bit的数值。最终的KLT代码中的数据表示方案如下：

①16bit有符号整数值代表代码中的所有数值（特例看下面）;

②保留8bit作为数值的整数部分（一般情况下使用8bit数值表示图像像素值）;

③剩余的7bit表示数值的小数部分;(www.xing528.com)

④坐标值作为32bit的有符号数值存储（其中7bit是精度）;必要的时候转变为定点格式,这使得算法能在宽高都为256像素或更大的图像上进行操作。

在较长的计算中变量仅存为16bit的数值,中间结果尽可能地暂存为32bit。只有当必需的时候,这些值被转换为16bit。既然估算特征位移的行列式计算需要一个很大的数值动态范围,这种情况下需要80bit（由TI编译器支持）的整数。这种选择并没有引起程序执行时间上的明显减少,因为对每一个特征窗口W的匹配只需要进行一次行列式计算,而且80bit整数的计算比使用浮点运算还要快速。

在算法中实现的C代码,采用的整数运算显然已取代了原始的浮点代码,因为在大多数情况下,变量及其使用都是一致的。因可视化的需要,必需改变基础数据类型,且需调整它们的编译。

我们也试着使用单指令多数据流（SIMD）的指令来优化代码。然而,SIMD指令在该处理器上工作需要16bit或者8bit的数字。当把数值范围缩小到3bit,精度降低至4bit时,该算法就不能正常运行了,因此只能放弃这种想法。

6.3.1.4 执行次数

对于所有函数的实现,我们测试了单次追踪迭代的执行时间。对于几乎没有运动的场景,主要涉及KLT算法的梯度运算以及平滑部分,计算行列式所需要的时间明显要少于高速运动场景的时间。因此我们选择了6.3.1.2节中所描述的两种不同的场景（低速运动和高速运动场景）,来评估不同优化方法的效果。下面的配置用于KLT追踪器的所有测试项目中：

①384×291像素的图片;

②150个跟踪点;

③7×7像素的窗口;

④最多8次迭代的特征细化。

表6.3说明了单次跟踪迭代时间在经过每一步优化之后是如何降低的。

表6.3 单次跟踪迭代时间以ms计。测试平台为VC4465摄像机,内含1GHz的TI DSP

即使是在PC机上编译,定点版本每帧仅需要22ms,而原始的浮点代码则需要24ms,前者略快一点。这就意味着即使在PC机上使用定点代码也能获得适当的增速（不需要使用现在所有的现代处理器上都可用的SIMD指令）。

6.3.1.5 比较定点和浮点的跟踪准确性

为了测试方案的准确性,采用了一群人在地下车站向电梯移动的序列图像,包含799帧图像,帧率为15Hz。为了进行估计,选择了150个跟踪点,追踪过程在798帧图像中逐点执行。然后,在定点和浮点实现时,所有对应点之间的绝对差值体现在一个直方图中。结果如图6.1所示。点坐标的平均精度是0.75像素。

总之,点追踪的实时算法能够合理地移植到具有定点算法处理器的智能摄像机上,并达到满意的精确度。在代码中,精心调整变量的整数或者小数部分,可以在速度和精度之间取得平衡。当分辨率为384×291像素,帧速率为30Hz时,KLT追踪器在1GHz的TI数字信号处理器上可以正常工作。

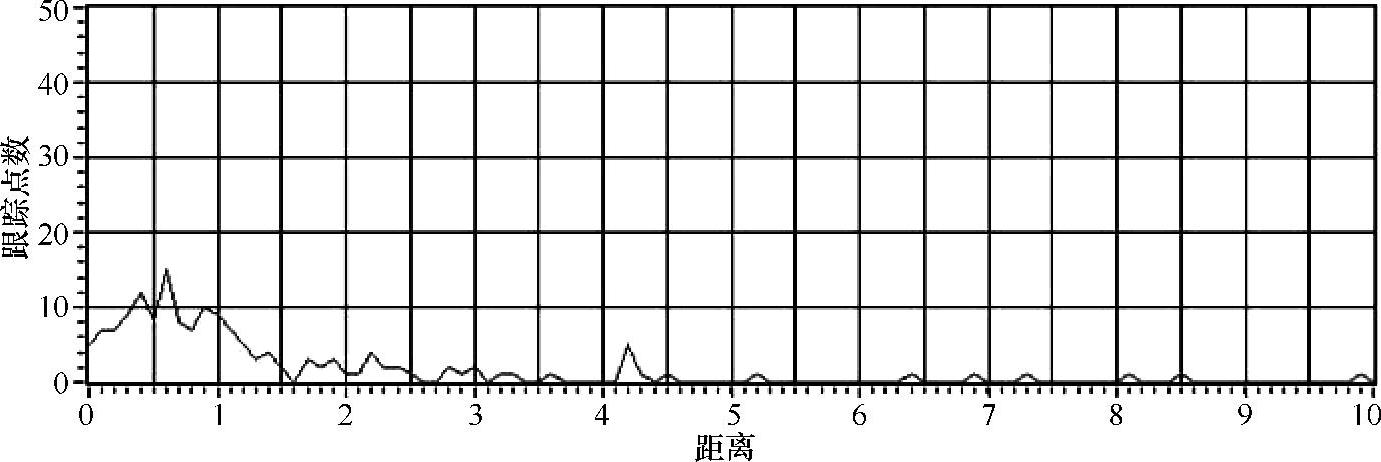
图6.1 追踪点位置间的累计差值直方图