用非加法器芯片实现加法功能的拓展进阶

1.基于门电路的加法器设计

(1)设计要求

用与非门设计一个输入范围为-3～+3的整数加法器，并通过共阴极数码管显示运算结果。

1)输入定义

电源电压为5～6V，用两个4位拨码开关输入两个加数对应的二进制补码(正数的补码就是原码;负数的补码是原码的反码再加上1)。每个拨码开关作为一个加数，并且定义每个拨码开关是从左到右、从低位到高位，开关闭合代表该二进制位是1、断开是0。逻辑电路图中定义的输入变量按从高位到低位的顺序排列为A3、A2、A1、A0;B3、B2、B1、B0。

2)输出定义

本电路最终输出为两个七段共阴极数码管上的数字，其中一个数码管显示数字;另一个数码管显示正负符号。

(2)电路设计方案

1)设计原理

根据人们平常使用计算器的常识，该加法器应包括“输入电路”“运算电路”和“译码显示电路”3个部分，其组成系统原理框图如图2-30所示。

图2-30 加法器组成系统原理框图

2)设计方案与论证

①输入电路。采用拨码开关实现4位二进制补码的输入。电源使用输出电压为5.24V的移动电源。

经实测，5.24V满足与非门芯片74HC00N最低高态输入电压的条件，拨码开关在接入上拉电阻后也能满足向74HC00N输入高低电平的需求。

②运算电路。方案一：设计一种电路，当用户输入两组4位二进制码之后，能直接输出其对应的计算结果，如图2-31所示。

图2-31 直接输出对应结果的加法运算电路

方案二：用4个全加器级联，实现4位二进制相加，如图2-21所示。

方案三：将电路分成两部分，先将进位全部算出，再将加数与进位一起运算，得到最终的计算结果，如图2-32所示。

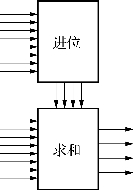
图2-32 先进位的加法器

方案讨论：方案一虽然理论上运行速度是3种方案中运行速度最快的，但是它涉及的卡诺图较为复杂，化简时容易出错;方案二是将加法器分解出易于设计的全加器，能在短时间内设计出正确的电路，但是因为级联电路必须等待上一位进位计算完成后才能计算下一位，所以运算速度较慢;方案三结合了方案一、方案二的优点。但是考虑到本设计任务只需实现4位二进制加法运算，所以3种方案在运算速度上并没有明显差异，故选择易于实现且不容易出错的方案二。

③译码显示模块电路。对于数码管显示方式，有以下两种显示方案。

方案一：数码管显示“6”时，不显示“a”段，如图2-33所示。

图2-33 数码管显示“6”时不显示“a”段

方案二：数码管显示“6”时，显示“a”段，如图2-34所示。

图2-34 数码管显示“6”时显示“a”段

方案讨论：对比方案一和方案二不难发现，它们的区别在于“6”的显示方式。虽然两种显示方式都不影响“6”的读数，但是若选用方案二，则数码管的a段与d段便能同时点亮或熄灭，这就意味着在译码器电路设计时，a段与d段可以共用一套电路，从而使与非门使用的数量减少。因此选择方案二的显示方案。

(3)硬件设计

1)开关电路的设计

考虑到74HC00N输入引脚不能悬空，因此在开关和与非门之间接一个10kΩ的上拉电阻，使得当开关断开时，与非门输入引脚接地，实现低电平输入，同时避免芯片的损坏，如图2-35所示。

图2-35 开关单元电路

因为输入数值范围为-3～+3，它们对应的4位二进制数的补码分别为1101、1110、1111、0000、0001、0010、0011，不难发现最高位和次高位同时为1或同时为0，所以最高位和次高位可以共用一个开关S3，向运算电路输入11或00。因此所设计的输入电路如图2-36所示。

2)运算电路的设计

设两个输入加数分别为A、B，进位输入数为Ci，进位输出数为Co，设计过程如下。

图2-36 开关输入电路(www.xing528.com)

①将异或运算变换成与非运算。为了用与非门设计全加器，需要将全加器的逻辑函数表达式(2-10)中的异或表达式用与非形式表示。

②画出与非门形式的异或门。根据式(2-11)，画出与非门形式的异或门如图2-37所示。

图2-37 与非门形式的异或门

③用与非门形式的异或门实现一位数全加器。将图2-37所示的异或门代替图2-18中的异或门，即得用与非门实现的全加器，如图2-38所示。

图2-38 用与非门实现的全加器

④将4个一位全加器级联起来构成4位加法器。按图2-21所示的级联关系，将4个一位全加器级联起来即可得到4位加法器逻辑电路图。考虑到最低位做加法运算时无进位输入Ci，所以在设计时，最低位全加器可以按半加器设计，于是按式(2-11)画出S0端的逻辑电路，按式(2-9)中的画出进位输出端Co0的逻辑电路。另外，因为在开关电路的设计时已经说明开关S3同时输入二进制补码的最高位和次高位，所以第四级全加器的A3⊕B3可以和第三级全加器中的A2⊕B2共用。做这些处理不但不影响系统功能，还能节省8个与非门。所设计的具体电路如图2-39所示。

图2-39 基于与非门电路的加法器

3)译码显示电路的设计

该加法器用两个共阴极数码管显示最后的结果。设显示数字的数码管7段分别为a1、b1、c1、d1、e1、f1、g1，显示符号的数码管7段分别为a2、b2、c2、d2、e2、f2、g2。因为输入的数据在-3～+3之间，所以加法器运算的结果在-6～+6之间，其对应的二进制数如表2-17所示，运算后数码管显示的结果如图2-40所示。根据图2-40列出显示结果与其笔画之间关系如表2-17所示。

图2-40 数码管显示效果图

注意：图2-40的二进制补码从左到右分别为S3、S2、S1、S0。

表2-17 数码管显示真值表

根据表2-17画出各笔画的卡诺图，得到最简与或式，再将最简与或式变换为与非式，得数码管各笔画表达式为

注意：其中g2=S3，不需要接与非门，直接连到显示符号的数码管g段。

观察这些逻辑表达式，可以发现有许多与非门可以共用，在设计时将这些与非门分级，再将它们与上一级连接。这样既能节省一些与非门，同时也为电路设计带来方便，也更容易检错。其具体电路如图2-41所示。

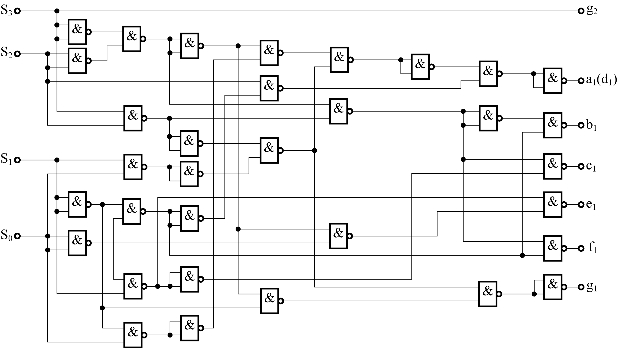
图2-41 译码电路

通过实物测量，译码器输出端电压为5.2V，又因为数码管导通电压为1.7V，为了避免因电流过大而使数码管损坏，还需要加入限流电阻，则限流电阻分到的电压为3.5V，又因为本系统所用的数码管正常工作电流为3mA，所以选用1.1kΩ的限流电阻。其具体电路如图2-42所示。

2.基于译码器的加法器设计

加法运算除了用专用加法器芯片实现外，还可以用二进制译码器74LS138实现。下面介绍用74LS138译码器设计一个一位全加器的方法，设计步骤如下。

(1)根据真值表，写出逻辑函数表达式

根据表2-11，列出逻辑函数表达式如下。

图2-42 译码显示电路

(2)将全加器逻辑表达式等效变形为与非表达式

将A连A2、B连A1、Ci连A0，则S、Co式变为

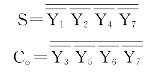
(3)画出全加器的逻辑电路图

根据上式画出所设计的全加器电路图如图2-43所示。

图2-43 基于74LS138的一位全加器逻辑电路