加法器和寄存器的知识链接

1.加法器

在计算机中，所有的算术运算都是通过加法运算完成的。完成加法运算的逻辑器件称为加法器，加法器分为半加器和全加器。

(1)半加器

半加是指在进行加法运算时，不考虑低位的进位，只考虑本位的两个数相加的加法运算。实现半加运算的电路称为半加器。半加器的逻辑电路图和逻辑符号如图2-18所示。图2-18中，A、B为两个二进制数的加数输入端，S为本位和输出端，C为进位信号输出端。

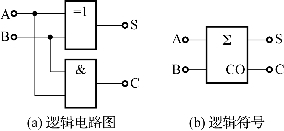
图2-18 半加器的逻辑电路图及逻辑符号

半加器输出端的逻辑函数表达式为

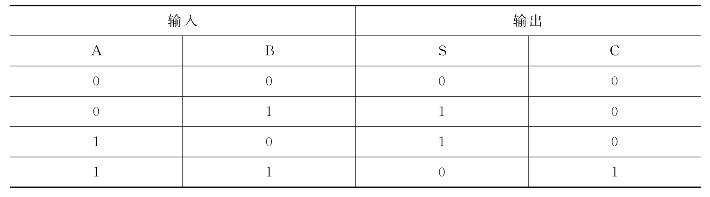
半加器的真值表如表2-10所示。

表2-10 半加器的真值表

(2)全加器

其输入不仅有两个一位二进制数，还有低位送来的进位，能同时进行本位数和相邻低位进位信号加法运算的电路，称为全加器。全加器的逻辑电路图和逻辑符号如图2-19所示。图2-19中，A、B是两个一位二进制加数的输入端，Ci端是低位送来的进位输入端。S端是本位与低位进位之和输出端，Co端是向高位的进位输出端。全加器的逻辑函数表达式为

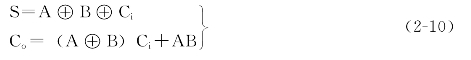
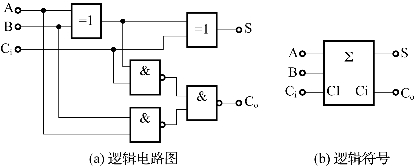
图2-19 全加器的逻辑电路图和逻辑符号

图2-20所示为集成全加器74LS183的引脚排列图，内部集成了两个一位全加器，A、B、Ci是输入端，S和Co是输出端。

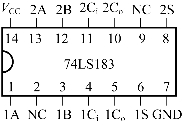
图2-20 74LS183的引脚排列图

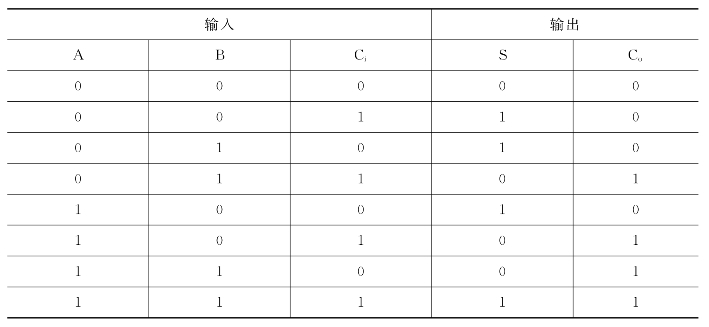
全加器的真值表如表2-11所示。(www.xing528.com)

表2-11 全加器的真值表

(3)多位加法器

一个全加器只能实现两个一位二进制数的加法运算，如果将N个全加器组合起来，就可以实现N位二进制数的加法运算。实现多位二进制数相加运算的电路称为多位加法器。构成多位加法器有串行进位加法器和超前进位加法器两种。

1)串行进位加法器

将N位全加器串联起来，即依次将低位全加器的进位输出端Co接到相邻高位全加器的进位输入端Ci，就构成了N位串行进位加法器。图2-21所示为用4个全加器构成的4位串行进位加法器。

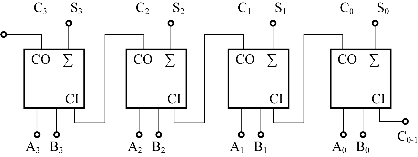
图2-21 4位串行进位加法器

串行进位加法器的逻辑电路简单，但运算速度不快。因为最高位的运算一定要等到所有低位的运算完成，并将进位信号送到后才能进行。所以为提高速度，可以使用超前进位加法器。

2)超前进位加法器

超前进位加法器在做加法运算的同时，利用快速进位电路把各位的进位也算了出来，从而加快了运算速度。常用的集成电路有74LS283和CD4008，这种电路结构复杂，这里不再详细介绍。

2.寄存器

寄存器是数字电路中的一个重要数字部件，具有接收、存放及传送数码的功能。寄存器存入、输出信息的方式可分为并行输入—并行输出方式、串行输入—并行输出方式、串行输入—串行输出方式和并行输入—串行输出方式。

移位寄存器是寄存器中的一类，除了具有存储代码的功能外，还具有移位功能。即可以在移位脉冲的作用下依次左移或右移，实现数据的串行-并行转换、数值的运算及数据处理等。

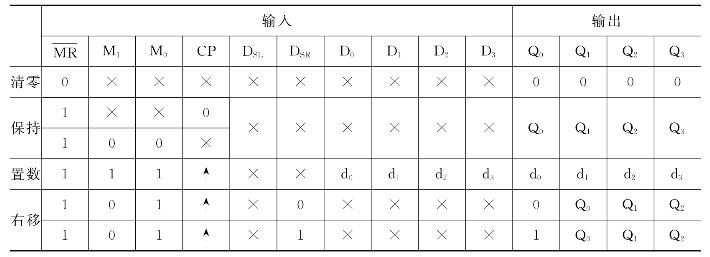
74LS194的引脚图如图2-22所示。图2-22中，D0、D1、D2和D3为并行端，DSR为右移串行输入端，DSL为左移串行输入端，M0、M1为操作模式控制端，Q0、Q1、Q2和Q3为并行数据输出端，为无条件清零端，CP为时钟信号输入端。其功能真值表如表2-12所示。

图2-22 74LS194的引脚图

表2-12 74LS194功能真值表