基于Newtonian本构方程的仿真模拟优化方案

1.基本方程

经典的干法纺丝模型如图4-2 所示，可做以下假设：体系为稳态；纺丝细流为圆形且轴向对称；干法纺丝为一维模型，忽略径向变化；为简化问题，体系为单根纤维。

为描述环化问题，必须对聚酰胺酸的干法纺丝模型进行修正。根据前文所述，环化反应实际上是PAA·2DMAc 络合物失去小分子DMAc 和水形成聚酰亚胺的过程。因此，假定聚酰胺酸纺丝液是由溶质PAA·2DMAc 络合物和溶剂游离DMAc 组成的溶液，在干法纺丝过程中，溶剂DMAc 的挥发服从高分子溶液气液平衡的Flory—Huggins 定律，反应产物水分子的挥发则是由环化反应造成的，也就是说聚酰胺酸的成环反应与脱除络合溶剂过程是同时进行的，产物一旦生成，即挥发完全。这种假设的依据在于DMAc 在聚酰胺酸的干法纺丝中扮演了两种不同的角色，而这两种角色的DMAc 的脱除机理并不相同。

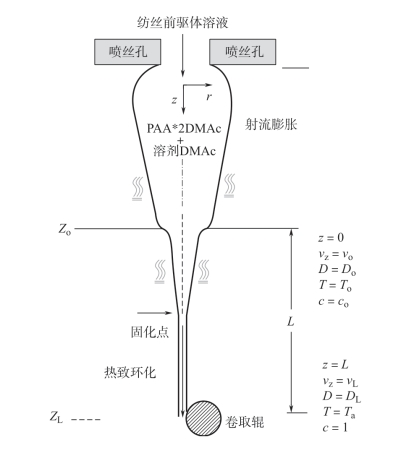
图4-2　干法纺丝成型中聚合物挤出喷丝孔示意图

为描述这个模型，在原来模型的基础上引入环化反应程度这个自变量，即纺丝模型中有DMAc 质量分数ωs（%），细流轴向速度Vz（cm/s），细流平均温度T（℃），细流环化程度β 以及轴向的张应力（τzz - τrr）（N/cm2）这五个变量，联立这五个方程组来求解这五个变量沿纺程z（cm）的变化关系。为减少篇幅，除作者的创新以及需做特殊说明之处，模型中诸多公式都是直接引用过来的，具体可参见文献［3-4，9，12］。

（1）连续性方程：

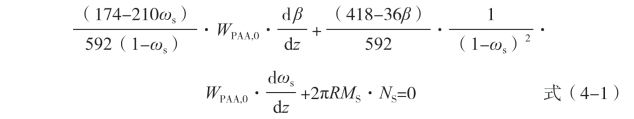
式中：WPAA，0 为质量流量，cm/s；β 为细流环化程度；R 为细流半径（cm）；MS为DMAc 的分子质量（g/mol）；NS 为细流表面溶剂的挥发通量［g/（cm2·s）］。

（2）本构方程：

式中：ηe 为拉伸黏度（Pa·s）。

（3）能量平衡方程：

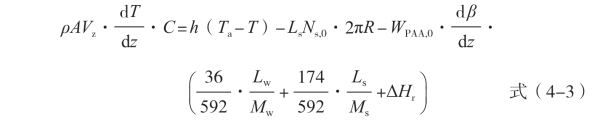
式中：ρ 为细流的密度（g/cm3）；A 为细流的横截面积（cm2）；C 为细流平均比热容［J/（g·k）］；h 为对流热传系数［w/（m2·k）］；Ta 为热空气温度（℃）；Ls 为DMAc 的分子质量（g/mol）；Lw 为水的蒸发潜热（kJ/mol）；Mw 为水的分子质量（g/mol）；ΔHr 为聚酰胺酸环化反应热（J/g）。

（4）动量平衡方程：

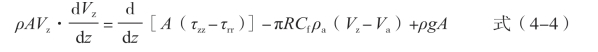
式中：A（τzz - τrr）为轴向应力（N）；Cf 为细流与热空气的摩擦因数之比；ρa为热空气密度（g/cm3）；Va 为热风速度（cm/s）；g 为重力加速度（m/s2）。

（5）环化方程：

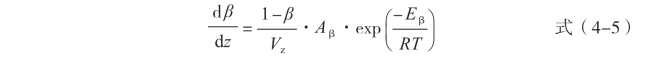
式中：Aβ 为指前因子（s-1）；Eβ 为表现反应活化能（kJ/mol）。

2.模拟的初始值

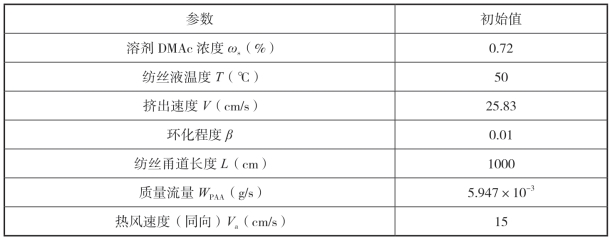
基于PAA/DMAc 溶液体系的成型过程，其主要参数见表4-1。

表4-1　干法纺丝模型的初始参数

(www.xing528.com)

3.热风温度对环化程度的影响

根据以上模型对聚酰胺酸纤维成型过程进行模拟预测，重点讨论部分工艺参数对环化程度的影响。固定初始张应力为33.4×10-5 N（即对应Vz = 500 cm/s 时的初始应力），本构关系采用Newtonian 方程，环化参数采用第二种快速反应方程，而改变热风温度来考察这几个自变量随纺程的变化。

图4-3 比较了溶剂含量ωs 和轴向速度Vz 在不同热风温度下的变化情况，由图可以看出，热风温度越高，固化越快，与聚酰胺酸络合的DMAc 挥发得也就越快，并导致最终的平衡轴向速度越来越低的方向移动。这是由于轴向张应力对轴向速度在高温下所起加速作用的时间越来越短所造成的，这也可以从热风温度越高，达到最终平衡速度的点越来越靠近起始点这一现象得到验证。

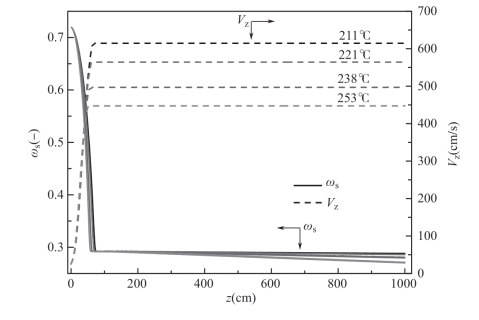
图4-3　热风温度对溶剂含量和轴向速度的影响

图4-4 则显示了细流温度T 和环化程度β 在不同热风温度下的变化情况。可以看出，热风温度越高，固化速度越快，细流达到热风温度的时间也越短。仔细观察还可以发现，热风温度越高，固化前细流经历的温度平台也越来越高，这说明聚酰胺酸与热风的热交换效率也越来越高，解释了在本次模拟中固化前温度没有经历一个下降的过程的原因。对于环化程度来讲，热风温度越高，环化程度越高。经过前面的对比发现，这是由两个方面造成的，一方面，热风温度越高，细流固化后能达到的温度也越高，加快了环化反应速率；另一方面，由于热风温度越高，平衡时的轴向速度却越低，延长了细流在高温下的停留时间从而增加环化程度。当热风温度达到253℃时，模拟预测的环化程度能达到12%，更加接近实验测得的环化程度。

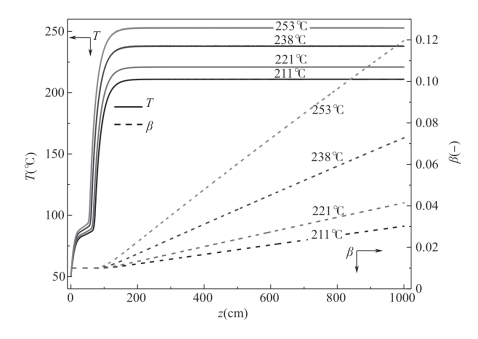
图4-4　热风温度对细流温度和环化程度的影响

4.本构方程对环化程度的影响

Newtonian 方程是描述聚合物溶液流体最简单的方程，它指出流体的形变速率梯度与张应力成正比，而与流体形变中的黏滞阻力（黏度）成反比。本构方程确定了张应力和细流形变或者说细流轴向速度之间的关系。图4-5显示了Newtonian 方程与White-Metzner 方程对自变量A（τzz - τrr）和Vz 的影响。由图4-5 可以看出，在固化前，这两个方程对张应力和轴向速度都没有太大影响。固化后，对于平衡时的轴向速度Vz 而言，White-Metzner 方程要低一点，不过差别很小，没有实质性的影响。White-Metzner 方法计算的平衡轴向速度低，在于其考虑了聚合物弹性效应的影响，固化后，虽然黏度迅速上升近至无穷大，但松弛时间是黏度的函数，它也会迅速上升而抵销一部分黏度的影响。这个原理也同样适用于本构方程对张应力A（τzz - τrr）的影响。

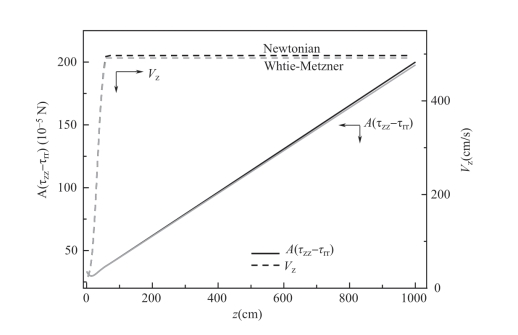
图4-5　本构方程的选择对轴向应力和轴向速度的影响

从图4-6 可以看出，本构方程对DMAc 含量随纺程的变化几乎没有影响，这是因为固化前DMAc 含量的变化主要取决于温度和初始张应力，与本构方程的选择关系不大；而固化后，本构方程对DMAc 的含量只有非常有限的影响，这种影响也是由于本构方程的选择对平衡时的轴向速度的间接影响造成的。通过环化程度的变化看出，固化后采用White-Metzner 方程计算方法得到的环化程度比Newtonian 方法略高。

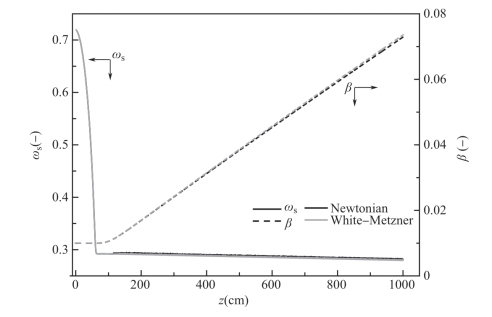
图4-6　本构方程的选择对溶剂含量和环化程度的影响

以上分析可见，本构方程的选择对于干法纺丝模拟影响并不大，无论是Newtonian 方程，还是White-Metzner 方程，在描述聚合物溶液细流张应力和形变速率的问题上，它们都是一种宏观上的模型，对于预测聚合物流体行为都只能近似地表达出某种宏观上的关系。

5.环化参数对环化程度的影响

环化反应参数（主要指环化反应动力学的指前因子Aβ 和表观反应活化能Eβ）对最终纤维环化程度的影响如图4-7 所示，该图显示了不同环化参数对DMAc 含量与轴向速度的影响。对于轴向速度而言，只要其他初始变量一致，采用不同的环化参数对轴向速度没有任何影响。也就是说干法纺丝中，轴向速度以及张应力与聚酰胺酸是否发生环化并无关系。而对于DMAc含量而言，固化前环化反应对溶剂DMAc 的挥发也没有影响，固化后环化反应是通过络合DMAc 的脱除来影响DMAc 在纺丝细流中的含量的。

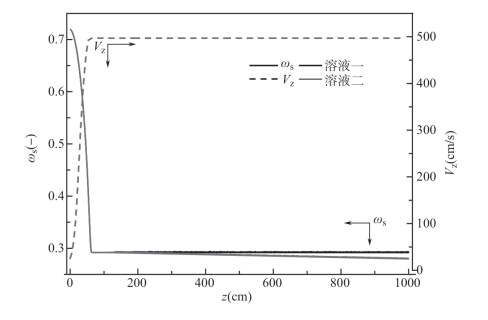
图4-7　环化参数对溶剂含量和轴向速度的影响

图4-8 进一步说明上述问题，由之前的分析可知，环化参数的选择对张应力和轴向速度都没有影响，也不会对纺丝细流的温度造成影响；也就是说，当纺丝细流温度达到热风温度之后，由于环化造成的小分子的挥发吸热会很快从热风中得到补偿，不会影响纺丝细流的温度。由于温度和反应时间变化一致（轴向速度一致），可以看到环化参数对环化程度没有明显影响，采用第一种环化参数计算得到的环化程度几乎没有任何变化（＜1%），而采用第二种环化参数纺丝细流在甬道中发生的环化程度高达7%左右，比之前预测的要高出很多，且与实测值更为接近。

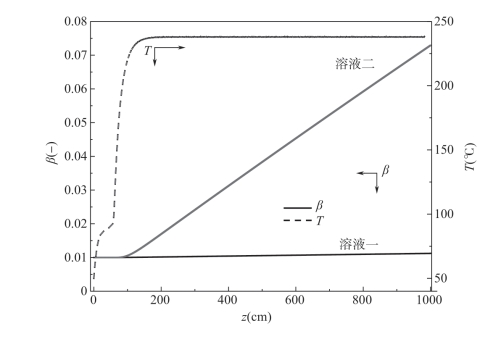
图4-8　环化参数对细流温度和环化程度的影响

尽管如此，该模型与纺丝实验中测得的实际环化程度仍有较大的差距，由于在Newtonian 模型的本构方程仅仅用零切黏度将轴向速度与拉伸应力联系起来，不能反映其他微观参数（如高拉伸应变）对环化的影响。因此，寻找其他本构模型来研究聚酰胺酸的干法纺丝过程中的影响因素是非常必要的。