卧式分离容器的优化分离数据设计

卧式分离容器是如何进行设计的？在欧美国家，产品设计各自有不同的计算方法，这里根据笔者的理解，介绍其中一种较常用的分离的计算方法。

首先是确定分离液滴直径，参考文献[7]对制冷剂的液滴直径统一规定为d^∗=0.00152m。为了对U_T值进行测试，研究人员在这方面进行了大量的工作。根据参考文献[7]的数据披露，从1955年到1993年，先后有19位学者进行了这方面的研究，并且得出了许多有意义的数据。

图8-16是从参考文献[3]中选取的一张低压循环桶图，下面进行计算。

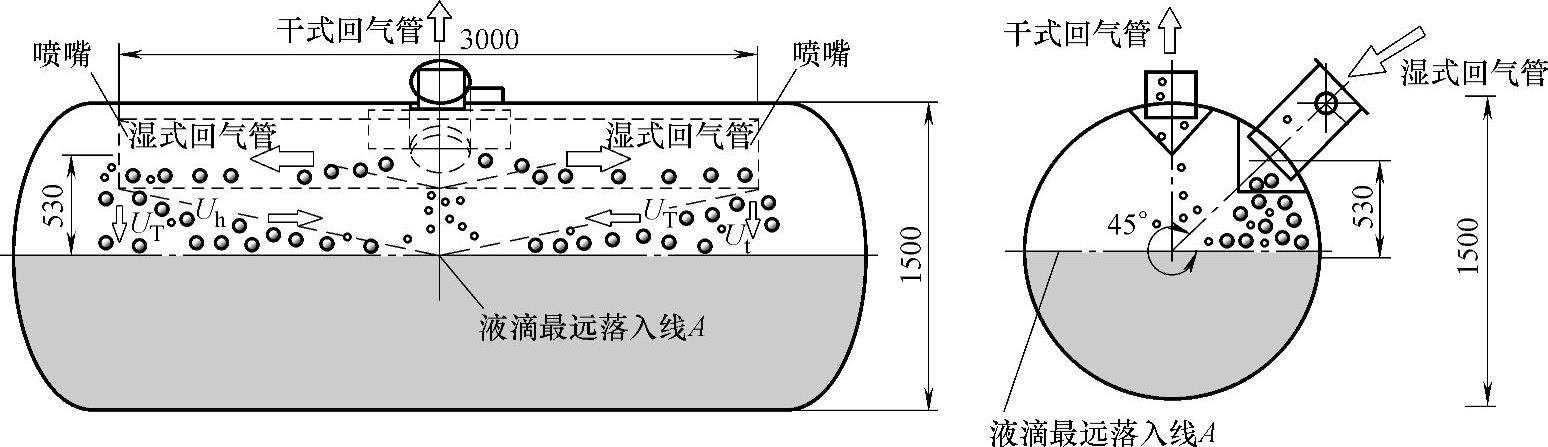
图8-16 卧式分离容器的分离计算图

U_T——分离液滴向下运动的终端速度（m/s）；

U_h——分离液滴水平运动的速度（m/s）；

1/2L——两根湿式回气管距离的1/2（m）；

h——湿式回气进入容器的喷嘴中心线到运行液面的高度（m）；

D——容器直径（m）。

计算的过程：先求出分离液滴向下运动的终端速度U_T（m/s）。

U_T=K_s[（ρ_L-ρ_g）/ρ_g]^0.5 （8-48）

式中 ρ_L——制冷剂液体密度（kg/m³）；

ρ_g——制冷剂气体密度（kg/m³）；

K_s——要么是常数，要么取决于一个或多个变量的速度值（m/s）。

K_s=k′[（ρ_L-ρ_g）ρ_g]^0.328 （8-49）

其中，k′=0.00272m/s（k′值在-40～0℃时，对于R22和氨是0.021～0.075m/s）。

两个公式合并得：

U_T=0.00272×[（ρ_L-ρ_g）ρ_g]^0.328×[（ρ_L-ρ_g）/ρ_g]^0.5 （8-50）

式（8-49）中的K_s值，也可以通过图8-17中制冷剂的表面张力与垂直分离距离来查找得出。

一般情况下，容器最大液面高度会采用1/2D（容器的中线位置，但是也有采用D×60%的高度）；容器的回气管一般有两个进气口进入容器，目的是使容器直径可以变得更小、长度更长，降低制造成本。

再根据U_T计算分离液滴横向运动的速度U_h。它们之间的关系是：

U_h=（1～5）U_T （8-51）

式（8-51）的意思是，系数从1～5，表示U_h只可以大于或者等于U_T，至于这个系数选择多大，取决于生产厂家的设计人员对安全系数的把握，一般会取3左右。这种K_s的计算在参考文献[7]也列举了许多论文与实验值，不同的制冷剂K_s值U_h也不同，因此不同的生产厂家计算的结果会有一些差异。将分离液滴水平运动的速度U_h计算出来，那么容器的分离能力计算也就解决了。这种U_h的计算方法，根据参考文献[6，7]的介绍，最高控制液面可以达到容器直径2/3的位置（与喷嘴高度设置有关），而水平距离分离液滴的运行时间控制在3s以内。这种容器设计一般规模比较小，而且是根据工程提供的数据设计。因此在工业制冷规模比较大的容器中，水平距离分离液滴的运行时间可能达到6s以上（一些二氧化碳制冷系统甚至超过10s）。

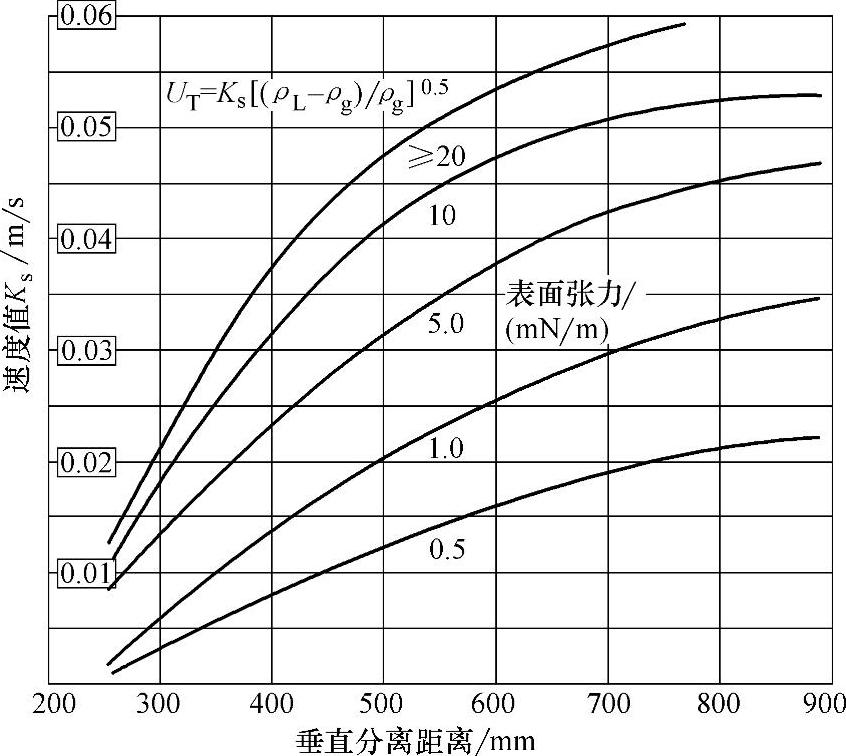
图8-17 计算分离液滴的水平速度系数值K_s/（m/s）

参考文献[7]提供了一些常用的在容器中垂直速度与夹带速度的参考值（制冷剂液滴直径为0.00152m），见表8-6。

表8-6 气液分离器的设计数据^[7]（液滴设定值0.00152m）

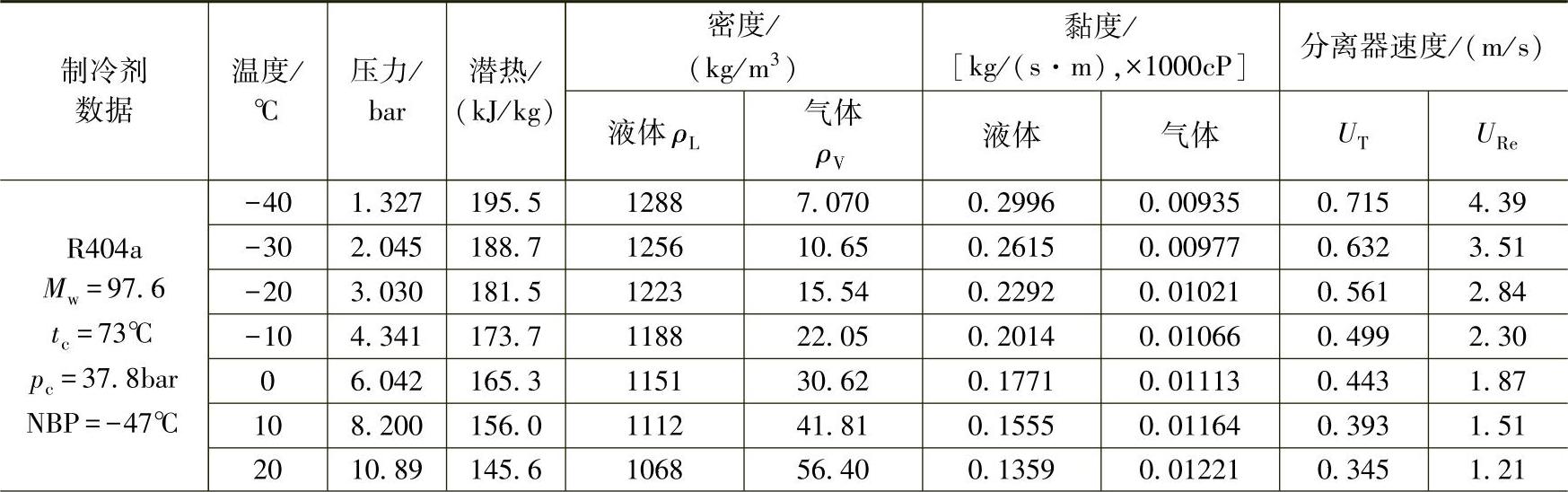
（续）

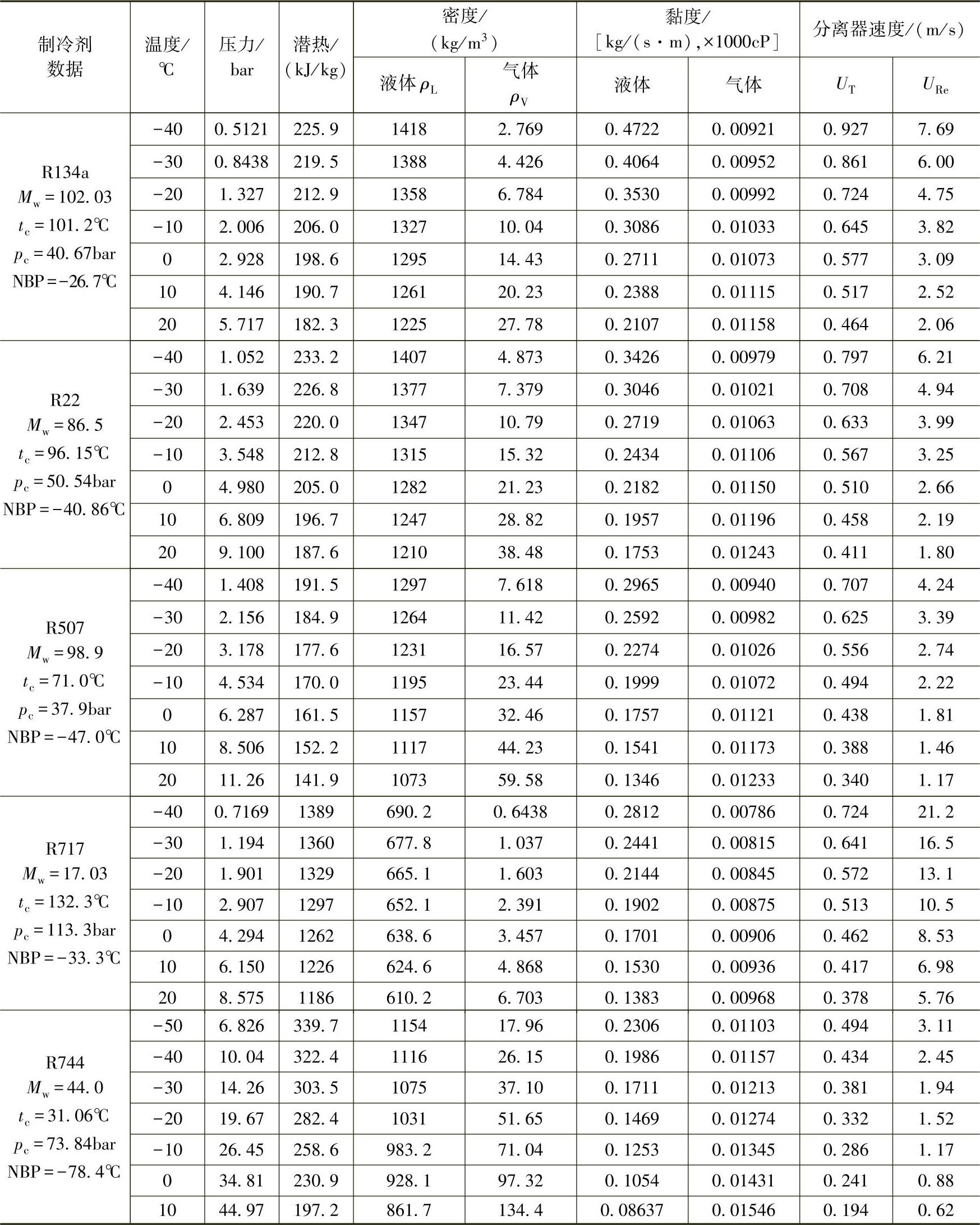
注：M_w——摩尔质量；

t_c——临界温度；

p_c——临界压力；

NBP——沸腾温度；

U_Re——再夹带速度（m/s）。

1Pa·s=1000cP。

1kg/（m·s）=1Pa·s。

表8-6中，不同制冷剂在不同的蒸发温度下的阻力系数是变化的，为了方便以后在选型计算时能够更快得出结果，笔者把这些阻力系数C_D值整理成图形（图8-18），供读者在容器选型时参考。

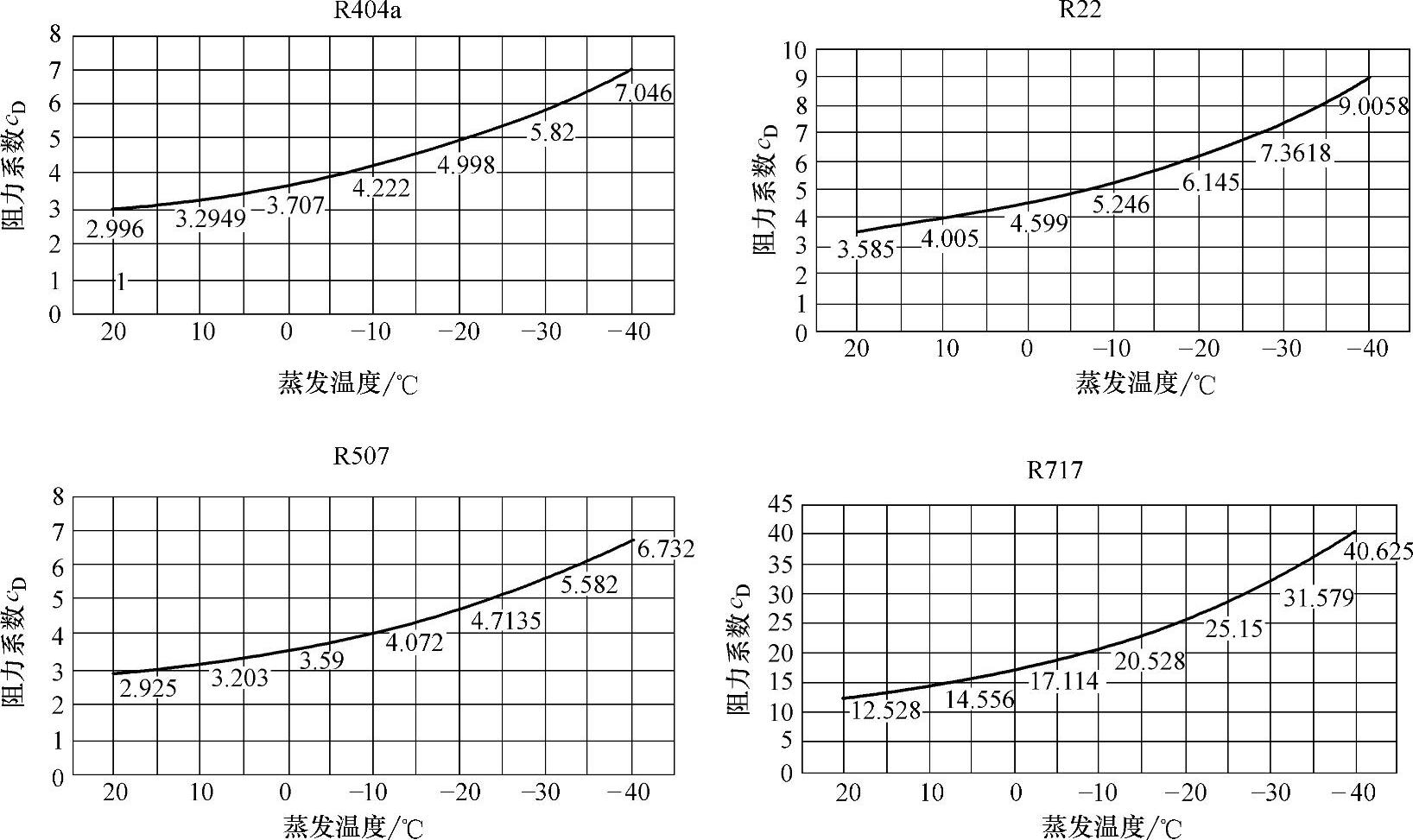
图8-18 各种制冷剂在不同蒸发温度下的阻力系数

这种选择方式的原理是：不同制冷剂在蒸发温度发生改变时，分离液滴在容器的气体区域中移动所遇到的阻力系数（雷诺数）是不同的。蒸发温度越低，阻力系数越大（制冷剂液体的黏度也增大），这是一种计算模式。

【例8-3】 若在图8-16中的卧式分离容器中采用氨作为制冷工质，容器的尺寸如图8-16所示，h=0.53m，L=3m，容器直径D=1.5m。当蒸发温度为0℃、供液温度在35℃时，这台卧式分离容器允许的分离速度（容器的运行液面在容器容量的50%）是多少？

解：查附录三，氨在0℃时气体焓值是1460.66kJ/kg，气体比体积是0.289m³/kg，液体比体积是1.5659dm³/kg，+35℃时的液体焓值是362.58kJ/kg，气体焓值是1487.65kJ/kg。垂直速U_T，可以用式（8-11）计算。这时，根据参考文献[7]提供的数据，雷诺数选择大于1而小于30之间的插值。在图8-18中查得对应的阻力系数C_D是17.114，即

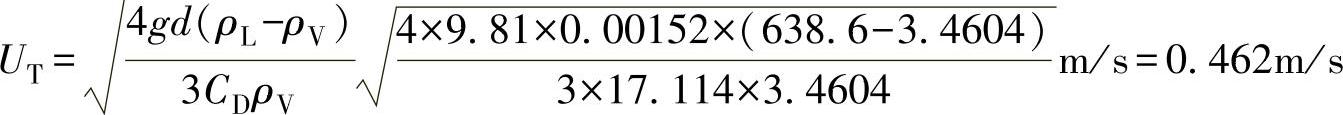
这个值就是表8-6中数据的计算依据。

也可以通过查图8-18得出的数据来计算。由于氨在0℃时的液体张力＞20mN/m，这时垂直分离距离是530mm，在液体张力≥20mN/m的曲线上，对应的K_s值约为0.05m/s。再把这个数值代入式（8-48），即可计算出液滴的垂直下降速度U_T。

把U_T代入式（8-51），得液滴水平速度：

U_h=3U_T=3×0.462m/s=1.386m/s

以上是把参考文献[6，7]的一些卧式分离容器的公式汇集后整理的计算过程，这种理论在国外还是有一定的市场的。但是笔者通过对参考文献[2，3]与[15]相关数据的追踪，发现用不同方法得到的数值还是有相当大的偏差。最主要的问题是在卧式分离容器中，液滴的垂直下降速度U_T的计算。在参考文献[6，7]中U_T是一个定值，由这个定值来推导卧式分离容器中液滴的水平速度U_h，但实际上U_T在卧式分离容器中是一个变量。以下观点是笔者通过物理现象以及相关数据，反复推敲得出的理论与计算依据，仅代表个人观点。

在立式分离容器中，液滴的下落速度计算建立在三种合力的理论推导之上。这三种合力的运动方向是相互垂直的，而其中有一种力F_D，被定义为作用在液滴垂直向上的力，是牵引力（在实际中可以理解为压缩机在立式分离容器中的吸气作用力）。但是这种力在卧式容器中已经发生方向性的改变，已经变成水平方向的作用力。因此，原来的计算公式推导必须做出相应的修正。

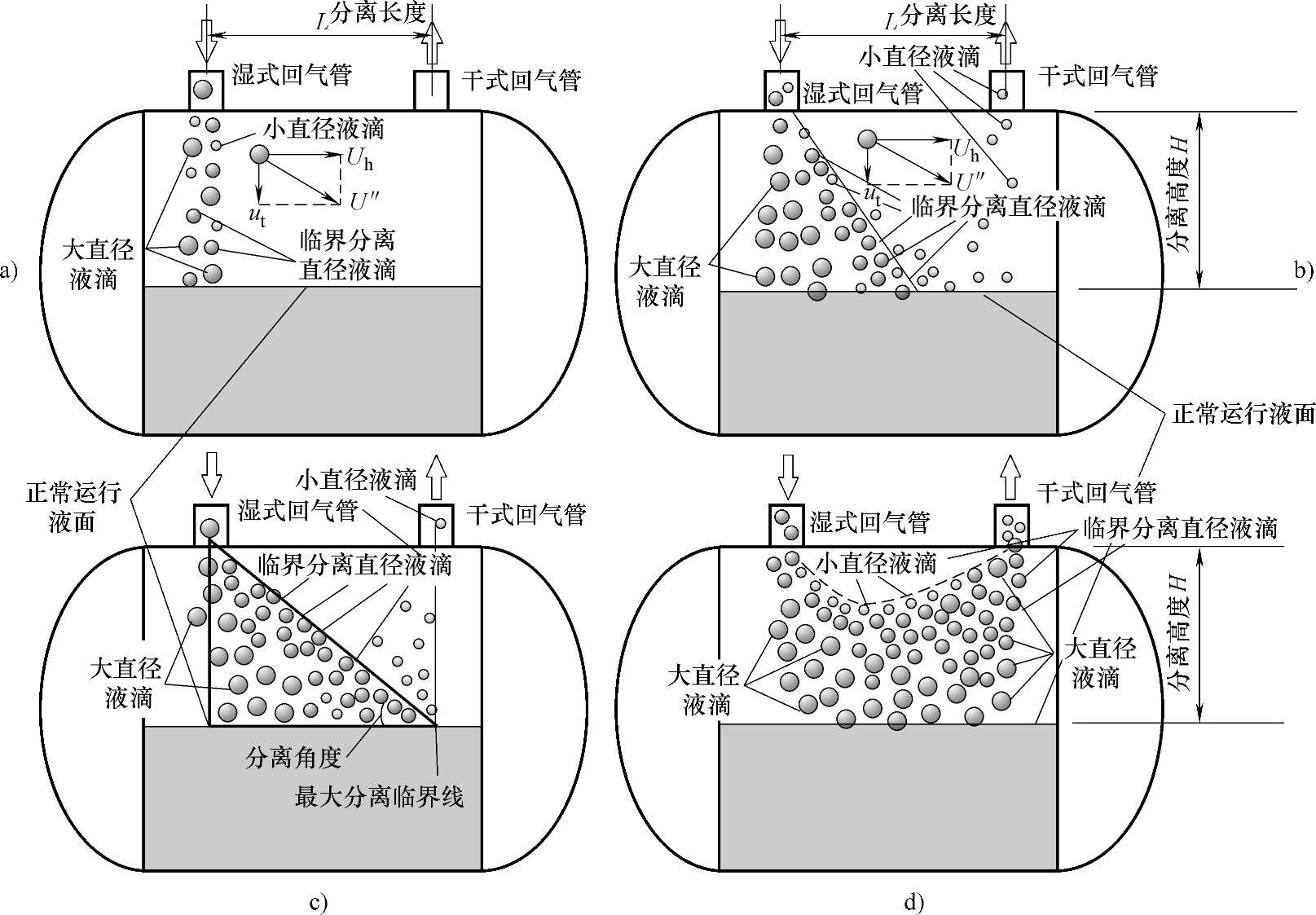
图8-19 制冷剂在卧式分离容器中分离的各种状态

图8-19是笔者对这种理论的一种解释，容器的运行液面在容器容量的50%。图a为静止状态，压缩机没有运行，分离液滴垂直向下，分离液滴的垂直速度U_T不变，水平速度U_h=0；图b压缩机开始运行，液滴垂直速度U_T由于水平作用力的影响开始改变，水平速度U_h开始增大，但没有超出设计的分离速度，分离液滴在两种力的作用下斜向进入容器运行液面，实现分离。分离液滴这种斜向运动的轨迹，可以理解为由两种方向作用力的合力所产生；图c压缩机加大吸气能力，液滴垂直速度U_T变得更慢，水平速度U_h达到最大设计的分离速度，特点是临界直径的分离液滴斜插，达到容器水平位置的最大分离临界线，这时也称为容器在该工况下的最大分离能力；图d压缩机再加大吸气能力，临界直径的分离液滴垂直速度U_T已经改变了方向（在压缩机的牵引力作用下），需要分离的液滴可能向着干式回气管的出口方向运动，并有可能不下落而直接被压缩机吸走。水平速度U_h超过最大设计的分离速度，部分液滴会被压缩机吸入，造成液击。

这种分离方式可以比喻为一只正在某个高度飞翔的风筝突然断线，而分离的液滴就好像是这只突然断线的风筝。由于断线的原因，风筝从一个相对静止的状态在重力、空气浮力以及横向风力的作用下向地面的某个指定的方向飘落。若重力与空气浮力不发生变化，风筝飘落到地面的水平距离取决于横向风力的大小。风筝飘落到地面后，若还没有到达指定位置，表示分离过程完成；如果风筝飘落到地面时刚好到达指定位置，这种横向风力的速度（水平分离速度）可以比喻为卧式容器最大的分离速度。大于这个速度，风筝已经超越指定位置还没有飘落到地面，表示没有实现分离。从这里可以推论，相对地面的下落速度的绝对值受到水平拖曳力大小的影响（与U_T有关）。在分离高度确定后，如果按以上的推论，垂直速度U_T不变，那么水平拖曳力再大，液滴下落的时间也不会变化。但是一个下落的风筝，有横向风与没有风到达地面的时间是不一样的。那是因为即使以相同的速度运行，在相同高度下垂直的距离与斜向运动的绝对距离是有差别的。那显然参考文献[7]的理论与这种物理现象是矛盾的。

从图8-19可以看到整个制冷剂液滴的分离过程变化。要实现制冷剂液滴分离的最大化，也就是要使得制冷剂液滴进入容器运行液面时，水平距离最远不能超过容器的最大分离临界线。这条最大分离临界线的基本定义可分两种情况。

一种情况是，图8-19中，是单根湿式回气管进入容器，单根干式回气管离开容器，运行液面一般定义为容器的中线位置（一半的液体容积），另一条线为干式回气管中心线与液面的相交线（图8-19c），计算公式是：

h/U_T=L/U_h （8-52）

式（8-52）的意思是：分离液滴要到达最大分离速度的位置，液滴在垂直方向到达液面的时间，与在水平方向到达出气口的中心，垂直线与液面交点的位置时间相等。

在容器设计中，h与L都由生产厂家设定，U_T可以用理论公式与实验数据进行测定。前面已经提过U_T的理论公式（8-11），但是在卧式容器计算中，这个公式需要重新修订，那么在容器设计时所需要的U_h值就不难求出了。

另一种情况是两根湿式回气管进入容器，单根干式回气管离开容器，如图8-16所示。这种情况在实际应用中最为普遍，运行液面也定义为容器的中线位置（一半的液体容积），另一条线为两根湿式回气管中心线与液面的相交线A，计算公式是：

h/U_T=L/2U_h （8-53）

式（8-53）的意思是：当制冷剂需要分离的液滴在垂直方向达到最高运行液面时，分离的液滴在容器的水平方向上，也同时到达容器的长度方向的中线A上。这种情况，在外资的制冷容器选型软件上称为在该工况下容器运行的最大制冷量（Max Capacity）以及最大速度（Max Velocity）。当水平分离液滴速度超过最大值，就可能会使系统产生液击。

在卧式分离容器中，分离液滴在容器内的运动在物理上解释是一种抛物线运动。而出于数学计算，可以认为是如图8-20中由重力与水平牵引力共同作用下构成三角形的斜边向下运动。由于牵引力方向的改变，需要对液滴下落速度的式（8-11）进行修正。在式（8-52）与式（8-53）中，只有修正了液滴下落速度（绝对值），才可能计算出液滴的水平速度。这种修正与容器内部的结构有密切的联系，从图8-19c中可以看到，湿式回气管中心进口（线）点、最大分离临界线、运行液面构成了一个直角三角形的分离角度θ，即tanθ=h/L（分离高度与分离长度之比）。从数学以及合力的角度分析，这个分离角度越小，tanθ的值就越小，需要的水平速度越大（分离角度越小意味着垂直分离速度的绝对值变小的趋势）。也就是说，分离长度长有利于分离速度加快。但同时，液滴下落的速度也会降低。因此在设计分离容器时，确定容器的直径后尽量把分离长度延长一些，也就是使tanθ的角度小一些。一般不会设计成tanθ≥45°，否则其数值会≥1，分离距离减小，显然不利于液滴的分离。

但是tanθ也不能太小，太小会产生另一个问题，就是再夹带速度问题。这个问题在文章的下一节会详细解释。

那么受水平拖曳力影响的液滴下落计算速度U_T1（这里把这个数据称为卧式容器的液滴下落计算速度，或者称为液滴下落的绝对值速度）与水平速度U_h的关系是：U_h=0，U_T1是自由落体运动在垂直方向绝对值速度；U_h越大，U_T1越小。与式（8-11）的U_T比较（图8-19），它们的关系是：

U_T1=ftanθU_T=（H/L）fU_T （8-54）

式中 f——修正值。一般为了方便计算，容器直径小于1.35m时，f=1.0（自定义）；容器

直径≥1.35m时，f=1.13（自定义）；如果直径

大于2.4m，还需要进行修正。(www.xing528.com)

在图8-20中，U_h=0，U_T1是自由落体运动；当U_h速度加大并且趋于U∗的时候，U_T1逐渐变小而且趋于0。这个时候指定分离直径的液滴就好像一粒刚刚出膛的子弹，在一段并不太长的距离内，水平直线运行，而垂直下落速度接近零。出现这种情况时，指定分离直径的液滴不能分离或者产生再夹带速度，把运行液面中的一些液滴重新带走。

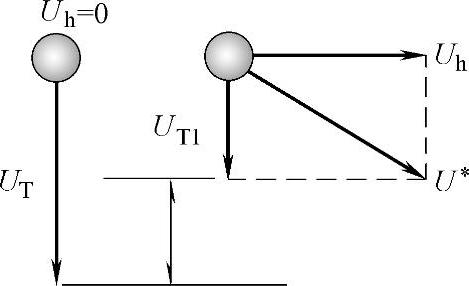
图8-20 U_T1与U_T的比较

还是以【例8-3】的题目为例进行这种方法的计算，这里采用的是工业制冷的计算方法，分离液滴直径=0.003m，C_D=29，代入式 （8-11）：

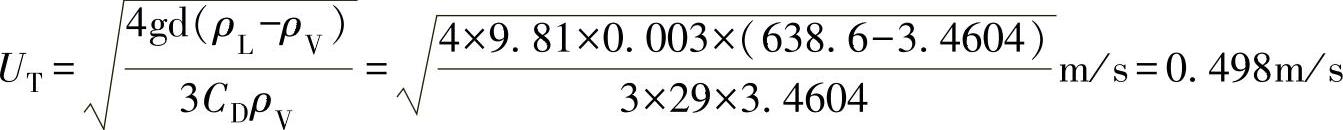
将U_T=0.49m/s代入式（8-54），得

U_T1=（h/0.5）fU_T=（0.53/1.5）×1.13×0.498m/s=0.2m/s

再将U_T1=0.2m/s代入式（8-53），式中的U_T用U_T1代替，即

h/U_T1=1/2L÷U_h，0.53/0.2=1.5/U_h，

得U_h=0.56m/s

对比两种计算方法后发现，差别还是比较大的。

以上的计算似乎又回到了类似于立式分离容器的最大垂直分离速度的计算方式，因为从式（8-52）或者式（8-53）可以简化为

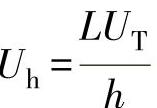(8-52a)

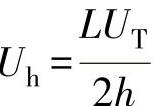(8-53a)

把式（8-54）相关系数代入，以上两个公式都变成：

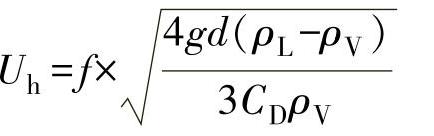(8-55)

式（8-55）是分离角度θ在最终计算上没有体现，但是，tanθ的函数值表示tanθ＜45°的道理。而分离长度与分离高度之间的关系也体现了tanθ的函数关系。之所以这样举例，是笔者对这种分离过程的一种理解。另外需要强调的是湿式回气管与最高运行液面的垂直距离H₃，其最小不能少于0.25m。

这种计算是建立在低压循环桶的湿式回气管与干式回气管，相互间处于一种固定位置的状态下。如图8-21所示，图的左边剖视是参考文献[2]的产品，而右边剖视是参考文献[15]的产品；图8-16是参考文献[3]的产品。它们的共同特点是，干式回气管与液面的中心线垂直；而湿式回气管与液面成45°角。在平面图（图8-16）上，湿式回气管分成两边进入循环桶内。这些产品的生产厂家都是国际上一些最著名的设备制造商，它们的产品数据值得参考。

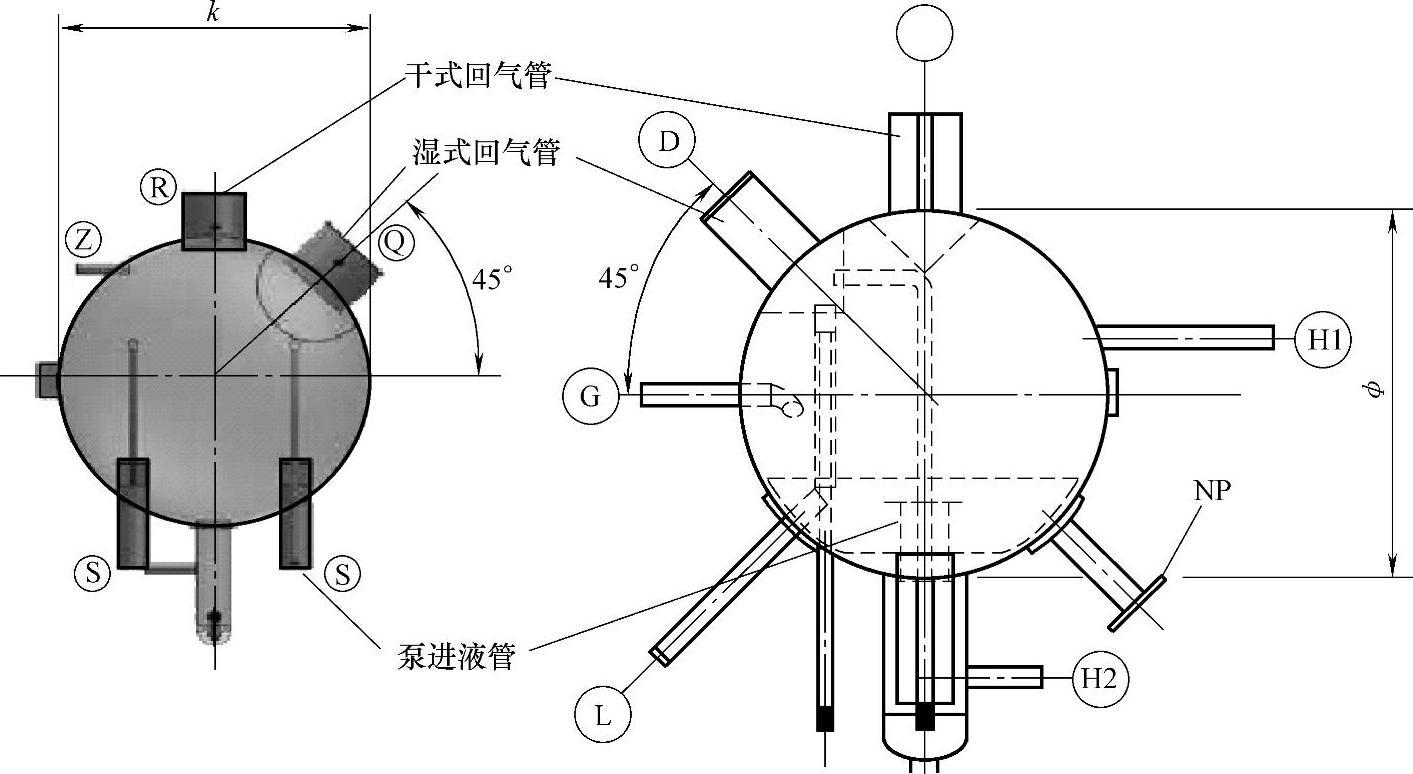
图8-21 低压循环桶剖视图（湿式回气管与干式回气管的相互关系）

这种分离容器的一些设计特点是：容器的进气是一根总管，进入容器后分成两根管（等边角钢或者半圆，见剖视图），在接近容器的封头位置才让气体进入容器。分离后的气体集中在容器顶部的回气总管回到压缩机。若将与容器长度平行的进气管长度设定为L，并设这根管的底线与容器的运行液面（容器容量的一半位置）之间的距离为h，那么这两者的关系笔者认为是：h＜1/2L（这里设定容器的有效长度在3m左右），因此容器的半径一般不超过1.8m。这是为了让分离液滴尽快地落入到运行液面，完成分离，同时希望分离液滴的水平速度不要太快。这也证明了卧式容器中水平的分离距离越长，分离能力越强的特点。另外一个特点是：容器的最高运行液面一般不能超过50%。原因是这些容器的湿式回气管口设计得比较低（与参考文献[6，7]中的设置高度有区别），如果把最高运行液面提高，容器的分离高度是湿式回气在容器内的水平中心线与最高运行液面的高度差。美国相关公司通常是采用容器水平中心线（50%）为最高运行液面；而欧洲部分公司的卧式容器会把这条最高运行液面线提高到容器水平高度的65%～72%之间。但是容器内部结构的布置与美国的公司不同。

笔者在本书中的计算方法主要采用的是以美国相关公司的计算方法为主，包括第10章的例题都是以美国相关公司的容器作为计算依据。而欧洲部分公司的卧式容器计算相对比较复杂，主要是缓冲容积的计算。与缓冲容积计算相关的最高运行液面水平高度按65%～72%的容积计算，比按50%的容积计算要复杂一些。但是，这种设计的最大优点是增大了容器的缓冲容积。另外，欧洲公司把稳定容积计算称为启动容积（Start-up Volume），通常是以制冷剂泵的单位时间内的流量容积（L）计算，一般是1～3min泵的流量（Time for Pump）。

为什么湿式回气管与液面成45°角？这主要是从湿式回气管与干式回气管进入容器的角度考虑。对于低压循环桶，这两种管一般是从容器的上方进入。由于湿式回气管进入容器后分成两边伸延，必然与干式回气管的位置发生冲突。为了解决这些问题，45°无疑是比较理想的角度。虽然这样做会牺牲一些分离的高度，但从理论分析可以知道，水平拖曳力是影响液滴下落速度的主要原因。数据表明如果湿式回气管偏离一些距离，水平拖曳力对液滴下落速度的影响会减少，即液滴下落速度会加快，有利于液滴的分离。但是在容器内如果偏离太多，分离高度又减少了。这就是在低压循环桶的容器内广泛采用上述布置形式的原因。

讨论到这里，可能有读者会问，为什么卧式气液分离器又不采用这种布置形式了呢？这也与湿式回气管与干式回气管进入卧式气液分离器的位置有关。一般这种分离器使用的蒸发器一般在容器的下方（如冷库的冷风机或者板式换热器），湿式回气管可以设计为在容器的下方进入更加合适，这样连接阻力就减小了。因此，湿式回气管与干式回气管可以在同一个平面上（图8-23）。还有气液分离器在设计计算中不必考虑缓冲容积的存在（除非该容器同时兼顾贮存排液功能），分离高度就是湿式回气管的中心线与运行液面的高度差（运行液面的高度不是一半的容积的高度，一般是距离容器底部105～110mm）。

从以上计算可以知道，容器的内部尺寸、分离方式（增加挡板、除雾器等）和容器的形状，每一个尺寸的变化都会使分离能力（制冷量）发生改变，这是在容器设计时需要重视的。另外，这里采用半圆面积进行计算，也是假设容器内部没有任何管径、挡板之类的物体。在实际计算中与立式分离容器一样，需要考虑这些元件的存在，即要用半圆面积减去这些元件的截面面积。

根据笔者查到的资料，卧式低压循环桶的生产厂家设计类型一般分成两种。一种是不管容器直径多大，其容器长度（不考虑两边的封头长度）都没有变化。如Frick公司、H.A.Phillips&Co、EVAPCO.Inc USA等都采用这种设计，容器有效长度一般在2997～3048mm范围内^[15，2]。由于不同的厂家使用不同的数据计算方法（内部布置也不尽相同），计算的结果与上面的计算会有一些区别。

由于上述原因，卧式分离容器的制冷量随着容器内部的尺寸变化而改变，这一点与立式分离容器不同。立式分离容器的计算完全是理论计算，只要容器的最高液面与进气管以及回气管保持足够的高度（这种高度可以认为是安全高度），再将理论分离速度乘以0.75～0.9，而容器的其他尺寸与计算没有直接的关系。卧式分离容器的分离速度与分离容器直径有关（直径大的需要修正）。

图8-19的单边分离方式与图8-16的双边分离方式有什么区别呢？从【例8-3】的计算中可以知道，双边分离方式的其中一边最大分离速度是0.56m/s。如果这台容器的半径比较小，这种较高速的分离速度可能会使压缩气体把运行液面的一些液滴重新带起来（这种现象称为再夹带，夹带的意思是指在气体气流中，液滴以重力形式传递或携带），通过回气管进入压缩机，造成液击。在英文的论文中把这种现象称为The Re-entrainment Velocity（再夹带速度）。这种现象通常发生在比较细长的分离容器中。另外在复核卧式容器的水平速度时，需要把再夹带速度值作为一个指标，检查计算的水平速度是否超过再夹带速度（用U_Re表示）。

图8-22是解析在水力直径d_hl内液体流动产生液滴的再夹带速度的各种条件，即

d_hl=4A/P （基本原则）

d_hl=D（L_h=D或者D/2）

d_hl=1.2D（L_h=0.75D）

d_hl=0.6D（L_h=0.25D）

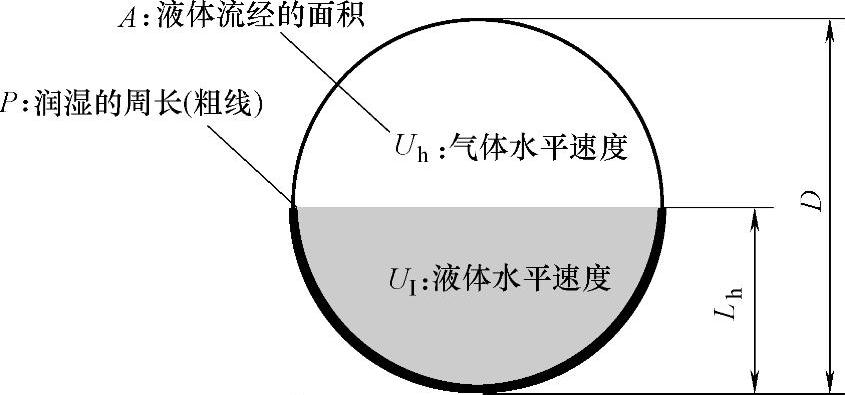
图8-22 液体在水力直径d_h1圆管中流动

D—圆管的直径 L_h—圆管中液体的高度

液体的雷诺数：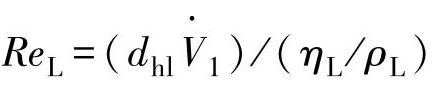

液体的密度系数：Rρ=（ρ_L/ρ_g）^0.5

界面黏度： N=η_L（ρ_Lσ）-0.5[（ρ_L-ρ_g）g/σ]^0.25

式中 _ηL——液体动态黏度[kg/（m·s）]；

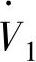——气体流量（m³/s）；

ρ_L——液体密度（kg/m³）；

ρ_g——气体密度（kg/m³）；

σ——气-液表面张力（N/m）。

这种再夹带速度的计算，根据不同的雷诺数与界面黏度范围，有不同的计算方式（表8-7）。

表8-7 再夹带速度的计算

公式D与E，只有当运行液面高度L_h≤0.75D时，才需要进行这种计算。各种制冷剂不同温度的再夹带速度U_Re在表8-12中列出。

【例8-3】的计算结果U_h=0.56m/s，与表8-6中氨在0℃时的再夹带速度U_Re=8.53m/s比较，还是相当安全的。

笔者认为，之所以把长度L确定在2.9～3m，另一个原因是考虑运输车辆的长度以及运输高度。这些容器通常体积较大，但是却不是很重。即使是直径在2m左右的容器，一台普通的货车就可以满足装运需要。这种长度的设计使容器恰好能用普通货车装上，这是从经济的角度考虑。

但是这种尺寸比例的卧式分离容器也有一些缺点，主要缺点是这种容器的分离能力与它提供的缓冲容积不成比例。在实际工程设计中，笔者发现它的分离能力通常超过它的缓冲容积。即分离能力还没有达到最好的情况下，并不够大的缓冲容积就限制了容器选择。要获得更好的分离能力只能选择直径更大的容器。

为了改善这种情况，欧洲的制冷公司设计出了另一种类型的卧式分离容器——容器长度不同。即使容器直径相同，也有两种长度。长度长的一种，制冷量（分离能力）会大许多。比较有代表性的是Star Refrigeration.co.uk，他们的卧式低压循环桶产品^[16]从容器直径ϕ610～ϕ2032mm（表8-8），长度分别是：3m、3.75m、6m以及7.5m。其中直径1220mm的长度有3.75m与6m两种，因此制冷量也有较大的差别。这种产品的另一个特点是容器内部设置挡板和分配槽，目的是可以更好地分离液滴和气体。缓冲容积的计算也与前面的一种不同，因此容器的长度也长很多。这些增加的容积用于贮存蒸发器没有蒸发完回到循环桶的液体。表8-8是这种容器的各种参数，图8-23～图8-25是这种卧式低压循环桶运行不同制冷剂的制冷量。

表8-8 Star Refrigeration.co.uk卧式低压循环桶的参数

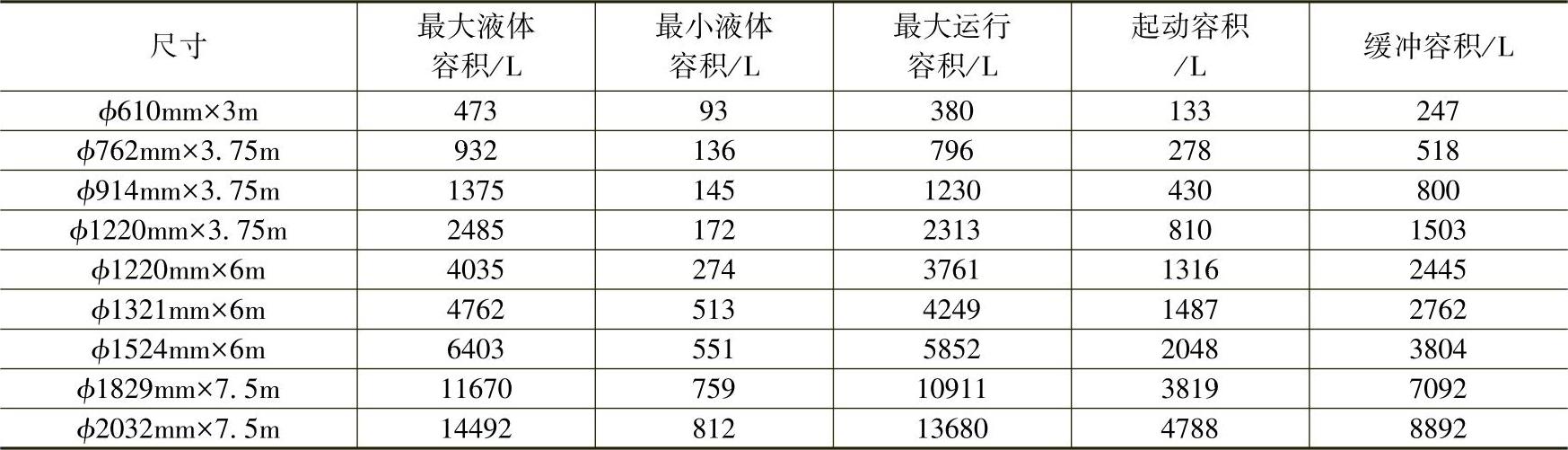
注：起动容积（实际上是稳定容积，各个厂家表达的方式不一样）为75%的蒸发器盘管容积；最大运行容积为运行容积（OPL）；最大液体容积为容器容积×55%；最小液体容积为低液位报警容积。

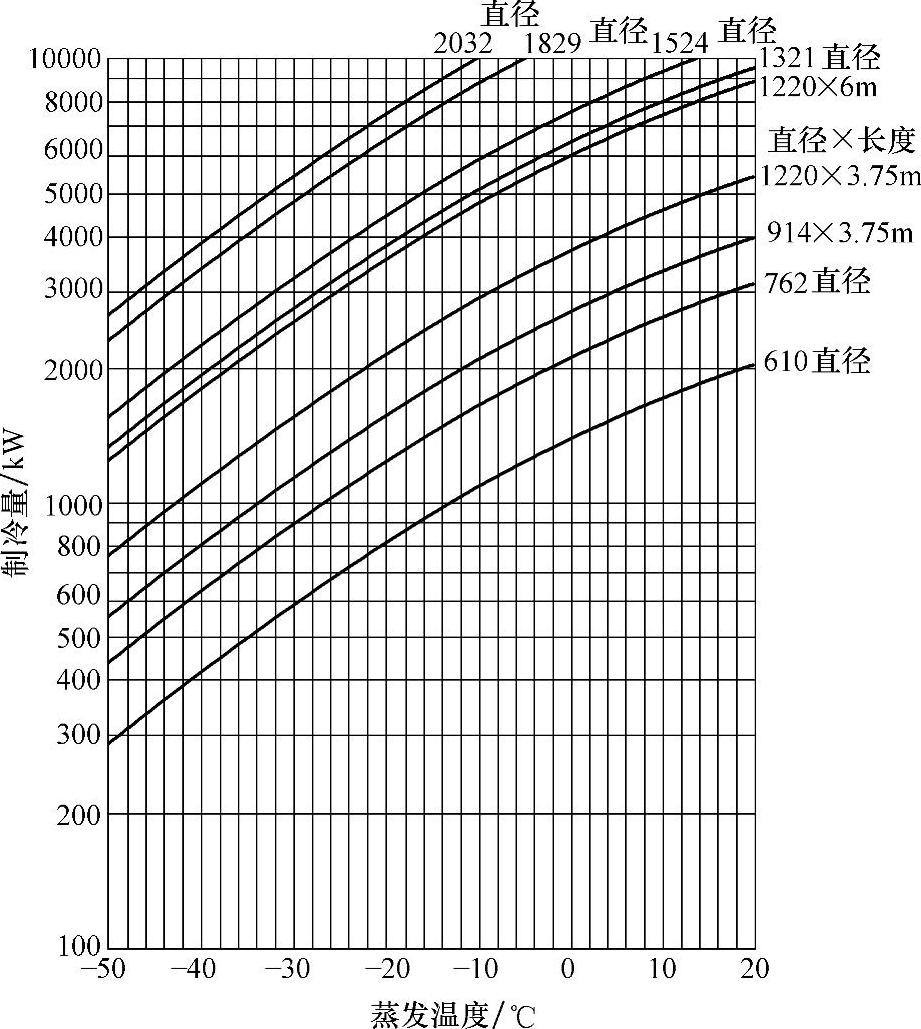
图8-23 R717 Star低压循环桶选型参数

从经济器或者冷凝器供液温度45℃，供液温度35℃增加5%制冷量，供液温度15℃增加14%制冷量，供液温度-10℃增加24%制冷量

由于这家是以工程设计安装为主的公司，因此他们根据容器直径增大的需要，逐渐把容器的有效长度加长。目的也就是增大容器的缓冲容积，使容器的制冷量与缓冲容积的配套差距缩小。

对于第一种低压循环桶的设计，适合于采用冷风机的冷藏冷冻蒸发器，缓冲容积要求不大的场合；对于一些蒸发器需要缓冲容积比较大（如排管）或者循环倍数大的情况（如速冻）、单位容积制冷量比较小的氟利昂制冷系统，采用第二种设计更加合适。这种容器对于

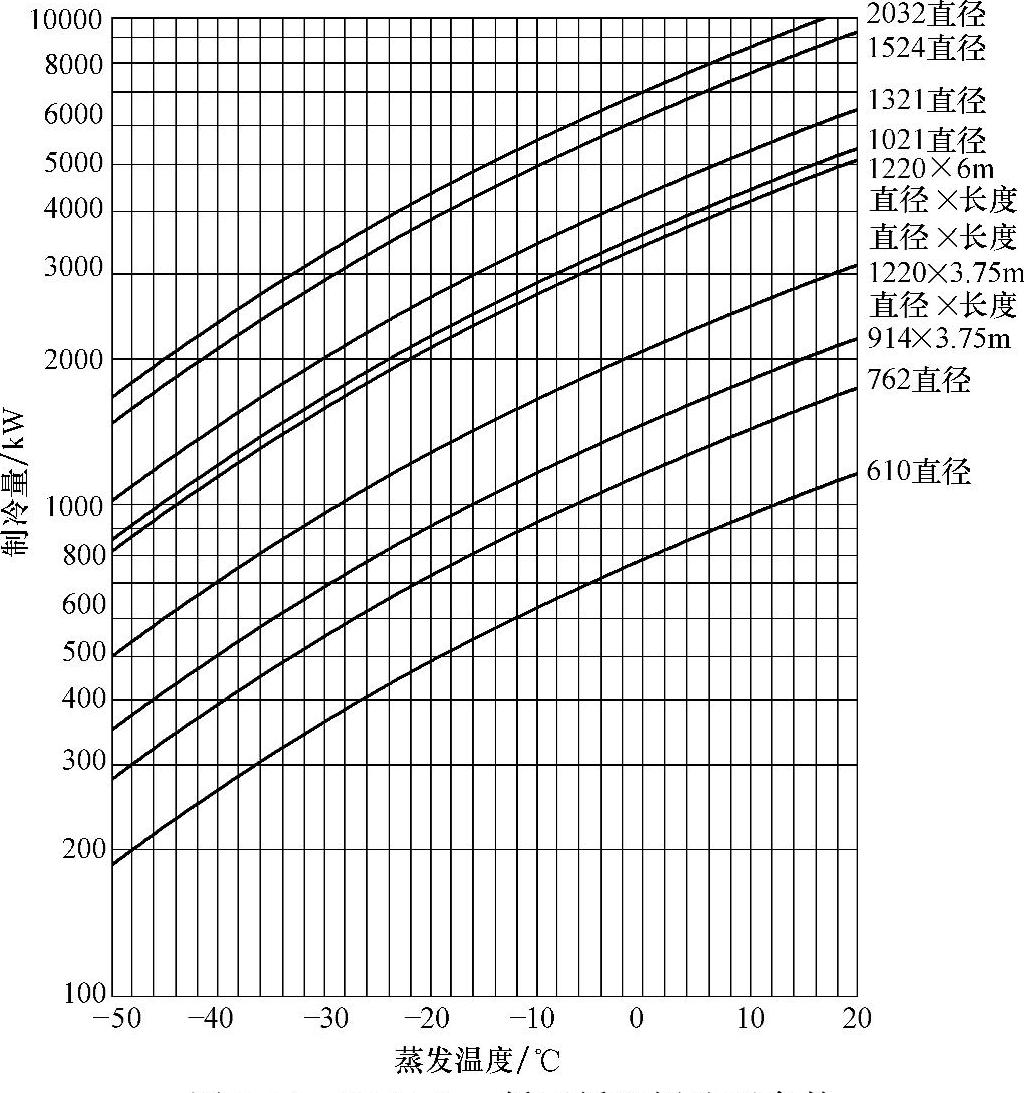
图8-24 R404 Star低压循环桶选型参数

从经济器或者冷凝器供液温度45℃，供液温度35℃增加16%制冷量，供液温度15℃增加44%制冷量，供液温度-10℃，增加77%制冷量

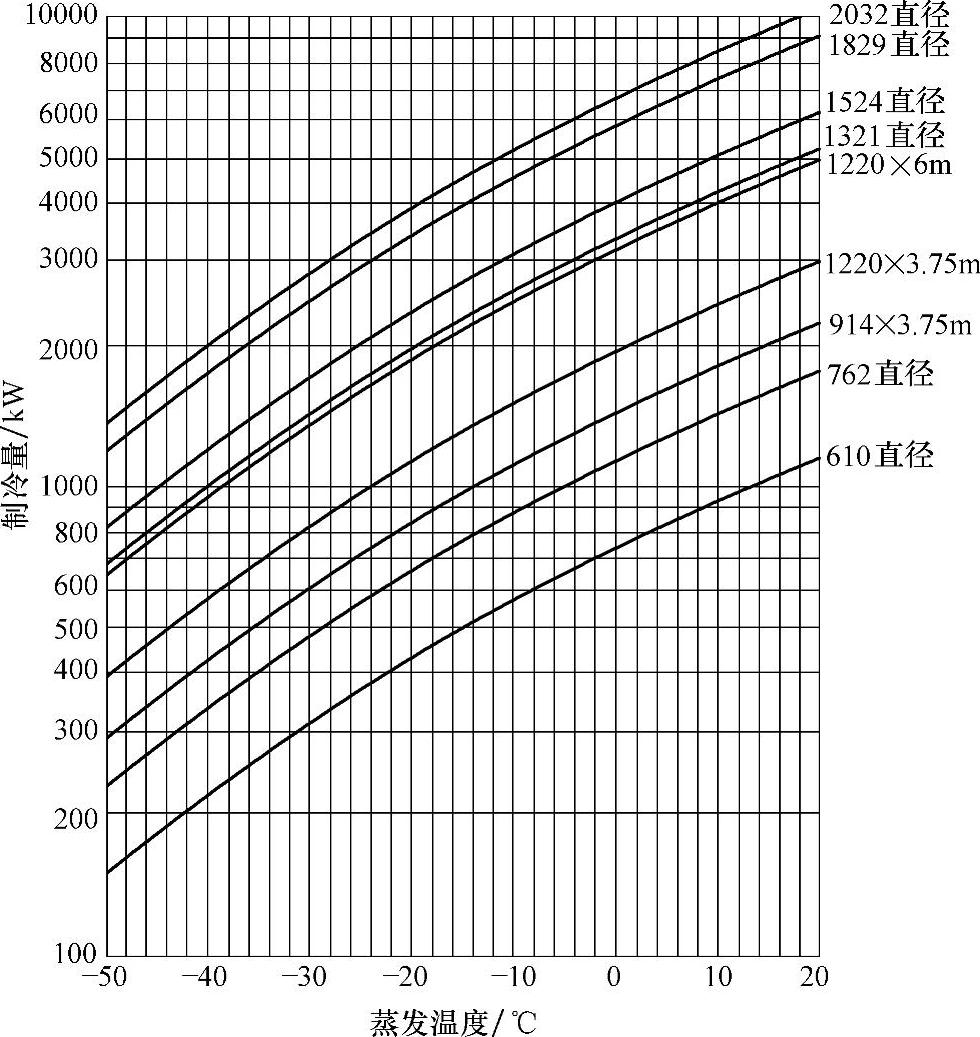
图8-25 R134a Star低压循环桶选型参数

从经济器或者冷凝器供液温度45℃，供液温度35℃增加10%制冷量，供液温度15℃增加30%制冷量，供液温度-10℃增加53%制冷量

一桶多泵的布置形式也容易解决。缺点是容器太长，运输不是很方便。

另一种计算模式是，把阻力系数固定在一个比较高的平均值上。例如氨制冷剂，蒸发温度从20～-40℃，阻力系数从12.528～40.625。生产厂家在计算时，就选择接近30（液滴直径为0.003m）作为固定的阻力系数。根据笔者的推算，参考文献[2]与[3]的立式分离容器计算采用的就是这种固定值，这是笔者对他们的产品计算结果跟踪多年的数据判断。而氟利昂也是基本采用另外一个接近19的固定值（液滴直径为0.002m），这是由氟利昂的特性所确定的。

卧式分离容器的计算需要产品详细的内部结构。除了氨选择接近29的阻力系数以外，其他制冷剂基本上是采用平均最大值（图8-14）再乘以2，这与分离液滴的直径有关。而且随着雷诺数的增大，阻力系数反而减小，这种计算采用的是计算阻力在最不利的情况下的数值。计算的结果中分离速度相对比较小，运行起来更加安全。这些阻力系数的选择也许包括他们在实验中得出的实验值。笔者在书中的举例采用整数值，主要是考虑技术上的问题（与国外在这方面的计算思路相似，在实际应用中采用是没有问题的），仅供参考。