卧式分离容器的分离原理的介绍

卧式分离容器的分离原理计算与立式容器有相当大的区别。在立式分离容器中，主要有三种作用力：重力、浮力和阻力，这些力的方向是相反的（液滴在重力作用下向下，而浮力和阻力向上）。在确立了制冷剂的计算液滴临界直径，以及分离状态下雷诺数的阻力系数后，计算过程相对比较简单。而卧式分离容器制冷剂液滴的运行，除了前面提及的因素外，还增加了将气体中的液滴分离出来的一个水平拖曳力（可以理解为压缩机从分离容器中吸走制冷剂蒸发气体的一个过程）（图8-11和图8-12）^[3]。也就是说需要分离的液滴在分离过程中，除了在自身的重力作用下下降以外，还要受到一个横向牵引力的作用，形成了一个斜向下的合力。为了解决这个问题，引入了一个液滴在卧式容器重力分离中的停留时间τ_R。

根据参考文献[4]的计算，液滴在卧式容器重力分离中，停留时间起重要的作用。停留时间τ_R可用式（8-38）计算：

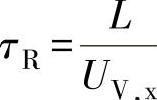(8-38)

式中 L——容器进气口与出气口在x轴方向（水平方向）的长度；

U_V，x——在x轴方向的气体速度。

图8-11 卧式容器中的气体从液体中分离

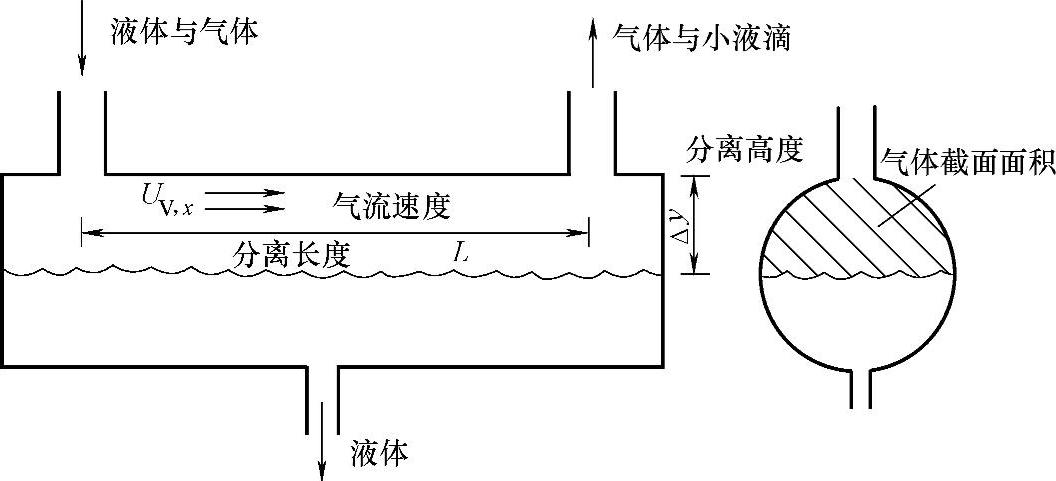
图8-12 卧式容器中的水平速度和分离长度，产生水平停留时间的概念

在停留时间，液滴以终端速度下落。为了使液滴分离发生，液滴必须在规定停留时间内从气体进入的位置落到容器的液面上。用牛顿定律[式（8-9）]解析一系列液滴轨迹：当液滴在y方向（垂直方向）的初始速度为零，气体速度U_V，x在x轴方向的速度，显示制冷剂的液滴加速度到达终端速度是：

1）液滴的下落时间比设定的停留时间还要短。

2）液滴运行对垂直距离只有很小的影响（＜5%）。

因此式（8-9）适用于确定液滴的轨迹，液滴的水平和垂直分离还存在几个关键的差异：

1）没有显著的向上气体的速度抵消重力，其结果需要一个更大的净力来分离液滴。

2）液滴水平分离的问题比较复杂，即在分析上可以分成液滴的有水平运动和垂直运动的液滴轨迹。

因此在停留时间τ_R内液滴的下落距离Δy可以简化为

Δy=τ_RU_T （8-39）

式中 τ_R——停留时间；

Δy——下落距离；

U_T——气体在y轴方向从下落开始净力要求为零的气体速度。

容器的几何形状和液体的高度将决定液滴是否被分离。参考文献[12]根据气流速度与容器截面面积之比，与液体高度与容器直径之比的对应关系，用氨制冷剂实验数据作出图8-13。最大液滴和平均最大液滴下落距离与容器直径的比值为液体高度与容器直径之比的函数，如图8-13所示。(www.xing528.com)

图8-13中v_v是气体在容器液面流过的速度，A_vessel是容器总的截面面积，f₁是气体速度与总的截面面积之比。液体在容器的分离高度增加，气体流过的截面面积减小，如图8-13所示。截面面积减小意味着气体的速度会增加，如果容量（即体积流量）和温度保持不变，截面面积减小意味着气体的速度会增加。增加气体的速度，减少液滴的停留时间，从而使液滴在停留期间的距离减小。

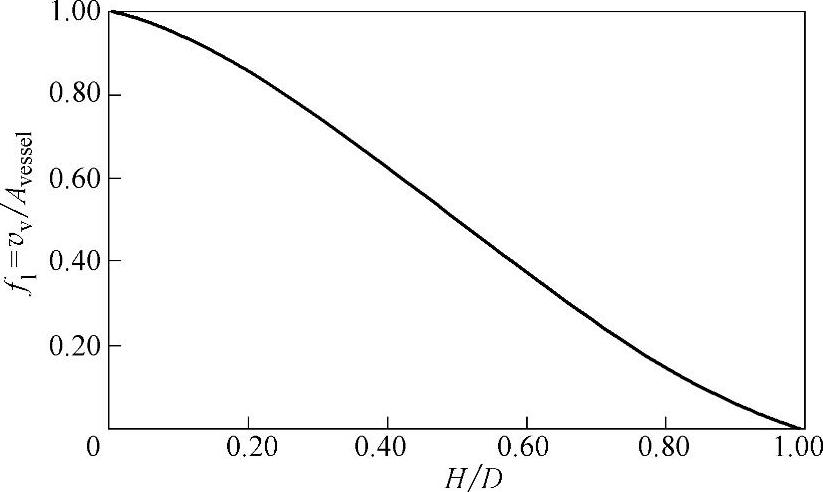
图8-13 气流速度与容器截面面积之比和液体高度与容器直径之比的对应关系

H—卧式容器中液滴下落的距离 D—卧式容器的直径

在图8-14中，f₂是下落距离与分离容器直径之比。液体的分离高度增加结果是所需液滴的分离距离减小。显示最大的下落距离与分离容器直径之比Δy_max/d，与平均下落距离与分离容器直径之比是液体下落高度与容器直径的比值的函数。最大下落距离简单地表示为容器的直径减去液体在容器内的高度。最大的平均下落距离是容器的平均分离高度要大于容器液面的高度。

将式（8-20）和代入式（8-21）得：

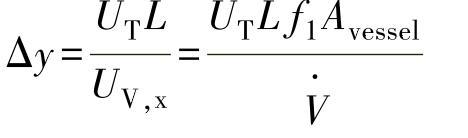（8-40）

式中 f₁——从图8-13查出；

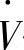——气体流量。

将图8-14中的Δy=f₂D代入式（8-22），并重新整理得：

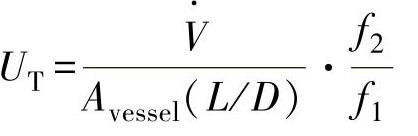（8-41）

式中 D——分离容器的直径（ft）。

图8-14中绘制了f₁和f₂的比例。注意，基本上比例在0.5时，f₁和f₂的比值是恒定的。1.0是最大值，0.78是最大平均值。在H/D的值接近0.5时，意味着在相同尺寸的分离容器内，所有小于容器一半的液面，气体流过液滴的终端速度相同[见式（8-41）]。当容器内的液面高于一半时，液滴的末端速度会增大，分离液滴的尺寸也随之增大。这就是为什么在计算卧式分离容器时以一半液面为计算的基础。

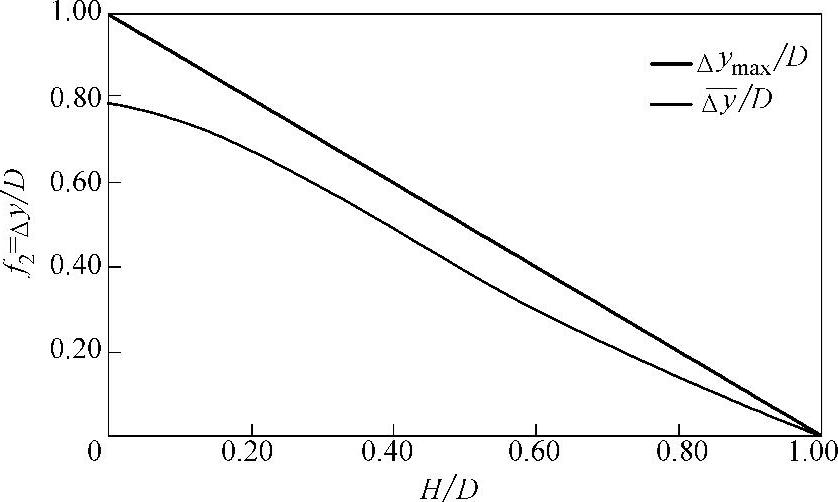
图8-14 最大和平均最大液滴下落距离与容器直径之比在卧式容器长度与容器直径比值上的变化

参考文献[3]认为卧式容器的一半体积是稳定容积和缓冲容积之和。参考文献[13]对卧式容器的建议是：

1）气体空间的最小气体分离高度为15in（0.38m）。

2）不考虑两端封头空间体积。

3）进气口与出气口靠近容器的顶部。

参考文献[3]认为卧式分离容器从气体分离出液体的分离机制与立式分离容器有些不同，但一些原则是相通的。在图8-9的卧式容器中，携带液滴的气体由于重力的原因在横向流动的同时还在下降。液滴进入容器可以认为没有水平或垂直下降的初速度，在重力的作用下垂直加速下降。如果液滴未被带走而下降到液体表面，会溶入液体中。