摄像机成像模型及参数优化

线性模型、非线性模型是摄像机的2种成像模型。小孔成像模型其实就是线性模型的建立准则，小孔成像模型的路径就是摄像机的光轴，透过摄像机光轴中心点将目标物体映射到成像平面上。

为了描述目标物体上的点与其像点的关系，我们通常要建立摄像机坐标系。在进行摄像机标定时，通常要建立摄像机坐标系、图像坐标系和世界坐标等3个坐标系。

3种坐标系之间的转换可以通过数学表达式来实现。在转换过程中需要引入的参数就是摄像机的内外参数。

确定目标点与图像点在各个坐标系中的关系是表述摄像机成像过程的关键：

数字图像通常是通过摄像机拍摄到的目标图像经过数模转换得来的。存储方式就是计算机以一个M×N的矩阵将这些数字图像进行存储。如图8-1所示，图像上某点的像素坐标可表示成（u，v），列数用v表示，行数用u表示。有时需将像素坐标转换为距离坐标，因为要恢复图像在三维空间中的信息，所以表示该点位置必须使用实际距离单位。如图8-1所示，图像坐标系为xO1y。

图8-1　图像坐标系

在xO1y坐标系中，摄像机光心与图像平面的交点通常被定义为原点O1，图像中心处就是该点。设在x轴方向上每个像素点的长度用dx表示，y轴方向上每个像素点的长度用dy表示，原点O1的像素坐标为（u0，v0）。目标物体上某点的像素坐标可表示为：

令kx=1/dx，ky=1/dy，称kx、ky分别为沿x、y轴的尺度因子。

为了简化计算通常用齐次坐标与矩阵形式将式（8-5）、式（8-6）表示为：

图8-2所示为摄像机成像模型的几何关系，其中摄像机光心为O点，Xc轴与图像的x轴平行，Yc轴与图像的y轴平行，摄像机的光轴为Zc轴，图像平面与光轴是垂直的。设图像平面与光轴的交点为图像坐标系的原点，摄像机坐标系是由Xc、Yc、Zc轴和O点组成的直角坐标系。摄像机的焦距为OO1。

图8-2　摄像机成像模型的几何关系(www.xing528.com)

世界坐标系可以表示三维空间中物体相对于摄像机坐标系的位置，我们可以把摄像机放在任何位置。它由XW、YW、ZW轴组成。世界坐标系和摄像机坐标系之间的关系可以用公式（8-8）表示，其中平移向量用t表示，R代表旋转矩阵。

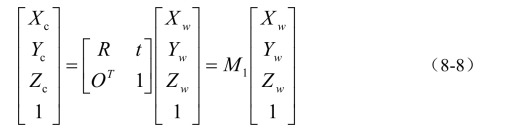
式中：R为3×3正交单位矩阵；t为三维平移向量；O=（0，0，0）T；M1为4×4矩阵。

小孔成像模型可描述空间任意一点P的成像模型，点P在图像上的投影位置是光心O与P点的连线OP与图像平面的交点。这种关系也称为透视投影。由比例关系有如下关系式：

式中：（x、y）为P点的图像坐标；（Xc，Yc，Zc）为在摄像机坐标系中点P的坐标。上述透视投影关系可用齐次坐标与矩阵表示为：

世界坐标系中P点坐标与其投影点的关系可由式（8-11）代入上式（8-8）得到：

式中：f/dx=kx，f/dy=ky；M为3×4矩阵，称为投影矩阵；所以内参数模型可表示为：

由于kx、ky、u0、v0只由摄像机内部结构决定，我们称这些参数为摄像机内部参数。

矩阵

完全由摄像机相对世界坐标系的方位决定，所以称为摄像机外部参数。摄像机标定就是确定某一摄像机的内外参数。