如何计算运动目标的瞬时位姿和速度

在这一部分，我们假设将运动目标的三维空间的Pi映射为由卷帘快门照相机所拍摄的二维空间中的m，我们想利用由三维映射到二维的方法来计算目标在t0时刻的位姿和速度，方程3-12中的比例因子可以由下面的式子得出：

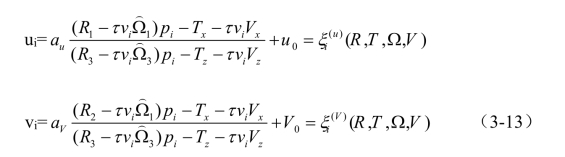
我们应得出（R，T，Ω，V）来化简下列的误差函数：

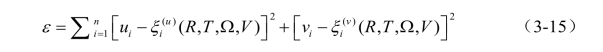
这种带有12个未知数的方程，在得到至少6个有效数的情况下，可以用最佳非线性最小二乘法来解答。这可以被看作是一个带有校准照相机的光束纠正器，注意到，在我们的计算中，旋转矢量R常用q（R）来代替，因此，我们可以令q（R）=1，并将看成是一个已知方程，很明显，这种非线性的算法只能用初设解来趋近于它的准确解。

用卷帘快门相机观察一个移动的多面体，它的直边预计到形象作为曲线轮廓。假设有N个直边，其定义是在对象范围内，他们的方向向量Lk，与一套弯曲的形象轮廓lk匹配。考虑一个在Lk上的任意一点Mk0，任何其他点Mki对后者的优势可以表现在该对象框架如下：

因此，每个像素对曲线可以写成以下投影方程：

这意味着每个像素的等高收益率一对约束的形式：

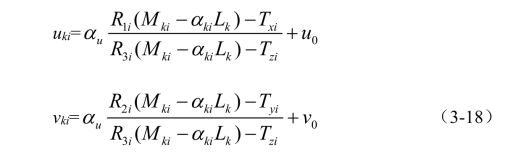
这很明显，相匹配的三维直边与一图像曲线并没有告诉我们每一个轮廓像素相应的三维边缘点。换言之，σki的值是未知之数。因此，方程（3-18）可表示为：

从上式看出，这是一种价值函数应用在最小二乘法的判断用来表示构成和速度参数R，T，Ω，α，V，Σ：

(www.xing528.com)

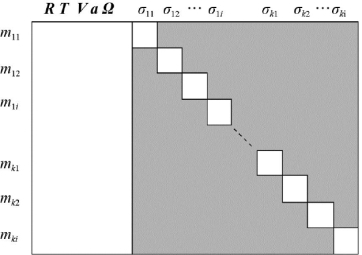
图3-5　雅可比矩J的结构

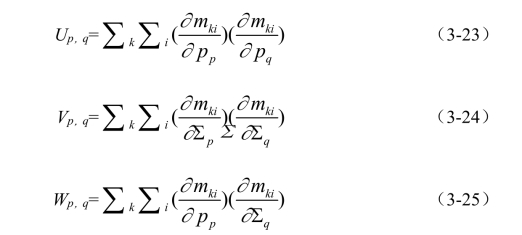
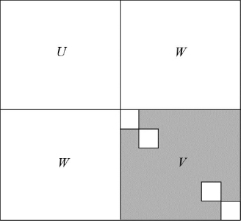
图3-6　JTJ在正规方程式中的结构

一个相似的结构在很多调整器中使用，例如在文献中，为了减少解决正规等式的计算成本，通过把它重写为如下表示：

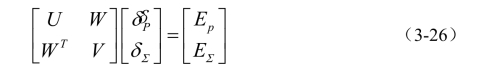
这里δP和δΣ分别包含P和Σ的小变化。EP和EΣ组成正规等式（3-27）右边的向量。

他们的组成定义如下：

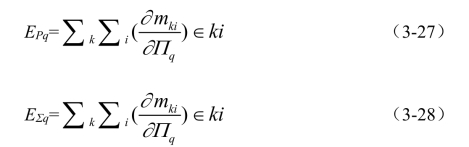
等式（3-26）可以被重写为如下形式：

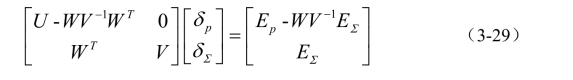
上式可被分解成2个非开的方程式系统如下：

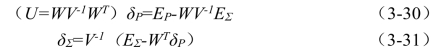
等式（3-30）可以很有效地被解决，因为V是对角线上的元素。等式（3-31）通过式（3-30）的结果解决。