卷帘式快门相机模型优化方法

这部分描述了一个有关卷帘式快门相机的方程式。将展示相机从平行的方向发生向前平行运动所成的投影平面的影响，并且提出一个不依赖于时间的投影方程式。这种方式解释为X缝隙的相机（意味着代替一个针孔投影模型的相机，而这个相机是双缝隙的投影模型）由确定的运动类型扫描。

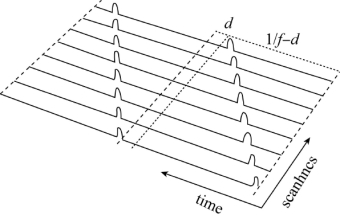
图3-2　曝光过程图

我们以MDCS火线相机的操作为例开始描述，它是一个由Videre设计公司生产的卷帘式快门相机。火线总线有一个运行在8kHz的时钟，因此相机能够以每秒8000个的数据包传送数据。IIDC数字相机说明书上要求在火线上传输的各帧应该等于8000数据包的传输速率。MDCS相机没有足够大的板上缓存来存储一整个帧，因此当从扫描行上读到数据时就尽快发送出去。扫描行继续曝光，读进，立即传送到总线上，这样一帧的总曝光时间就与帧频成反比。帧频（f帧/s），一个扫描行的曝光长度（eμs），扫描行曝光速率（r行/μs），以及帧间延迟（dμs）是可变的，它控制扫描行的曝光。所有的e，r，d通常将依赖于相机的帧频，即f。图3-1为一组扫描行曝光的过程。我们假设曝光时间在扫描行的瞬时时刻，也就是图3-2显示的带有零宽度却结合了一些非零常量的最高点。e的影响是在扫描行中存在非零的运动点，而没有几何影响。

卷帘式快门相机每个像素行按照时间的推移连续扫描而形成一幅图像。我们假设一帧开始于t0时刻，行指针作为一个时间函数表示为：

r是行/μs的速率，v0是第一个曝光扫描行的指针。r取决于传感器是从顶到底扫描还是从低到顶扫描。现在我们假设t0=0。

对于一个理想的透视相机，点的投影以时间为函数使用透视相机方程式决定：

X=（x，y，z，1）属于P3表示空间里相似的静态点；P（t）是以时间为函数的相机矩阵：P（t）=K[R（t）T（t）]和π（x，y，z，1）=（x/z，y/z）。在这里，R（t）是三维定向旋转空间里的元素，T（t）属于R3，因此V（t）=-R（t）T（t）是相机在t时刻视野坐标系统的视点；并且K是一个上三角标度矩阵。图3-3展示了这个结构。

从得到的图象中我们设X为（u，v），它必须满足：(https://www.xing528.com)

对于tc时刻，πy表示为映射π上的y轴部分。方程式（3-7）就是卷帘式快门的常规约束。式子左边表示映射点随着时间推移形成的曲线，式子右边表示以时间为函数的扫描行。扫描行在某时刻如捕获映射点形成的曲线。

如果相机是固定的，也就是P（t）不依赖于t，方程式（3-7）的左边与时间无关，所以图象中的X与tc无关，并且映射结果通常是透视的。然而，通常相机是移动的，并且映射的结果在一些情形中与tc有关。对于一定的P（t）我们能够代入tc来分析，代入tc到等式（3-7）左边获得一个投影式。狭义部分的目的是在一般情况下得到明确的投影。

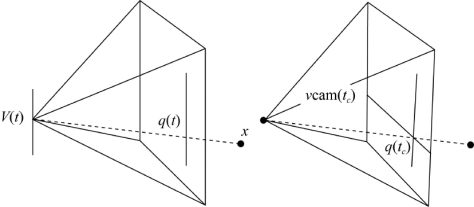
图3-3　投影图

（一）向前平行运动

假设一个标定相机以一定的角速度ω和线速度v运动。一个近似线性的P（tc）给出如下：

当ω=0时，也就是没有角速度的时候，严格线性；否则近似线性。让我们分析匀速向前运动，即v=[vx，vy，0]T，ω=[0，0，ωz）]T代入（3-9）中，即卷帘式快门的约束，在tc产生一个线性等式。假设非一般性的情况，即R（0）=I，T（0）=[0，0，0]T，K=I，在把tc的解代回到q（tc），我们得到：

因此，带有卷帘式快门的相机变成一个在投影几何学上以速度为参数的相机。当固定之后，相机服从针孔映射模型。然而，当相机做匀速线性运动时，相机就可以认为是十字缝隙相机。对于任意点（u，v）我们转化为未知的z，并且证明所有的转化原像都在2条线上：第一条线通过（0，0，0）和（vx，vy，0）；第二条线通过（±1，v0vy/r，vy/r）点，当vx和vy接近零时，这2个缝隙在点（0，0，0）。