在快变输入作用下,传感器的输入-输出关系随时间变化其原因是输入作用引起的系统的暂态分量的影响。因此,系统的动态输出可看成由2个分量构成:一个是像静态特性一样与输入保持确定关系;另一个是由输入作用引起的暂态分量,也称为动态误差。
暂态分量反映了传感器中能量的存储(电场、磁场、位能、动能及热积累等)过程和消耗(摩擦等)过程之间的动态平衡关系。以阶跃函数作为输入,可观察到它们之间的关系。图2-10表示在零初始条件下的阶跃响应曲线,y(∞)表示暂态结束后的稳态值,它与输入x(t)的关系由静态特性确定。由图2-10可见,暂态分量的影响只是在前沿部分显现,故传感器的动态品质参数可用阶跃响应的前沿部分的某些特征来表示,常用如下几种。

图2-10 阶跃响应曲线
1.时间常数τ。传感器输出值由零上升到稳定值的63.2%所需要的时间。
2.上升时间tr。为排除时滞影响,上升时间常定为响应从最初稳态值的5%或10%上升,第一次达到稳态值的90%或95%所需的时间。
3.响应时间ts。指输入量开始起作用到输出值进入稳定值所规定的范围内所需的时间,一般与规定误差一同给出。
4.超调量σp。指输出第一次达到稳定值又超出稳定值而出现的最大偏差,常用相对稳定值的百分比来表示。
5.峰值时间tp。传感器输出值由零上升超过稳定值,到达第一个峰值所需要的时间。
6.稳定时间。指系统从阶跃输入开始到系统稳定在稳态值的给定百分比(规定误差范围)时所需的最短时间。对于稳态值的给定百分比为±5%的二阶传感器系统,ξ=0.707时,稳定时间最短,为3/ω0。稳定时间和上升时间都是反映响应速度的参数。
传感器的动态性能可用一个或几个参数描述。其描述方法与传感器的暂态过程的特点有关。以下是代表暂态过程特点的2种典型过程。
(一)单调变化的阶跃响应(https://www.xing528.com)
由多个惯性环节组成的开环系统,其阶跃响应呈单调变化,可用上升时间、阶跃响应时间或稳定时间三者之一来描述其性能。对简单的、只有一个惯性环节的系统,只须给出时间常数,阶跃响应即可完全确定,如图2-11所示,有:
y(t)=y(∞)[1-exp(-t/τ)](2-22)
可见,τ越小,响应时间和稳定时间越短,动态性能越好。和式(2-17)比较可知,τ变小意味着频带变宽,响应时间变短。
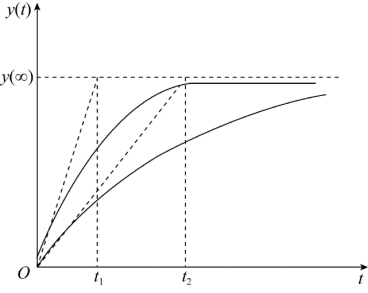
图2-11 一阶系统的阶跃响应
(二)典型的二阶系统
二阶系统的传递函数可由式(2-18)求得,即:

图2-12所示为二阶系统的阶跃响应曲线,图中ξ=0.707的曲线表示临界阻尼状态。比较3条曲线可看出,临界阻尼具有最小的稳定时间,ξ越小则上升时间越短。从响应时间角度看,临界阻尼并非最佳状态。分析表明:ξ越小则瞬时过冲量越大,因此实际中一般(选为0.5~0.7,以便能在允许的冲量下响应时间最比较图2-9和图2-12可看出,较小的ξ值具有较宽的频带(3dB)带宽,故上升时间与带宽有关。

图2-12 二阶系统的阶跃响应
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




