椭圆曲线的测设方法优化为：椭圆曲线测设方法

在建筑工程中，将场区设计为椭圆，在公路桥的桥台锥坡放样中也应用椭圆测设。常用的椭圆测设方法为拉线法、纵横等分图解法和支距法。

1.拉线法

拉线法一般用于在开阔的场区放样整个椭圆线型。如图6-5-8所示，拉线法椭圆测设的步骤如下：

图6-5-8　拉线法椭圆测设

（1）按设计位置确定AB方向及长半轴尺寸ɑ确定A、O、B三点的位置；

（2）确定直线AOB的垂线COD的方向，根据短半轴尺寸b定出C、D两点；

（3）根据焦距确定焦点F1和F2的位置；

（4）取一根没有弹性的细绳，使其长度为2ɑ，两端分别固定在F1和F2上；

（5）用圆棍套住细绳后，在AB两边画曲线；

（6）检核：观察曲线是否通过A、B、C、D四个点。

2.纵横等分图解法

纵横等分图解法测设椭圆时，不需要进行计算，只需等分直线，应用比较灵活。

如图6-5-9所示，图6-5-9（a）和图6-5-9（b）的测设方法相同，四分之一椭圆的测设步骤如下：

（1）定出轴线OA和OD的方向；

（2）测设矩形AODE或平行四边形AODE；

（3）将直线AE和ED进行10等分，并从直线的起点开始进行编号1、2、…、9；

（4）以直线AE上的各点为起点，依次连接直线ED上的各点，连接的直线分别为A—1、1—2、2—3、…、9—D；

（5）直线两两相交的交点分别为Ⅰ、Ⅱ、Ⅲ、…、Ⅷ、Ⅸ；

（6）将A、Ⅰ、Ⅱ、Ⅲ、…、Ⅷ、Ⅸ、D各点用光滑的曲线连接，观察曲线的形状，在点疏的地方可以用相同的方法进行加密。

图6-5-9　纵横等分图解法椭圆测设

（a）矩形图解；（b）平行四边形图解

3.支距法

支距法即独立直角坐标法。如图6-5-10所示，以椭圆的中心为坐标原点，以长半轴为x轴，以短半轴为y轴建立直角坐标系。

测设椭圆曲线，计算的测设数据为椭圆方程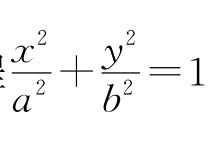，若以y轴为自变量，以x为函数，则按公式计算测设数据。

如图6-5-10所示，支距法测设椭圆的步骤如下：

（1）建立直角坐标系；

（2）测设矩形AOCD；

（3）将短半轴10等分，等分点的编号为1、2、…、9；

（4）计算测设数据，见表6-5-1；

（5）以短半轴为基准，垂直量出x或ɑ－x，定出椭圆上的点；(www.xing528.com)

（6）检核：观察曲线的形状，在点疏的地方用相同的方法进行加密，加密椭圆的测设数据为表中自变量。

【例6-5】　如图6-5-11所示的组合图形为斜桥桥墩的横截面，桥墩纵、横轴线的夹角为70°，要求根据图中所示数据，在平行四边形的两端分别测设半个椭圆。

图6-5-10　支距法椭圆测设

图6-5-11　斜桥桥墩横截面

表6-5-1　支距法椭圆测设数据计算表

【解】　可以用多种方法测设椭圆曲线。

方法一：支距法

支距法测设椭圆的步骤如下：

（1）如图6-5-12（a）所示，建立直角坐标系；

（2）以x为变量，以为函数计算测设数据，见表6-5-2；

表6-5-2　支距法椭圆测设数据计算表

（3）如图6-5-12（b）所示，取直线BC的中点A，测设直线AD，使∠BAD＝70°；

（4）设直线BC为x轴，将其12等分，设直线AD为y轴，根据表6-5-2的数据，在斜轴坐标系中，确定定位点；

（5）将各定位点连接成光滑的曲线，即测设的椭圆曲线。

方法二：拉线法

（1）如图6-5-12（b）所示，测设∠BAD的分角线方向，定出E点；

图6-5-12　椭圆测设例题－支距法、拉线法

（a）支距法；（b）拉线法

（2）测设与分角线AE垂直的方向，定出F点；

（3）计算测设数据：

在△A12中，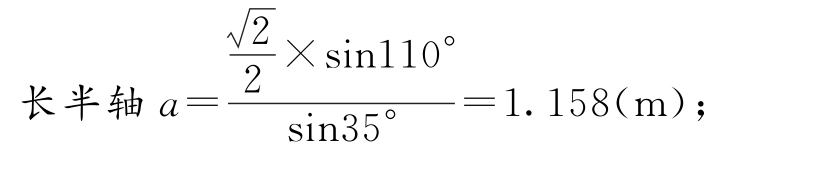

在△A23中，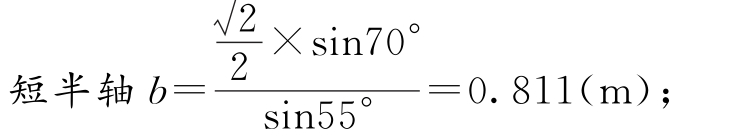

焦距。

.827m，定出F2点；

（5）设置拉线长度为2.316m，两端分别固定在F1和F2上，用圆棍套住细绳，用拉线的方法在地面上画出椭圆曲线。

方法三：纵横等分图解法

（4）沿AE方向量0.827 m，定出F1点，沿EA的延长线方向量0分别将BE、ED、DF、FC四条直线12等分，用纵横等分图解的方法在椭圆曲线上定出若干点。

如图6-5-13所示，将三种方法测设的椭圆曲线进行对比发现：拉线法和支距法测设的椭圆曲线完全相同，而纵横等分图解法测设的椭圆曲线较前两种稍有不同。

图6-5-13　多种方法测设的椭圆图形对比