小三角测量内业工作优化方案

小三角测量内业计算的最终目的是计算各三角点的坐标。内业计算前，应仔细全面地检查测量的外业记录，检查数据是否齐全，有无记错、算错，是否符合精度要求，起算数据是否准确，然后绘制出略图，在图上注明高级控制点（已知点）及三角点点号等。数值计算时，角度值取至秒，长度和坐标值取至毫米。下面分别介绍单三角锁和大地四边形的近似平差计算。

1.单三角锁的计算

如图3-6-2所示，单三角锁应满足两个几何条件：一是图形条件，即各三角形内角和应为180°；二是基线条件，即由起算边D0用内角推算的终边基线长度应等于实测值Dn。计算前，先绘制计算略图，并对三角形的内角进行编号。按推算方向，将传距边（又称前进边）所对的角编号为ɑi，已知边所对的角编号为bi，第三边（又称间隔边）所对的角编号为ci。

（1）角度闭合差的计算与调整——第一次角值改正。由于角度观测值带有误差，以致不能满足图形条件，产生角度闭合差fi，即

图3-6-2　单三角锁

fi容许值随等级而异，对于图根级小三角容许值为±60″。角度闭合差调整的原则：将fi以反符号平均分配到各观测角；若不能均分，将余数分配给大角所对应的改正数上，即各角度的改正数为

则各三角形内角调整以后的值（又称为改正值）为

调整后的内角和必须等于理论值，即

（2）基线闭合差的计算与调整——第二次角值改正。根据正弦定理，用改正后的角值按计算D1、D2、…、Dn的推算程序列基线方程式

由于经第一次改正后的角值及丈量的基线均不可能完全没有误差，而产生基线闭合差。因为基线丈量的精度较高，其误差可略去不计，故仍需要对角进行第二次改正，以消除基线闭合差。欲使，应对加上第二次改正数即

对式（3-6-5）两端取自然对数，即有

由于各改正数的绝对值一般都很小，故式（3-6-6）中各正弦对数可用泰勒级数展开，仅取其前二项得

式中　——一般为秒单位，则ρ″＝206265″。

将式（3-6-7）代入式（3-6-6），即有

将式（3-6-8）整理后得

式中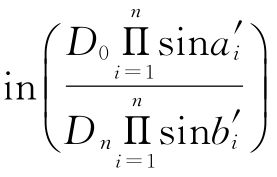，的值趋近于1，且大于1/2，根据幂级数展开式二次以上高次项略去，得

将式（3-6-11）代入式（3-6-9），即得基线条件方程式的最后形式，即

由于测角精度相同，为了不破坏已满足精度要求的图形条件，改正数绝对值相等而符号相反，即

解出第二次角值改正数为

最后的平差角值Ai、Bi、Ci应为(www.xing528.com)

平差角应满足所有条件方程式，以作校核，即

（3）边长和坐标的计算。根据基线长度和平差后的角值用正弦定理可以算出锁中其他各边长度，从图3-6-2第Ⅰ个三角形中，可以写出

这样就可以计算出AC和BC的边长。同理，可以推算出三角形Ⅱ、Ⅲ…各边的长度，直至终边Dn校核正确时为止。各三角点的坐标可按闭合导线进行推算。表3-6-2所示为单三角锁平差计算表。

表3-6-2　单三角锁平差计算表

2.大地四边形的计算

如图3-6-3所示，在大地四边形中，AB边为已知边或基线边。当AB边为基线边时，A、B两点至少有一个点为已知点，且AB边的坐标方位角应为已知。从AB边开始，沿顺时针方向将各个观测内角编号为ɑ1、b1、ɑ2、b2、ɑ3、b3、ɑ4、b4。大地四边形的内业计算与单三角锁的内业计算的基本思路是相同的，但是由于网形的区别，其计算方法也略有差异，下面就介绍大地四边形的近似平差计算。

图3-6-3　大地四边形

（1）角度闭合差的计算与调整——第一次角值改正。大地四边形可列出多个图形条件方程，其中只有三个是独立的。这里取四边形内角和及两个对顶角为图形条件，即

因为角度观测带有误差，使上述条件不能满足，故产生闭合差：

角度闭合差按等精度观测平均分配的原则，为了消除f1，每个角度应该改正－f1/8；为了消除f2并使改正后第一个条件不受破坏，ɑ1、b1应各改正－f2/4，而ɑ3、b3应各改正＋f2/4；同理，ɑ2、b2应改正－f3/4，ɑ4、b4应改正＋f3/4。所以，第一次角值改正数应为

第一次改正后的角值应为

调整后的各角应满足以下条件：

（2）基线闭合差的计算与调整——第二次角值改正。与单三角锁基线条件式相似，根据正弦定理，用第一次改正后的ɑ′i、b′i，从起始边AB出发，依次进行推算，得边长条件方程式：

计算第二次改正数的方法也完全相似，其改正数为

式中

最后平差角值Ai、Bi应为

平差角应满足所有条件方程式，以作校核，即

（3）边长和坐标计算。根据平差后的角值和起始边长推算各边长，校核无误后可按闭合导线推算各三角点坐标。表3-6-3所示为大地四边形平差计算表。

表3-6-3　大地四边形平差计算表