支持向量分类机的工作原理简介

支持向量分类机的本质就是对样本数据求分类函数，也就是模型的决策函数，根据决策值正确划分样本类别，如下式：

其中，wTx+b=0表示分类的超平面，记为L。w是法向量，为垂直于超平面的方向。b是样本到超平面之间的距离。对于点（xi，yi），当wTx+b＞0时，该点为一类；当wTx+b＜0时，该点表示另一类。如图9-3-1所示，白色圆圈为一类，黑色圆圈为一类，超平面L就是模型的决策函数。假设，f（x）＞0的点类别为1，f（x）＜0的点类别为-1。

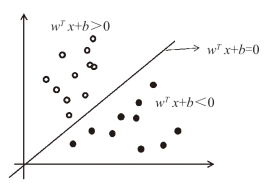
图9-3-1　二分类示意图

（一）支持向量分类机的最优平面

求解支持向量分类机的最优分类函数就是寻找支持向量的最优平面。如下图9-3-2所示，白色类距离超平面最近的直线是L1，黑色类距离超平面最近的直线是L2。L1和L2之间的距离称为分类间隔。分类间隔为两类样本中离超平面最近的两点间的距离。

对于样本来说，分类超平面有很多，但是只有使分类间隔最大时的分类超平面为最优分类平面。此时，在支持向量机中寻找决策函数问题，就变为寻找超平面间的最大分类间隔问题。我们假设所有数据点离最优分类平面的距离都大于1，就可以实现正确分类，那么样本（xi，yi）满足下式：

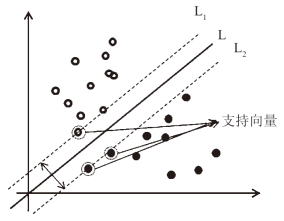
图9-3-2　支持向量机线性分类示意图

故样本到分类超平面的距离的绝对值为：

根据图9-3-2所示，距离超平面L最近的几个样本数据使得上式的等号成立，点到分类平面的距离为1，我们称这几个点为支持向量。支持向量之间的间隔为：

对于最好的分类平面来说，γ值最大，那么寻找最优分类平面就变为寻找w和b使得最大的问题，数学表达式如下式所示：

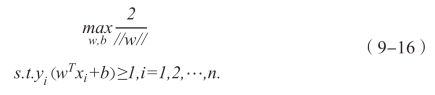
显然为了最大化间隔，仅需要最大化|| w ||-1，这就等价于最小化|| w ||2，那么上式就变为：

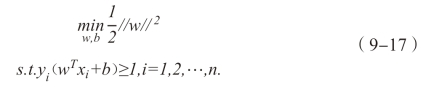(www.xing528.com)

对此，构建拉格朗日函数

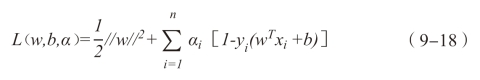
其中，αi为拉格朗日系数。

对w、b、αi求偏导等于0得：

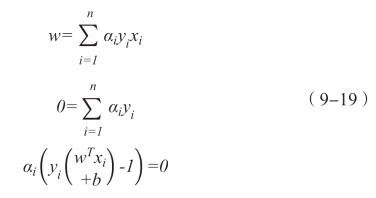
将上式代入拉格朗日函数，原来的问题就转化为凸二次规划对偶问题，如下式：

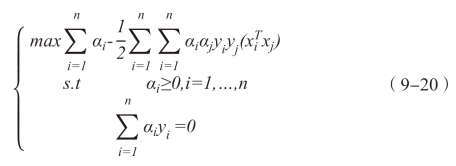
可以看出，式（9-20）就是在不等式约束下求解二次函数的极值问题，这表明会存在唯一优解。将最优解w*、b*代入式（9-12）就可以得到分类的最优平面，如下式：

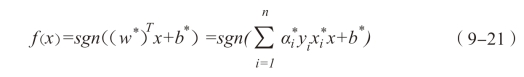
当样本数据量较大时，会有一些噪声数据影响分类结果。为了最大化间隔的同时，不满足约束的样本要尽可能少，也就是被错误划分种类的样本要少，所以，在此基础上增加松弛因子ξ和惩罚参数C，那么优化目标就变为：

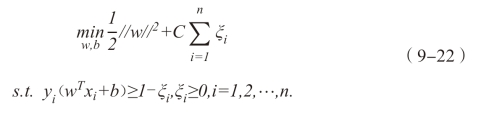
其中松弛因子ξ是用来衡量预测结果与样本实际结果的便利程度，它的值越小，说明模型的鲁棒性越好。惩罚参数C是用来代表错误划分样本的惩罚力度，用于调节正则化和经验风险之间的平衡。

（二）核函数

对于在样本空间内无法线性可分的情况，我们可以将样本空间映射到高维空间来实现线性可分。在支持向量机中采用核方法，也就是引入核函数的方法将输入变量映射到高维空间。根据大量研究，常用的核函数有以下5种：

表9-3-1　常用的核函数

对于核函数的选择通常没有绝对的标准，它在不同的模型中性能表现各不相同。多项式核函数的计算量比较大，尤其当特征空间位数很高的时候，会出现无法得到正确结果的情况，但是径向基函数（RBF）不存在这样的情况。同时，Sigmoid核函数和径向基核函数（RBF）拥有相似的功能，一般情况下会优先考虑使用径向基核函数（RBF）。所以本文将选取RBF作为核函数。引入核函数后，优化目标就变为：

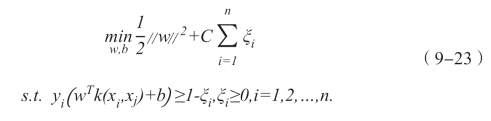
求解式（9-23）的最优解就可以得到要找的最优分类平面，计算方法和上述过程一致，以此划分样本类别。