【摘要】:Barabási和Albert最先指出“度值分布是否符合幂律分布”是判断网络是否具有“无标度”属性的关键,无标度网络中节点的度值与节点度值排序在双对数坐标下呈“双截尾幂律分布”,关于双截尾幂律分布的数学解析和物理意义参考Reed的相关文献,本文不再赘述。从度分布函数式(7-2)、式(7-3)、式(7-4)可知,贸易网络和航空网络、海运网络都具有无标度网络的特性,在三个网络中节点都具有较显著的差异性,都存在少数发挥着关键作用的核心节点。
节点的度分布P(k)指的是网络中任意一个节点度值为k的概率。Barabási和Albert最先指出“度值分布是否符合幂律分布”是判断网络是否具有“无标度”属性的关键,无标度网络中节点的度值与节点度值排序在双对数坐标下呈“双截尾幂律分布”,关于双截尾幂律分布的数学解析和物理意义参考Reed的相关文献,本文不再赘述。将前文测算出贸易网络、航空网络、海运网络度值进行度分布分析,在双对数坐标系下得到三者的分布,如图7-2-1、图7-2-2、图7-2-3所示。

图7-2-1 贸易网络中的度分布图

图7-2-2 航空网络中的度分布图(https://www.xing528.com)
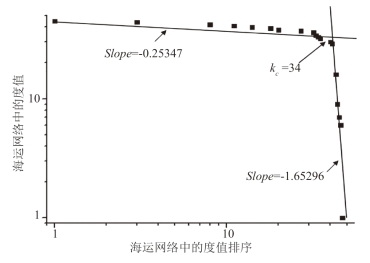
图7-2-3 海运网络中的度分布图
从图7-2-1、图7-2-2、图7-2-3可见,三个网络都服从“双截尾幂律分布”,对其节点分布进行曲线拟合,贸易网络和航空网络、海运网络度分布函数分别为式(7-2)、式(7-3)、式(7-4)所示。

从度分布函数式(7-2)、式(7-3)、式(7-4)可知,贸易网络和航空网络、海运网络都具有无标度网络的特性,在三个网络中节点都具有较显著的差异性,都存在少数发挥着关键作用的核心节点。相比于贸易网络和海运网络,航空网络的节点在网络中的地位和作用差异性更大。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




