不同城市丝路经济带联结程度比较

前面分析了所选取“丝路经济带”沿带各城市的对外经济联系总量，那么经济联系强度在时空上有何差异则通过全局和局部自相关性进行分析说明。

（一）空间权重矩阵的确定

为了更好地反映研究区内各城市间的空间关联度和经济联系强度，采取加权平均旅行时间距离的导数作为空间权重。因为相比于确定空间权重矩阵的两种常用算法：基于多边形公共边和基于多边形质心直线距离来说，使用加权平均旅行时间距离的导数来衡量空间权重更为精确有效。

（二）全局空间自相关测度

在式（6-6）的基础上，得到全局空间自相关测度如式（6-10）所示。

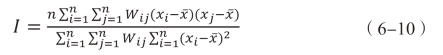
其中：xi、xj为城市i、j的经济联系强度；Wij为建立的空间权重矩阵；n为研究区内的121座城市。

利用Open Geo Da软件计算得到的“丝路经济带”各城市经济联系强度综合得分的全局自相关Moran指数I的值为 0.4562，小于1，虽然属于正相关范围，但相关性较低。这说明就“丝路经济带”，从整体来看，各节点城市的对外经济联系强度在空间上具有聚类特征，但聚类特征不明显。即经济联系强度大的城市与经济联系强度大的城市相邻接，对外经济联系强度低的城市与对外经济联系强度低的城市相邻接。(www.xing528.com)

（三）局部空间自相关测度

为了能进一步更直观地揭示“丝路经济带”不同经济发展水平的城市对其他城市经济联系强度在局部范围内的相关关系，则采用空间自相关的局部指标之一 Local Moran’s I 来测量节点城市i与相邻接的节点城市j之间经济联系强度的相关性。

利用式（6-8），经计算，结合Arc GIS和Open Geo Da软件得到Moran散

点图，如图6-3-1所示。

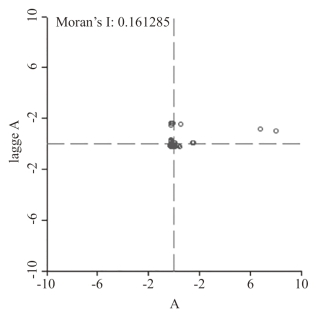
图6-3-1　Moran散点图

由图6-3-1可知，基于铁路网的经济联系的Moran’s I指数点大部分落在第I和第II象限内且集中在0附近，呈现高高和低高集聚，说明就经济联系强度这一属性存在空间集聚。

所选的121座节点城市间集聚性较差，其中59座城市之间经济联系强度无显著性，这些城市主要集中在亚洲国家，表明集聚现象不明显；“低—低”类型的城市共有52座，主要分布在东欧国家，表明这些城市与邻近城市经济联系不紧密，没能在发展自身经济的同时带动邻域其他城市的经济发展；“高—高”类型存在于位于巴基斯坦的拉合尔市与位于印度的阿姆利则市，表明这两座城市经济发展迅速，城市自身均衡性较高，对另外一座城市的经济关联带动作用也较强；“低—高”类型的城市集中在印度、孟加拉国和巴基斯坦，表明这些城市自身对外经济联系较弱，而邻域城市对外经济联系较高；不存在“高—低”类型的城市，表明研究区中不存在某一城市对外经济联系强度较高，而其邻域城市对外经济联系强度弱的现象。