实证分析：海上丝绸之路远洋航运网络的牵制与控制

从远洋航运网络可靠性分析的角度上看，节点机场包括“正常”与“瘫痪”两种状态。以各航班在机场内平均等待服务时间为标准，运用排队论原理，可以得出中国远洋航运网络节点的线性耦合常微分方程为式（5-8）。

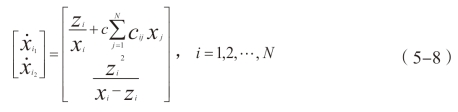
其中：表示节点港口的瘫痪状态；表示节点港口的正常状态；N＞1：远洋航运网络中节点港口数目；Zi表示第i个节点港口的正常情况单位时间内的平均吞吐量；xi：表示第i个节点港口受到外界干扰时单位时间内的航班服务数；c＞0是远洋航运网络的耦合强度，表示各节点城市之间的相互影响关系，可以用远洋航运网络中节点城市“度”的平均值来表示，中国远洋航运网络各节点度的平均值为c=55.41；C=（cij）N×N：耦合矩阵，反映远洋航运网络的拓扑结构，即已采集到的124×124的远洋航运网络邻接矩阵A。

将实现节点机场的正常功能为控制均衡点，按式（5-6）建立远洋航运网络节点的牵制网络方程，并利用赵军产等学者提出的算法：先确定网络的最小耦合强度与最少牵制节点后，然后不断增加牵制节点，最终选择一个合适的α，使代价函数Q（r，d）达到它的最小值，进而得到最优的（r，d）组合，计算出远洋航运网络的受控点数量与反馈增益系数的可行组合情况（r，d）如表5-4-1所示。

表5-4-1　部分可行组合表(www.xing528.com)

当α在［0.1］之间取不同值时，对于上述可行组合Q（r，d）=rα d1-α值得变化情况如图5-4-1所示。

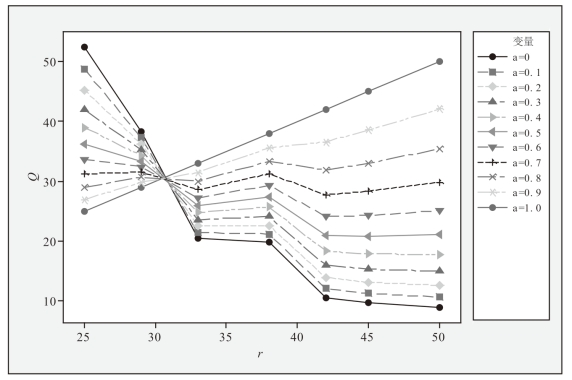
图5-4-1　α=0，0.1，0.2，…，1时可行组合对应的Q值

通过计算可知，当α=0.5时同时兼顾了r，d的取值，此时当r=25时，Q有最小值min（Qα = 0.5，R = 45）=20.784 61。即对于中国远洋航运网络，只要有选择地控制25个关键节点，就能够以储备受控节点9.6%的服务能力为代价，实现对整个网络的有效控制。