定向持续干扰模式对海上丝绸之路航运可靠性的影响研究

（一）“定向持续干扰”模式的仿真系统设计的思路

“定向持续干扰”模式是指根据既定的方案对远洋航运网络中的节点进行依次干扰的模式。在定向干扰型仿真系统中，将会有选择地破坏某些重要节点。在远洋航运网络中，度、介数和聚类系数是反映通航城市重要性的三个关键指标，因此需要借助这三者以作为定向干扰的依据。分别计算出各通航港口的度、介数和聚类系数，并按由大到小排序，然后分别参照度排名、介数排名、聚类系数排名以及三者排名次序之和这四个标准作为反映通航港口重要性的判定指标，按照从大到小的次序排序，分别进行四次攻击，根据计算结果以确定最终的定向干扰方式。

定向干扰型仿真系统设计的主要思路：定向干扰型仿真系统参照一定标准，有目的性地对重要通航港口进行破坏。在远洋航运网络邻接矩阵A中，按既定次序，依次选取节点，并在远洋航运网络邻接矩阵中删除该通航城市以及与其通航城市的所有航班，形成新的远洋航运网络邻接矩阵A3；重复上述步骤，直至受干扰的通航港口数量达到要求，具体思路如图5-3-5所示。

（二）“定向持续干扰”模式对远洋航运网络可靠性影响的仿真分析

1.“度”值标准下的仿真分析

在按照度排序的定向干扰仿真系统中，以干扰城市依次递增的方式进行124次干扰仿真，即第一次仿真，按两种不同的干扰策略均只影响远洋航运网络中的一个通航港口，得到新的远洋航运网络邻接矩阵Y1，第二次仿真则将受干扰城市增加到两个，得到远洋航运网络邻接矩阵Y2，依此类推，共计进行124次仿真，得到124组Y矩阵。分别计算f、l、s 三个参数值。如图5-3-6。

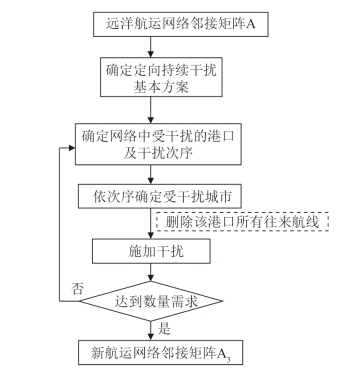
图5-3-5　定向干扰型仿真系统设计思路

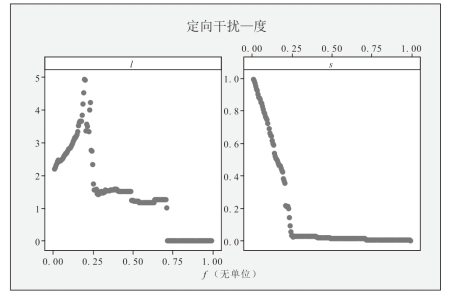
图5-3-6　“度”值标准下f和l、f和s变化关系图

（1）在定向干扰型—按照度标准的仿真系统中，l值先急剧增加，后快速降为0，变化幅度大，说明按照度标准下的定向干扰对远洋航运网络的功能可靠性影响显著；随着越来越多的节点被干扰，节点之间的连通性逐渐下降，在被干扰的节点达到一定的数量之后，远洋航运网络中的节点相互孤立，网络中随即不存在任何连接，此时l值下降为0，f=0.68；f ＞0.68后，整个网络便处于瘫痪状态。

（2）在定向干扰系统中，s值下降快速，当f=0.25时，s值趋于0，表明远洋航运网络非常容易在“度”值标准下定向持续干扰仿真中陷入瘫痪，即“度”值标准下定向持续干扰对中国远洋航运网络的效率可靠性影响较大。

2.“介数”标准下的仿真分析

在按照介数排序的定向干扰仿真系统中，以干扰港口依次递增的方式进行124次干扰仿真，即第一次仿真，按两种不同的干扰策略均只影响远洋航运网络中的一个通航港口，得到新的远洋航运网络邻接矩阵Y1，第二次仿真则将受干扰港口库增加到两个，得到远洋航运网络邻接矩阵Y2，依此类推，共计进行124次仿真，得到124组Y矩阵。分别计算f、l、s 三个参数值。如图5-3-7。

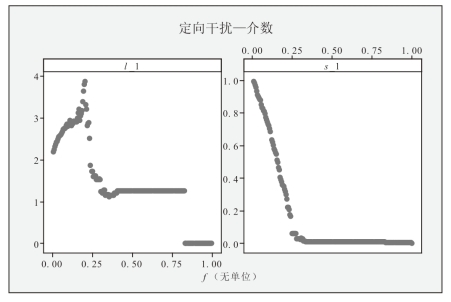
图5-3-7　定向干扰∶按照介数标准下f和l、f和s变化关系图

（1）“介数”标准下，l值先增加，后降为0，变化幅度大，说明按照介数标准的定向干扰对远洋航运网络的功能可靠性影响明显；被干扰节点数增加，节点间连通性持续下降，当f=0.76时，l值下降为0，网络中随即不存在任何连接；f ＞0.76后，整个网络便处于瘫痪状态。

（2）“介数”标准下，s值快速下降，当f=0.25时，s值趋于0，表明远洋航运网络非常容易陷入瘫痪，即“介数”标准下定向干扰对中国远洋航运网络的效率可靠性影响较大。

3.“聚类系数”标准下的仿真分析

在按照聚类系数排序进行124次干扰仿真，即第一次仿真，按两种不同的干扰策略均只影响远洋航运网络中的一个通航港口，得到新的远洋航运网络邻接矩阵Y1，第二次仿真则将受干扰港口增加到两个，得到远洋航运网络邻接矩阵Y2，依此类推，共计进行124次仿真，得到124组Y矩阵。分别计算f、l、s 三个参数值。如图5-3-8所示。(www.xing528.com)

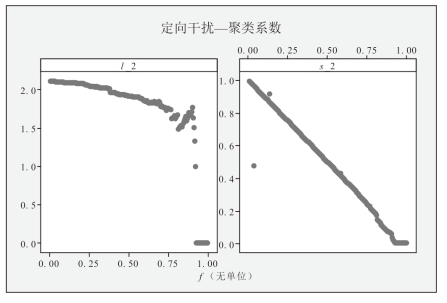
图5-3-8　“聚类系数”标准下f和l、f和s变化关系图

（1）“聚类系数”标准下，l先减小，然后增加，最后降为0。随着被干扰节点的数量逐渐增多，l值减小，说明在此区域内存在降低网络便利性的节点，在该节点删除后，整个网络的平均最短路径变小。而随后l值急剧降为0，说明接下来被干扰的这些节点对中国远洋航运网络的功能可靠性起着至关重要的作用。

（2）“聚类系数”标准下，s值下降快速，但减速相对较慢，当f=0.8时，s值趋于0，说明在这种标准下80%的节点被删除后，远洋航运网络才会出现瘫痪的情况，与前两类标准下定向干扰结果相比，按照聚类系数对网络进行定向干扰时，中国远洋航运网络的效率可靠性受影响程度较小。

4.“多参数”标准下的仿真分析

“多参数”标准下，按照度、介数和聚类系数排名之和确定受干扰港口，并进行124次干扰仿真，即第一次仿真，按两种不同的干扰策略均只影响远洋航运网络中的一个通航港口，得到新的远洋航运网络邻接矩阵Y1，第二次仿真则将受干扰港口增加到两个，得到远洋航运网络邻接矩阵Y2，依此类推，共计进行204次仿真，得到204组Y矩阵。分别计算f、l、s 三个参数值。如图5-3-9所示。

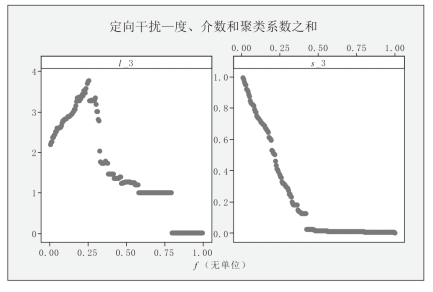
图5-3-9　“多参数”标准下f和l、f和s变化关系图

（1）“多参数”标准下，l值先增加，后降为0，变化幅度大，说明按照综合标准下的定向干扰对远洋航运网络的功能可靠性影响明显；当f=0.76时，l值为0，此时网络中不存在任何连接；f ＞0.76后，整个网络便处于瘫痪状态。

（2）“多参数”标准下，s值快速下降，当f=0.35时，s值趋于0，即当35%的节点被干扰时，网络中已不存在联通子图，所有节点已处于孤立状态，所以，在按照综合标准下进行定向干扰对中国远洋航运网络的效率可靠性影响较大。

5.四种标准的定向持续干扰仿真结果的比较

四种标准的定向持续干扰仿真结果如图5-3-10所示。

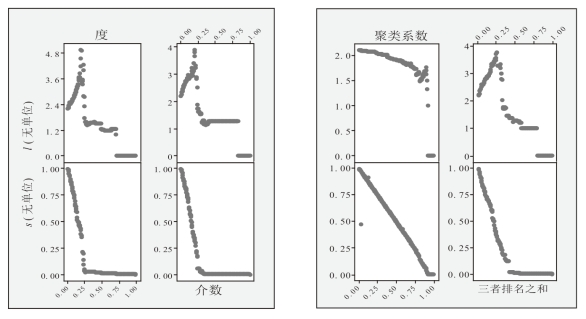
图5-3-10　四种标准的定向持续干扰仿真结果的对比

从图5-3-10可以看出：

（1）在四种不同的攻击标准中，l值均随着f的增加呈现出先增加后减少的变化趋势，最终都降为0。其中，按照度排序进行仿真时，l值得增幅和减幅最为显著。从图中可以看出，按照度排序仿真进攻时，l降为0的速度最快，当l值为0时 f=0.68，即整个网络中约68.8%的节点受到攻击时，整个网络中的节点全部孤立，节点之间无法联通。

（2）按照度排序对远洋航运网络进行仿真干扰时，l降为0最为迅速，说明度排序中的节点受到干扰时，对整个远洋航运网络的破坏最大，所以这些节点对于网络的功能可靠性有较为重要的作用。

（3）在按照度排序、介数排序、聚类系数排序以及度、介数和聚类系数之和排序进行攻击时，f的峰值分别为fc1=0.188，fc2=0.225，fc3=0，fc4=0.25，根据网络功能可靠性的度量标准，可知在度、介数和聚类系数之和排序进行攻击时，网络的功能可靠性最差，即该网络的中转能力受影响最大。

（4）从图5-3-10中不难看出，s值随着f值的增加都呈现出逐渐减小的趋势，其中按照聚类系数排序对网络节点进行干扰时，s值得减速最慢；在其他三种方案中，无论是按照度排序、介数排序或者三者排名之和排序进行干扰，s与l 的对应关系变化不明显。