5.1.1.1 模型基础
1.全要素生产率测算方法
全要素生产率测算主要是通过参数或非参数方法实现的。
参数方法中以索洛余值法、随机前沿生产函数法为代表。索洛余值法首先对生产函数的形式进行假设,接着依据该生产函数计算出产出增长率,然后将产出增长率与投入要素增长率之差作为全要素生产率的值。由于这种方法仅对生产函数进行了估算,对要素投入没有进行具体的分析,最终得到的生产率与实际情况难免会有出入。随机前沿生产函数法(Aigneretal.,1977)则在余值法的基础上,进一步对技术无效率的情况进行了分析,着重分析技术对产出的影响。但随着生产过程的复杂化,这种方法也显示出其弊端:首先,在生产函数假设环节上,由于这种假设并没有提前经过数据的拟合,相当于是先得到结果,再用数据条件进行检验,这样无疑会与实际情况存在偏差;其次,要得到较为准确的生产函数形式,就必须有大量的数据进行拟合,因此,对于小样本数据,随机前沿生产函数法拟合结果不够准确;再次,作为全要素生产率的参数估算法,就有着所有参数方法的共同局限性,即只能处理单产出的情况,对于存在非期望产出的物质生产过程无效。
非参数方法最具代表性的是数据包络分析法与指数法。既然是非参数,那么显然区别于参数方法中对生产函数的假设。其中数据包络分析法将线性规划与几何分析统一起来,在投入产出理论的基础上,首先构造一个线性凸面作为生产前沿面,通过估算物质生产过程中决策单元与生产前沿面的偏离程度,客观判断该生产过程是否有效。同时,由于数据包络分析法对决策单元整个生产过程进行了度量,因此可以对决策单元无效的原因进行解释。除此之外,正是由于数据包络分析法对生产前沿面的特殊估算方法,使得其能够将一个投入与多个产出相联系,这样就能对多产出问题的效率进行分析。指数法在原理上与数据包络分析法大致相同,唯一的区别在于不同的指数所采用的距离函数不同,也就是说在估算决策单元与生产前沿面的偏离程度方法上有所区别。如,Malmquist生产率指数是基于传统距离函数;Malmquist-Luenberger生产率指数是基于方向性距离函数。随着生产过程的复杂化和理论研究的深入,更多更为实用的方法被应用于全要素生产率测算中。
2.环境技术集
随着全要素生产率的发展,从产出角度来看,多数研究并没有考虑生产经济性产出的同时往往伴随着污染物的产生。但事实上,经济系统的物质生产过程,除了会得到人们希望的产出外,多少都会附带地产出一些人们不希望得到的负产品。传统的全要素生产率在输入端仅仅考虑了劳动、资本等要素的投入对产出的影响,忽略了输入端的资源环境以及输出端的环境污染也会对产出有很大程度的约束作用,对经济社会生产的经济及其他效应的衡量存在一定的偏差。
在意识到物质生产过程中的自然资源及环境污染对产出影响后,人们在分析方法上主要对其进行如下处理:一种方法是将污染物作为负的投入,这种投入越少,其对产出的影响也越小,产出效率也最大。具体做法是利用环境经济学理论将污染物作为生产过程中产生的非期望产出纳入生产函数当中,借助距离函数和线性规划直接求解出影子价格;另一方面将污染物作为正产出的附加负产出,这种产出越少越好,在效率测算过程中,如果将正产出与负产出分开来计算会将过程复杂化,因此一般会将负产出逆向化处理后与正产出进行统一计算。
钟等(Chungetal.,1997)将传统的生产技术扩展为环境生产技术,将“多投入—单产出”研究框架扩展到“多投入—多产出”的评价体系中,构造了ML生产率指数,为据包络分析法在环境领域的发展提供了理论基础。根据钟等(Chungetal.,1997)对环境技术集的定义,它是一个既包含期望产出(DesirableOutput)又包含非期望产出(UndesirableOutput)的生产可能性集合,即假设k=1,……,K个生产单位使用N种投入x=(x1,x2,…,xN)∈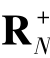 ,得到M种“好”产出y=(y1,y2,…,yM)∈
,得到M种“好”产出y=(y1,y2,…,yM)∈ 和I种“坏”产出b=(b1,b2,…,bI)∈
和I种“坏”产出b=(b1,b2,…,bI)∈ ,则环境技术集表示为:
,则环境技术集表示为:
![]()
其中,P(x)是生产集合,表示的是投入N种生产要素后能产生的所有“好”产品和“坏”产品的产量的所有生产可能性组合。上述x、y和b分别表示投入、“好”产出和“坏”产出的向量,“坏”产出主要是指生产过程中所排放的各种环境污染污染物,包括SO2、CO2、废水、废气和固体废物等。
该环境技术集可以通过一个线性规划来求解,即:
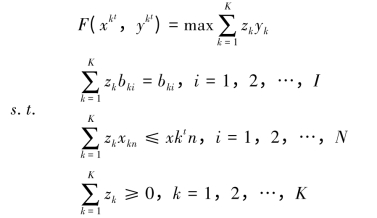
其中zk表示每一个决策单元的横截面观察值的权重,权重为正数表示生产技术为规模报酬不变。为了表示产出的零结合需要对上述模型强调以下两个条件:表示至少有一个国家或地区生产每一种环境污染等“坏”产出:每一个国家或地区都至少生产一种“坏”产出,用公式表示为:
![]()
3.方向性距离函数
Chambers,Chung和Fare(1996)将谢泼德产出距离函数一般化,提出了非径向的方向性距离函数,同时在环境技术集的基础上,构造了一个产出角度的方向性距离函数法,能够识别出环境污染等非期望产出不同于“好”产出的负外部性,能够同时实现“好”产出的扩张和“坏”产出的减少。其表达式如下:
![]()
其中,g表示产出扩张的方向向量。该方向向量的选择并不是唯一的,根据研究者的研究需要不同而选择。如下图形5—1中所示,方向向量有如下的三种情况:第一,方向向量g=(y,0)并且在构造生产技术时不考虑非期望产出,表示没有环境管制的存在;第二,方向向量g=(y,0),表示在环境规制存在的情况下,期望产出增加而非期望产出保持不变;第三,方向向量g=(y,-b),表示在投入要素给定的情形下,沿着方向向量期望产出成比例的扩大,而非期望产出成比例的缩小。(https://www.xing528.com)
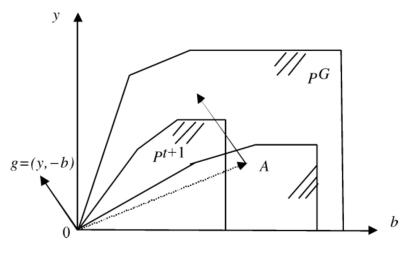
图5—1 包含期望产出与非期望产出的方向性距离函数
在本书的研究中,假设方向向量为第三种形式,即在投入要素给定时,期望产出沿着方向向量g=(y,-b)成比例的扩大,且非期望产出成比例的缩小。进而方向性距离函数转化成为如下表达形式:
![]()
同样地,该方向性距离函数可以通过DEA来求解,需要求解下面的线性规划:

5.1.1.2 SBM方向性距离函数
上述基于径向和角度方向性距离函数的DEA模型由于没有考虑松弛性问题,对效率的测算在一定程度上会存在失真现象。为了更准确地对效率进行测算,Tone(2001)提出了SBM(Slack-basedmeasure)效率测度模型。SBM模型的方向性距离函数是非径向非角度的,这样就能在避免松弛和角度问题的同时对存在非期望产出的效率进行测算。本书即采用这种方向性距离函数模型对中国工业生态化效率进行静态测算。SBM方向性距离函数形式如下:
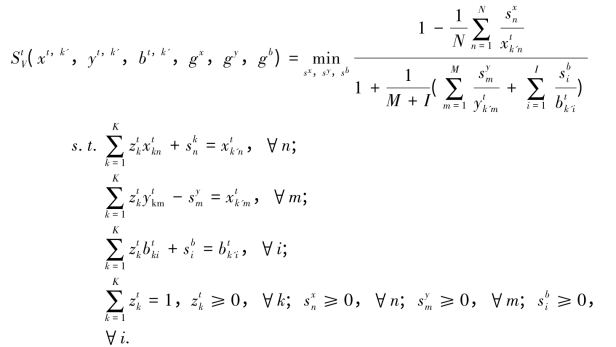
式中N、M、L分别为投入、期望产出和非期望产出个数;(xt,k',yt,k',bt,k')表示t时期第k‘省份工业投入和产出的方向向量;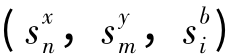 表示投入、产出的松弛向量;
表示投入、产出的松弛向量; 表示决策单元的权重。目标函数
表示决策单元的权重。目标函数 表示生产技术为可变规模报酬(VRS)条件下的产业生态化效率,它关于
表示生产技术为可变规模报酬(VRS)条件下的产业生态化效率,它关于 严格单调递减,且0<
严格单调递减,且0< ≤1。若
≤1。若 =1,表示工业生态化过程是完全有效的,投入产出也不存在损失的情况;若
=1,表示工业生态化过程是完全有效的,投入产出也不存在损失的情况;若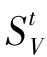 <1,表示产业生态化效率存在损失,若要达到完全有效,投入与产出仍需优化。另外若没有
<1,表示产业生态化效率存在损失,若要达到完全有效,投入与产出仍需优化。另外若没有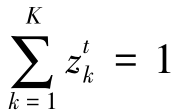 的约束条件时,采用同样的方法可计算不变规模报酬(CRS)下的产业生态化效率
的约束条件时,采用同样的方法可计算不变规模报酬(CRS)下的产业生态化效率 。
。
在对效率值进行测算的基础上,还可以对效率损失进行分析,按照公式将生态效率的损失部分进行分解,具体形式如下:
![]()
其中,投入无效率:

期望产出无效率:

非期望产出无效率:
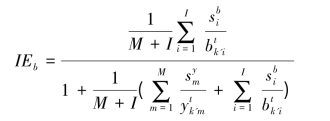
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




