经理人个人财富变量定义及计算方法

上市公司样本中经理人的薪酬变量包括以下三项：经理人的货币薪酬（Φd），取自2016年度经理人固定工资与津贴的总额；经理人的持股比例（），由2016年公司年报披露的经理人年末持股数除以总股本计算而得；经理人持有股票期权比例（），根据公司历史上的所有股权激励计划行权记录，计算得出经理人在2016年底持有的期权数量，除以总股本即得到持有股票期权比例。此外，由于经理人实际个人财富数据不可观测，本书基于2011—2016年间薪酬数据进行估算。具体而言，根据每一年年报披露的经理人固定工资与津贴收入，计算出当年的税后净收入。^[1]假设经理人的年度净收入（yn）于每年年末获得，期间不消费并全部投资于无风险债券获取年度无风险收益（r0），下标n代表相对于2016年的年份，如2016年n取值0，以此类推，2011年n取-5。2016年末经理人个人财富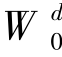（）为：

上市公司股票市场变量包含以下四项：公司总市值（P0）、公司总股本（B0），来自公司2016年年末的数据；公司股票的历史波动率（σ），本书采用2016年1月1日至2016年12月31日的个股周对数收益率计算年度历史波动率；无风险利率（r0），由于样本中经理人的代表性期权的到期日T在2年左右，本书选用2016年底2年期国债收益率2.29%。由于后文计算中将用到的连续复利下的年度无风险利率，在此根据rf＝ln（1＋r0）进行转换，得到连续复利下的无风险利率为2.264%。需要指出的是，由于上市公司在股利分配时也会相应地调整股票期权的行权价格和行权数量，因此上市公司的分红行为以及股息率的存在并不会对期权价值、期望效用和激励产生实质性的影响，本书假设股息率为零，即不考虑股利分配产生的影响。

由于部分上市公司会给经理人多个股票期权激励方案，因此经理人实际上持有多份股票期权。本书根据公司历史上所有股权激励计划以及具体行权明细，计算了2016年末经理人持有的有效期权（未到期且未全部行权），其中第i份期权占总股本的比例为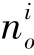。此外，部分经理人持有的期权组合包含不同行权价格和不同到期日的多种期权，而本书的模型只考虑单一的到期日，因此需要将这一系列期权处理成一个代表性期权。本书利用Core and Guay（2002）提出的单一近似法（OA Method）构造“代表性期权”，构造出的这一期权可以以很小的偏差模拟出原期权组合近99%的波动特征。具体构造思路如下：确定代表性期权的行权价格（K）和到期日（T），使得代表性期权的市场价值（BS）以及期权价值对标的资产价格波动的敏感性（Delta）与被估计的多份期权构成的期权组合相同。记nO为经理人持有股票期权的比例，表示第i份期权的比例，Ti表示i份期权的到期日，Ki表示第i份期权的行权市值，本书按照方程组（5-19）式与（5-20）式计算代表性期权的特征。由于该方程组含有两个方程和两个未知数：代表性期权的行权价格（K）和到期日（T），因此可以直接求解出两个未知数的取值。此外，考虑到虽然经理人可以在期权到期日内的任一时刻行权，但事实上所有经理人都会在期权到期日之前行权，因此本书参照Dittmann and Maug（2007）的方法，在计算出的代表性期权到期日（T）的基础上乘以0.7。

(www.xing528.com)

经理人效用函数的参数包括以下几项：常相对风险厌恶型函数下的参数γ；以及损失厌恶型效用函数下的参数α、参数β、参数λ。参照现有研究的惯例（Dittmann and Maug，2007），将经理人的风险厌恶系数设置为γ＝3；根据Tversky and Kahneman（1992）的实验结果，选取α＝β＝0.88，λ＝2.25作为研究的基准参数。对于参考薪酬WR，由于价值函数并未给出参考薪酬的取值，假定经理人的参照薪酬取决于前一年的薪酬水平，即2015年的货币薪酬（Φ-1）、股票（nS-1）与期权（nO-1）。具体由以下公式计算参考薪酬WR（θ）＝Φ-1＋θMV（nS-1，nO-1，P0），其中参数θ∈［0，1］表示经理人将前一期证券价值计入参考薪酬的贴现因子，MV表示前一期证券持有至当期的市场价。首先，经理人的参考薪酬不会低于2015年的货币薪酬（固定工资与福利津贴之和），即经理人肯定会将未来总薪酬低于2015年货币薪酬的情况视为损失，因此，本书将2015年的货币薪酬Φ-1为参考薪酬的下界（θ＝0）。其次，经理人也很可能将其2015年末持有的股票nS-1和股票期权nO-1作为参考薪酬的一部分，当然，由于经理人并未进行分散投资，他会将这一部分股票和期权的市场价值贴现计入参考薪酬。因此对于参考薪酬的上界，本书将经理人2015年的货币薪酬，与经理人持有2015年末的股票和股票期权到2016年末的市值进行加总，并根据经理人在2016年交易股票的情况对这一总和进行调整（θ＝1）。

表5-1　变量定义表

续　表