市场均衡下的薪酬水平分析

用w（N）代表市场中才能最低的经理人（n＝N）的保留工资，求解微分方程（3-4）可得：

为了进一步求解工资函数（3-5）式的具体形式，必须对公司规模S（.）以及经理人才能T（.）的函数形式作假设。本书假设公司规模服从指数为1／α的帕累托分布：

根据齐普夫定律（Zipf's Law），参数α取值接近于1，Axtell（2001）与Gabaix and Landier（2008）的实证结果也证实了美国公司规模的分布符合齐普夫定律。在下节中我将根据中国公司实际数据测度参数α。然而，对于经理人才能函数的分布T′（u），却鲜有理论与现实的证据。我参照Gabaix and Landier（2008），基于极值理论（extreme value theory，EVT）对经理人才能的分布函数进行设定。根据极值理论，对于所有常规的连续性分布，包括均匀分布、高斯分布、指数分布、对数正态分布、帕累托分布等，存在常数β和B，使得分布函数的右尾部（极值）服从函数（3-7）式的设定：

根据大数定律，经济体中所有注册公司经理人的才能分布应服从正态分布。那么对于才能较高的上市公司经理人这个群体（如选择500家规模最大上市公司的经理人），他们的才能位于总体（全国有数千万家注册公司）经理人才能分布的右尾，满足极值理论。通过方程（3-7）式的假定，可以将方程（3-5）式的显示解刻画出来，进而讨论经理人均衡薪酬水平的诸多特点。

将方程（3-6）（3-7）式代入（3-5）式，可得：

当只考虑全体公司中规模最大的一小部分公司（数千万家公司中最大的500家）时，n／N→0。因此，相对于n-（αγ-β），N-（αγ-β）和w（N）都非常小，方程（3-8）式可近似于：(www.xing528.com)

考虑一家参照公司，如500家最大的上市公司的中位数，排名第250位的公司n*，其规模为S（n*）。由此可以推导出“均衡市场中经理人薪酬水平定理”：才能排名n的经理人受雇于规模排名n的公司S（n），并且获得方程（3-10）式所示的均衡工资水平。

其中，D（n*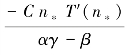）＝是独立于公司规模的常数。特别地，对于参照公司，其经理人薪酬水平为w（n*）＝D（n*）S（n*）γ。等式（3-10）意味着经理人薪酬水平不仅取决于所在公司的规模，也就是经理人自身才能水平，也跟整体市场需求有关（参照公司规模），即市场对经理人才能的总需求。

根据“均衡市场中经理人薪酬水平定理”，可得出以下两条关于经理人薪酬的预测以供后续实证检验：

（1）横截面预测：给定年份中，经理人薪酬水平与公司规模的γ-β／α次方成比例，即w（n）∝S（n）γ-β／α。

（2）时间序列预测：随时间变化，当所有公司规模增加λ倍，所有公司经理人薪酬水平也相应增加λγ倍，即w′（n）＝D（n*）［λS（n*）］β／α［λS（n）］γ-β／α＝λw（n）。