二氧化碳排放与煤炭资源配置的关系分析

二氧化碳排放空间配置状况，要靠二氧化碳排放量来衡量，而二氧化碳的排放主要来自化石能源的消费。在中国化石能源的消费中，则主要以煤炭的消费为主，其消费占能源消费总量的比例常年维持在70%左右，^[4]因此，煤炭资源的配置可能对中国工业部门碳排放空间配置结构具有重要的影响。本小节将对二氧化碳排放空间配置与煤炭资源配置之间的关系进行详细的实证分析。

1.经济计量模型、变量及数据说明

使用的数据为中国工业部门1999—2011 年36 个两位数行业的能源消费面板数据，^[5]用二氧化碳排放空间配置比例作为被解释变量；用各两位数行业煤炭资源消费占整个行业的比例来代表煤炭资源配置状况，并将其作为解释变量。建立如下的面板数据模型：

式中，i 代表两位数行业，t 代表年份（1999，2000，…，2011），λi和ηt分别代表个体效应和时间效应，α0代表截距项。lncarbon＿pit和lncoal＿pit分别为某两位数行业二氧化碳排放空间配置比例和煤炭资源配置比例的对数。β 代表二氧化碳排放空间配置比例对煤炭资源配置比例的弹性系数，即煤炭资源配置比例变动1%时，二氧化碳排放空间配置比例变动的百分比。

2.面板单位根检验

同模型（5.8）一样，所采用的面板单位根检验方法仍为LLC 检验，具体结果见表5.10。从表5.10 中的单位根检验结果来看，模型（5.12）中各变量均为平稳变量，因此可以直接进行模型的设定检验。

表5.10　面板单位根检验结果

3.模型设定检验

从表5.11 中的Hausman 检验结果来看，在α ＝0.05 的显著性水平下，高度拒绝了原假设，表明模型（5.12）为固定效应模型，为此需要继续对固定效应模型中个体、时间或个体时间固定效应影响的显著性进行检验。

表5.11　Hausman 检验结果

对于固定效应影响的显著性检验，本书基于Hendry 的“一般到特殊”的建模思想，采用无约束模型和有约束模型的回归残差平方和之比构造F 统计量，以检验固定效应模型的合理性。以个体固定效应的影响为例：首先，对有约束模型（混合数据回归模型）进行估计，得到残差平方和为RRSS；其次，对无约束个体效应模型进行估计，得到残差平方和为URSS，则在零假设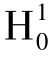：λ1＝λ2＝λ3＝… ＝λN－1＝0 下，可以构造如下F 检验统计量：

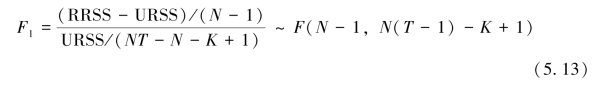
式中，K 为个体固定效应模型待估参数的个数，N 为个体个数，T 为时期数。在给定的显著性水平下，如果拒绝了零假设，则模型设定为个体固定效应模型是合理的。

类似于个体固定效应模型的设定检验，时间固定效应模型的设定检验本书也采用无约束模型和有约束模型的回归残差平方和之比构造F 统计量。F 检验的零假设是：

在零假设下F 统计量为：

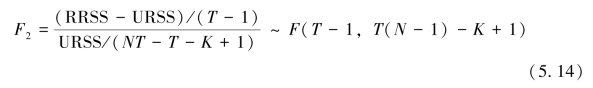
在给定显著性水平下，如果拒绝了零假设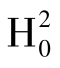，则将模型设定为时间固定效应模型是可行的。

对于个体时间固定效应，F 检验的零假设分别是：(www.xing528.com)

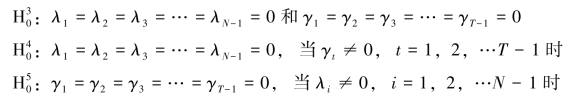
在假设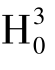下，

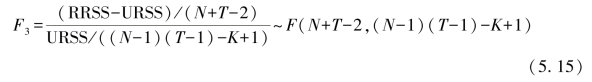
在给定显著性水平下，如果拒绝了零假设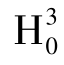，则将模型设定为个体时间固定效应模型是可行的。

同样，在下，

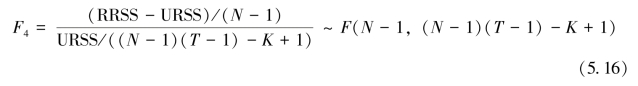
在给定显著性水平下，如果拒绝了零假设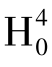，则在存在时间固定效应的情况下，模型也包含个体固定效应，即将模型设定为个体时间固定效应模型是合理的。

同样，在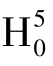下，

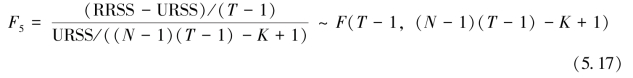
同理，在给定显著性水平下，如果拒绝了零假设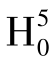，则在存在个体固体效应的情况下，模型也包含时间固定效应，即将模型设定为个体时间固定效应模型是合理的。

表5.12 给出的模型（5.12）的固定效应显著性检验结果表明模型的时间固定效应在给定α ＝0.05 的显著性水平下不显著，模型应为个体固定效应模型。

表5.12　固定效应显著性检验结果

4.估计结果分析

由于本书所采用的数据为大N 小T 型面板数据，因此其具有截面数据的特征，需要对其进行组间异方差检验。检验结果显示（见表5.13），模型存在显著的组间异方差，为了使估计结果可靠，这里采用稳健型估计来考量参数的显著性（见表5.14）。为了进行比较，这里也列出了OLS 的估计结果（见表5.15）。

表5.13　组间异方差检验结果

表5.14　稳健型估计结果

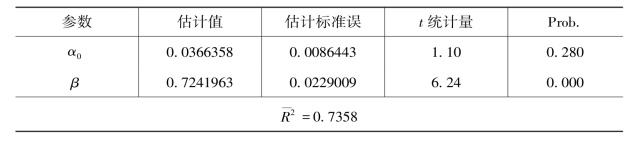
表5.15　OLS 估计方法结果

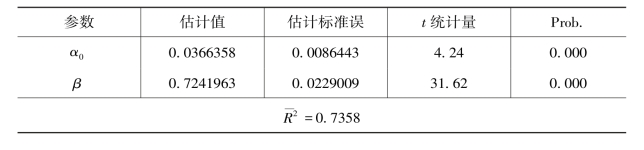
从表5.14 和表5.15 中的估计结果可以看出，两种估计方法所得的参数估计值并没有差别，只是稳健型估计的模型的标准误有所增加，因而其估计出的参数的显著性更加保守。采用稳健型估计的结果，可以看出煤炭资源配置比例的变化对二氧化碳排放空间配置有显著的影响。具体来讲，煤炭资源配置比例每增加1%，二氧化碳排放空间配置就会增加0.72%。因此，如果想要降低本行业的二氧化碳排放空间配置比例以提高碳生产率，降低煤炭资源配置比例（从另一个角度来讲就是降低煤炭资源的消费）显得尤为重要，这个结论与我们的主观感受恰好吻合。