识别中国工业部门碳生产率变化的内部机制

1.经济计量模型、变量及数据说明

使用的数据为中国工业部门1999—2016 年36 个行业面板数据，以模型（5.7）为基础，将全要素生产率框架下的碳生产率指数作为被解释变量，劳动力要素、资本要素和二氧化碳排放空间要素的配置比例作为解释变量，得到如下面板数据模型：

模型（5.8）中，i 代表各两位数行业，t 代表年份（ t ＝1999，2000，…，2016）；λi为个体效应，用来控制工业部门各两位数行业的特有性质，不随时间变化，在截面间相互独立；α0代表截距项；εit为随机误差项，ηt代表时间效应。

lnM＿Pit表示第i 个行业的碳生产率指数的对数；labor＿pit、Capitical＿pit和carbon＿pit分别表示第i 个行业劳动力、资本和二氧化碳排放空间占整个行业的比例，用以反映各投入要素在各行业的配置比例；β1、β2和β3分别表示资源配置比例变动的弹性系数，即当各资源配置比例分别变动1%时，碳生产率指数变动的百分数。如果有一个参数为负，那么这个变量则成为抑制各两位数行业碳生产率提高的因素，同时也有可能成为解释中国工业部门碳生产率指数差异自动消除的原因。

全要素生产率研究框架下的碳生产率指数（M＿P）的数据由本书第三章利用基于方向性距离函数的DEA 方法测算而得；劳动力要素配置比例数据（各行业从业人员占工业部门全部从业人员的比重）由历年《中国统计年鉴》中的数据计算而得；资本要素配置比例数据（各行业固定资产净值的占工业部门全部固定资产净值的比重）由历年《中国统计年鉴》中的数据计算而得；二氧化碳排放空间要素配置比重（各行业碳排放量占工业部门总体碳排放量的比重）由第三章中的估算数据整理计算而得。

2.面板单位根检验

为了避免模型由于非平稳数据的采用而造成“伪回归”问题，在进行模型的设定前，需要对面板数据的平稳性进行检验，这就要求我们首先对模型中所涉及的变量进行面板单位根检验。

面板单位根检验理论上不断有新的成果出现，目前仍存在诸多争议。各种检验方法各有优势与不足。面板单位根的检验方法主要有Sarno 和Taylor（1998）检验、IPS（Im，Pesaran and Shin，2003）检验、Fisher-PP 和Fisher-ADF 法（Maddala and Wu，1999）检验、LLC（Levin，Lin and Chu，2002）检验，下面对这几种常用的检验方法进行一个简单的比较。

Sarno 和Taylor 检验，在估计过程采用“似无相关模型（SURE）”，因此适用于大T 小N 型（截面数小于时间序列数）面板数据的单位根检验，而且该检验允许每个截面有不同的滞后阶数，但这些滞后项的系数之和在原假设下等于1（Taylor，M.P.，L.S.，1998）；Im，Pesaran 和Shin 考虑了截面异质性（heterogeneous panels）和干扰项的序列相关问题，对单个截面执行ADF 检验后得到了t 值的平均值，但其局限在于要求面板是平行的（balanced）（H.Pesaran，2007；K.S.Im，M.H.P.，Y.Shin，2003）；Fisher 检验以个体单位根检验的p 为基础构造统计量，其优点在于适用于非平行面板（Maddala，G.S.，W.Shaowen，1999）。

上述四个面板单位根检验的原假设H0均为：面板中的所有截面对应的序列都是非平稳的。结果如果拒绝原假设，并不表明所有序列都是平稳的，只能保守地说至少一个序列是平稳的。

与上述检验不同，Levin，Lin 和Chu（2002）检验假设所有序列均服从AR（1），且相关系数相同，但允许存在个体固定效应；对单个截面执行ADF检验后得到t 值的平均值，并作相应调整后得到检验统计量。该统计量在H0下服从正态分布，若H0被拒绝，则认为所有序列均平稳，这是与其他几个检验方法的不同之处；同时，该检验估计过程采用固定效应模型，因而适用于大N 小T 型面板数据的检验（Levin，A.，Lin，Chien-Fu and Chia-Shang James Chu，2002）。

本书所采用的面板数据为典型的大N 小T 型面板（N ＝36，T ＝18），故采用Levin，Lin 和Chu 检验对模型（5.8）中涉及的变量进行面板单位根检验，应用STATA12.0 中的levinlin 命令进行单位根检验，得出了如表5.4 所示检验结果。从表5.4 中单位根检验的结果来看，各变量均为平稳变量，因此可以直接进行模型的设定检验。

表5.4　面板单位根检验结果

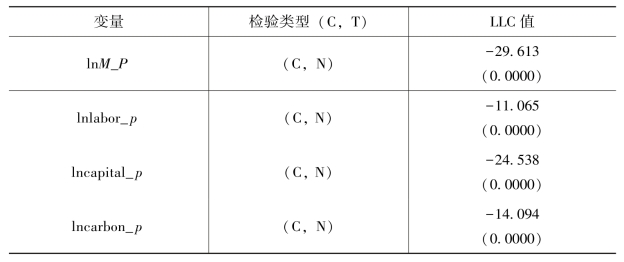
注：检验形式（C，T）分别代表截距项、趋势，“N”为没有相应项，滞后项按照SIC信息准则确定。

3.模型设定检验

模型设定检验的目的是确定模型是固定效应模型还是随机效应模型。固定效应模型包括：个体固定效应模型、时间固定效应模型和个体时间固定效应模型。随机效应模型包括：个体随机效应模型和个体时间随机效应模型。

对于模型是固定效应还是随机效应的检验，通常采用Hausman 检验来确定。Hausman 检验的基本思想为：如果效应与解释变量不相关（即Corr（u＿i，x＿it）＝ 0），那么随机效应和固定效应得到的估计都是一致的，但随机效应模型更有效；如果效应与解释变量相关（Corr（u＿i，x＿it）≠0），固定效应模型仍然有效，但随机效应模型估计是有偏的。Hausman（1978）提出了一个检验统计量：

在原假设成立的情况下，H 渐进服从χ2（K）分布，K 为模型中解释变量的维度。

如果拒绝原假设，则模型应该为固定效应模型，为此就可以进一步对模型是个体固定效应、时间固定效应还是个体时间固定效应进行显著性检验。如果接受原假设则意味着采用随机效应模型比较有效，继而可以对模型中个体和个体时间随机效应影响的显著性进行检验。

首先，对模型（5.8）是固定效应模型还是随机效应模型进行检验，检验结果（见表5.5）表明，在α ＝0.05 的显著性水平下，接受了原假设，说明采用随机效应模型更有效。为此可以继续对随机效应模型中个体和个体时间随机效应的显著性进行检验。

表5.5　Hausman 检验结果

个体随机效应显著性检验采用Breusch-Pagan 检验，其检验思想为：若约束是有效的，那么最大化拉格朗日函数所得到的有约束的参数估计量应该位于最大化原始样本似然函数的参数估计值附近。因此，该处对数似然函数的斜率应该趋近于0。Breusch-Pagan 检验就是在有约束的参数估计量处，通过检验对数似然函数的斜率是否趋近于0 来检验约束是否有效。Breusch 和Pagan（1980）通过构造Lagrange 乘数统计量来检验随机效应的显著性。

（1）检验个体随机效应的显著性(www.xing528.com)

原假设和备择假设是：

LM 统计量为：

在零假设下，统计量LM 服从1 个自由度的χ2 分布，即LM ～χ2（1）。拒绝原假设则应该建立一个个体随机效应模型。

（2）检验个体时间随机效应的显著性

原假设和备择假设是：

LM 统计量为：

零假设下，统计量LM 服从2 个自由度的χ2 分布，即LM ～χ2（2）。拒绝原假设则应该为个体时间随机效应模型。表5.6 给出了模型（5.8）的随机效应显著性检验结果，表明模型为个体时间随机效应模型。

表5.6　随机效应显著性检验结果

4.估计结果分析

模型（5.8）的估计结果见表5.7。结果显示，有两个参数高度不显著，因此需要对模型估计的异方差性、序列相关性和截面相关性进行检验。由于随机效应模型本身已经较大程度地考虑了异方差性问题，因此仅对其序列相关性进行检验。

表5.7　OLS 估计方法结果

表5.8 的检验结果显示，随机效应模型存在显著的一阶序列相关性，因此我们需要使用广义最小二乘法（GLS）进行估计，估计结果见表5.9。

表5.8　序列相关检验结果

表5.9　GLS 估计方法结果

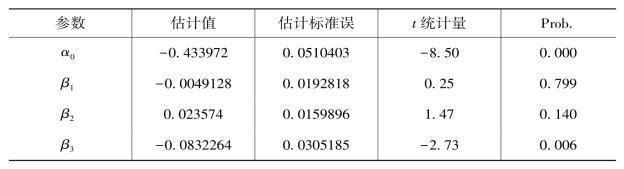
从表5.9 的估计结果来看，广义最小二乘法估计结果的参数的显著性有明显提高，这里以广义最小二乘法估计结果进行分析。表5.8 的估计结果显示：劳动力资源配置和资本配置比例变动的弹性系数均不显著，表明在中国工业部门碳生产率指数变化过程中，劳动力要素配置比例和资本要素配置比例的变动不是最重要的因素（注：这并不表明劳动力要素与资本要素配置比例的变化对碳生产率的变化没有影响）；而二氧化碳排放配置比例变动的弹性系数为－0.08，并且高度显著，表明中国工业部门各两位数行业之间二氧化碳排放空间配置比例的变动是碳生产率指数变动的重要原因。

具体来讲，二氧化碳排放空间配置比例变动的弹性系数为负，表明各两位数行业i 的二氧化碳排放空间要素在整个工业部门的二氧化碳排放空间要素配置中所占比例每提高一个百分点，其碳生产率指数就下降0.08 个百分点。这一结果说明：①二氧化碳排放空间配置比例的增加会抑制碳生产率的增长速度；②二氧化碳排放空间要素的再配置是中国工业部门碳生产率δ- 收敛和绝对β-收敛的一个重要的形成机制。

在各两位数行业之间，由于劳动力、资本以及二氧化碳排放空间要素配置比例的不同，形成了各两位数行业不同的经济增长速度，进而导致了碳生产率指数的差别。从实证结果看，劳动力和资本要素的再配置对碳生产率指数的影响不明显，在此主要分析二氧化碳排放空间要素在各行业之间流动对碳生产率指数变化的影响机制。假设劳动力和资本要素在各行业之间的配置比例不变，那么二氧化碳排放空间要素则从经济产出效率低的部门流向经济产出效率高的部门。二氧化碳排放空间要素配置比例的减少使得经济产出效率低的部门碳生产率指数增加，而二氧化碳排放空间要素配置比例的增加则使得经济产出效率高的部门碳生产率指数降低，因此形成了中国工业部门碳生产率指数的δ- 收敛和绝对β-收敛。

根据以上分析可以得出如下结论：从内部机制来看，各两位数行业降低本部门的二氧化碳排放空间配置比例是提高本部门碳生产率的一条重要途径，而降低二氧化碳排放配置比例的解决方案需要我们进行进一步的探讨。