门槛回归模型：传统方法的不足及Hensen提出的新思路

对于时间序列数据，如果变量间的关系随着时间的推移发生变化，则需要将样本一分为二（或更多）分别进行回归，划分的标准被称为门槛（门限）值（threshold level）。传统的做法是，研究者主观（随意）设定一个门槛值，既不对门槛值进行参数估计，也不对其显著性进行统计检验。这样做显然是不可靠的。为此，Hensen（2000）提出了“门槛（门限）回归（threshold regression）”，并以严格的统计推断方法对门槛值进行参数估计和假设检验[26]。门槛回归模型的基本形式为：

样本数据为，其中qi为用来划分样本的“门槛变量（threshold variable）”，qi可以是解释变量xi的一部分，也可以是其他影响因素，γ 为待估的门限值，xi为外生解释变量，与扰动项εi不相关。可以将以上分段函数合并写成：

其中，1（·）为示性函数，即如果括号中的表达式为真，则取值为1；反之，取值为0。在一定条件下Hensen 导出了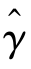的大样本渐进分布，在此基础上构造出了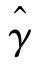的置信区间，并对H0：γ ＝γ0的原假设进行了似然比检验。

根据Hensen 的门槛回归原理，工业化率、城镇化率与工业部门碳生产率的关系可以设定为如下形式：(www.xing528.com)

其中，ICPt代表工业部门碳生产率，RIt代表工业化率（%），URt代表城镇化率（%），εt为随机误差项，t 代表时间。将模型（4.3）变形为如下对数模型

那么，模型的参数η1就表示工业碳生产率对工业化率的弹性，η2就表示工业碳生产率对城镇化率的弹性。