检验碳生产率的β收敛性

1.模型设定

一般认为，真正意义上采用计量方法实证检验经济增长收敛性假说的研究工作起源于Baumol（1986），他建议用如下回归方程来检验经济增长的收敛性。

gi表示第i 个经济体的年均经济增长速度，Yi，o表示第i 个经济体起初的经济状态，εi为随机扰动项，服从正态分布。回归系数β 表示经济的收敛性，如果回归系数的估计值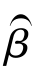显著为负，则意味着不同经济体之间存在收敛特征，该方法本质上是检验绝对β-收敛性的方法。

之后，Barro 和Sala-I-Martin（1991）发展了Baumol 的简单回归方法并提出了如下的回归模型：

Yi，o和Yi，r分别表示经济体i 期初和期末的经济状态，T 表示时间跨度，α为常数，β 仍然为收敛速度，其取值依然取决于期初的经济状态，因此检验的仍为绝对β-收敛性。

Atkins 和Boyd（1998）提出了一种更为简单的检验是否存在绝对β-收敛性的回归方法：

这里β 的估计值小于1，则表明经济体之间存在绝对β- 收敛性。Seungjin，Sim（2004）、Fallon 和Lampart（1998）、Persson（1997）、刘强（2001）、魏后凯（1997）等均使用这种检验方法做过收敛性研究。

本书采用Atkins 和Boyd 所提出的计量模型对中国工业部门是否存在绝对β-收敛性进行检验。首先，设时间间隔为1 年，则模型（3.11）可变形为如下面板模型：

式中i 代表中国工部门各两位数行业，t 代表年份（t ＝1999，2000，…，2016）；εi，t为随机扰动项。α0为常数项；μi和ηt分别表示个体效应和时间效应；lnM＿Pi，t表示碳生产率指数的对数；β 为待估参数，若其估计值小于1，则表明我国工业部门各两位数行业的碳生产率指数之间存在绝对β-收敛性。

2.模型估计及结果分析(www.xing528.com)

模型（3.12）包含被解释变量的滞后变量lnM＿Pi，t－1，因此模型会产生内生性问题。因为，lnM＿Pi，t是μi的函数，显然lnM＿Pi，t－1也是μi的函数，所以lnM＿Pi，t－1就和误差项相关即corr（lnM＿Pi，t－1，μi）≠0，这就使得即使εit不存在序列相关，最小二乘（OLS）估计量也是有偏的和不一致的。因此，需要将个体效应μi去除。

Anderso 和Hisao（1981）建议首先对模型进行差分以剔除μi，然后使用D.yi，t－2＝yi，t－2－yi，t－3或yi，t－2作为D.yi，t－1的工具变量，只要εit本身不存在序列相关，这些工具变量就和D.εi，t＝εi，t－εi，t－1不相关。尽管这种工具变量估计法可以得到模型参数的一致估计，但不一定为有效估计，因为它没有利用所有可用的矩条件，而且也没有考虑误差项差分D.εi，t的结构。Arellano 和Bond（1991）在Anderson 和Hisao 所提出的矩（IV）估计的基础上增加了更多可用的工具变量，提出了一阶差分GMM（广义矩估计）估计量。但这种方法受弱工具变量的影响较大，易产生有限样本偏误。鉴于此，Blundell 和Bond（1998）提出了系统GMM 估计，系统GMM 估计结合了差分方程和水平方程，并且还增加了一组滞后的差分变量作为水平方程的工具变量。总的来说，系统GMM 估计具有更好的有限样本性质。

在此，分别列出差分GMM 和系统GMM 的估计结果，见表3.7、表3.8。

表3.7　模型（3.12）的差分GMM 估计结果

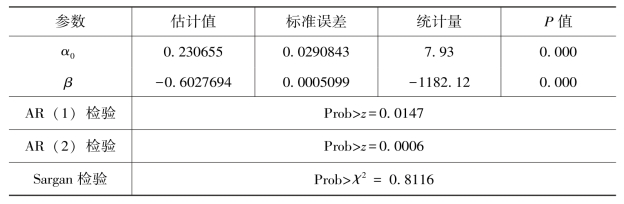
表3.8　模型（3.12）的系统GMM 估计结果

由表3.7、表3.8 的估计结果可知，利用差分GMM 和系统GMM 估计方法所得β 的估计值有所差异，但均小于1，并且高度显著。但差分GMM 和系统GMM 的二阶序列相关检验结果都显示，所选取的工具变量不合理。本节检验的为碳生产率指数的绝对β-收敛性，因此可以通过增加滞后期数对模型进行重新估计。

经过对滞后期的改变，发现模型滞后3 期后，效果比较理想，则模型（3.12）变形为模型（3.13），具体估计结果见表3.9。

表3.9　模型（3.13）的系统GMM 估计结果

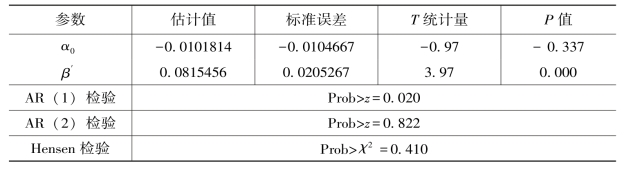
表3.9 中二阶序列相关和过度识别检验结果表明，所选工具变量合理。β′的估计值小于1，且高度显著，表明中国工业部门各两位数行业碳生产率指数之间存在3 阶段的绝对β-收敛性。