基于方向性距离函数的碳生产率测量模型

由于索洛余值法的假设条件在现实生产实践中很难满足，因此在进行测算方法的选择过程中不予考虑，主要从SFA 方法和DEA 方法中进行选择。从方法的本质来说，SFA 方法和DEA 方法在分析结果方面具有一致性，但由于两种方法是对效率不同特性和侧面的描绘，其差异也非常明显（顾乾屏等，2007）。鉴于DEA 方法不需要对函数形式进行设定，且无须要素的价格信息，故本书选择DEA 方法，在全要素生产率的研究框架下对中国工业部门碳生产率进行测算。

在运用DEA 方法对碳生产率进行测算的过程中，需要对各种模型进行选择。如果用传统C2R 模型对碳生产进行测算，测算结果为维持既定产出下中国工业部门各两位数行业二氧化碳排放空间投入的最大削减率，其主要关注减排目标的实现，而没有考虑另一个重要目标——产出增长目标。然而在当前和今后相当长一段时期内，产出的增长仍然是中国工业部门重要的宏观经济目标，而二氧化碳排放空间投入的大量削减有可能对中国工业部门潜在的产出增长产生负面影响。同时，该模型只能将二氧化碳排放空间作为诸多生产要素中的一种直接加入模型中进行计算，不能够同劳动和资本两种生产要素进行区分。在这种情况下，测算的生产率并不能体现二氧化碳排放空间要素的个体特征，只是在传统的全要素框架下加入了二氧化碳排放空间的投入，所测算出的生产率指数值称为碳生产率指数，也可以称之为资本生产率指数或劳动生产率指数。为解决上述不足，本书将借助于方向性距离函数来测度中国工业部门碳生产率指数。

目前还没有学者运用方向性距离函数在全要素生产率的研究框架下对碳生产率进行测算，但是已经有很多学者运用它来测度环境效率、生产率和全要素能源效率（Weber and Domazlicky，2001；Jeon，et al.，2004；Arcelus and Arocena，2005；Watanabe and Tanaka，2007；王兵等，2008；涂正革，2008；胡鞍钢等，2008；吴军，2009；陈茹等，2010；王兵等，2010，2011）。

方向性距离函数由Chambers 等（1996）提出，这种函数可以综合考虑产出的提高和投入的减少，与前文所述的低碳经济的两大目标（经济增长和二氧化碳排放量的减少）相吻合。

本研究把每一个两位数行业看作一个生产决策单位（DMU）来构造每一个时期中国工业部门生产的最佳时间边界，将二氧化碳排放空间同传统的投入要素等同对待一起纳入生产前沿面的构造中。假设每一个两位数行业使用N种投入，得到M 种产出；在每一个时期，第k ＝1，…K 个两位数行业的投入产出值为（xk， t，yk， t），在凸性、锥形、无效性和最小性的公理假设的前提下，参照Färe 等（2004）对生产技术集的定义，本书可将生产技术集表示为：

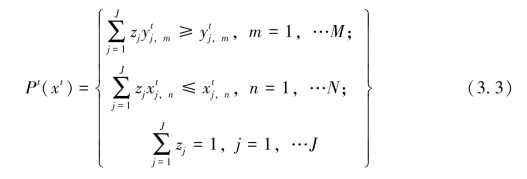
zj表示每一个横截面（每一个两位数行业）观察值的权重，非负的权重变量之和等于1 表示生产规模报酬是可变的。产出和投入变量的不等式约束表示产出与投入可自由处置。那么，可将方向性距离函数定义为：

其中（－ gx，gy）为方向向量，方向性距离函数可以按照既定方向实现产出的最大扩张和投入的最大削减。β 是标量，其值越大，效率越低，若β ＝0，则说明样本观察值已经在生产前沿面上，在所有DMU 中已经实现了产出和投入的最有效水平。在全要素生产率的研究框架下，以方向性距离函数为基础的碳生产率的表达式为：

(www.xing528.com)

如图3-1 所示，A 为决策单元的实际生产点，gx为投入的负向扩张，gy为产出的正向扩张，在两者的共同作用下，A 点沿着方向向量所指定的方向移动，从而达到B 点使得DUM 在确定的方向向量下实现有效产出和投入的最大同比例增减。

为了简化，将给定单元的投入向量x 确定为资本（K）、劳动（L）、二氧化碳排空间（C）3 个组成部分；产出向量为y。参照Kuosmanen（2005）的研究，放松模型产出与投入同比例增减的假设，令λj＝zj＋uj，那么全要素生产率研究框架下的碳生产率可以通过基于方向性距离函数的VRS（规模报酬可变）下的线性规划模型求得，即

图3-1　实现产出和投入最大同比例增减的方向性距离函数

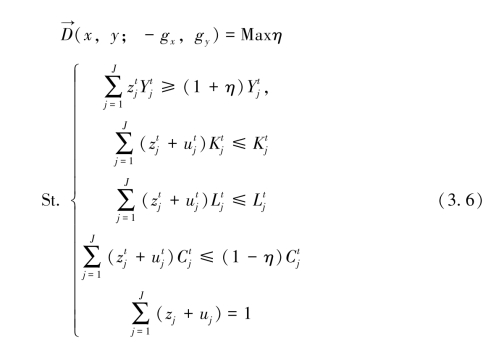
公式（3.6）中K 代表资本投入，L 代表劳动投入，C 代表二氧化碳排放空间的投入，Y 表示工业部门的经济绩效。根据上述模型，本书可测度出经济增长条件下满足减排要求的碳排放技术效率。η 代表二氧化碳排放空间利用的无效水平，maxη 反映的是在不增加任何其他投入（K、L）的情况下，给定单元二氧化碳排放减少和产出增长的最大提升空间。maxη 值越小说明给定单元二氧化碳排放空间投入和产出水平越接近生产前沿面，减排和增产潜力越小，效率越高。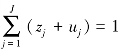，表明该模型是基于VRS 的模型，这是因为与CRS（规模报酬不变）相比，VRS 更接近于现实情形（Beede，et al.，1993）。

因此，基于方向性距离函数的Malmquist 碳生产率指数可以表示为：

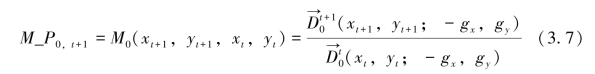
式中，（xt＋1，yt＋1）和（xt，yt）分别表示（t＋1）时期和t 时期的投入产出向量；和分别表示以t 时期技术T 为参照，时期t 和时期（t＋1）的方向性距离函数。