采用AHP法确定指标权重值。层次分析法可以将分析过程条理化、层次化,科学的简化分析过程,进而帮助决策选择。况且每个评估因素的重要性或权重对于整个体系而言又是不一样的,不能将每一个要素的权重视为等同,而层次分析法的优点在于将定性和定量相结合,强调系统化和层次化,确定的权重值具有科学性。
1.构造判断矩阵
权重值是指某项影响因素在对目标层进行分析中所占的比重。权重值的准确性直接影响着研究的科学性和结果的准确性。当前大多研究在计算因子权重值时,一般是依据评估者的经验和主观判断直接确定各项因子的权重,主观随意性较大,缺乏一定的客观性。本研究根据相对重要性比较标度表和层次结构模型图设计调查问卷。共选取了16名评估专家,收回有效调查问卷16份。再运用求矩阵特征值和特征向量的方法确定各项评估因子的权重。
层次指标两两比较结果是美国学者Satty等人提出的一致矩阵法,提出1-9标度法,该方法采用1、3、5、7、9及其倒数来确定标定标准,2、4、6、8表示上述相邻判断的中间值。这种方法不把所有要素放在一起比较,而是两两相互比较。对比时采用相对尺度,以尽可能减少性质不同要素相互比较的困难,以提高准确度。
表9.2 相对重要性比较标度表

本研究邀请专家对各因子之间的重要程度进行打分,根据有效问卷结果进行分析。对调查问卷的数据进行算术平均处理,然后对每一个比较因子赋值,构造相对重要性判断矩阵,用求矩阵特征向量的方法来确定权重值。由于评价指标比较多,本研究不逐一列出所有判断矩阵。
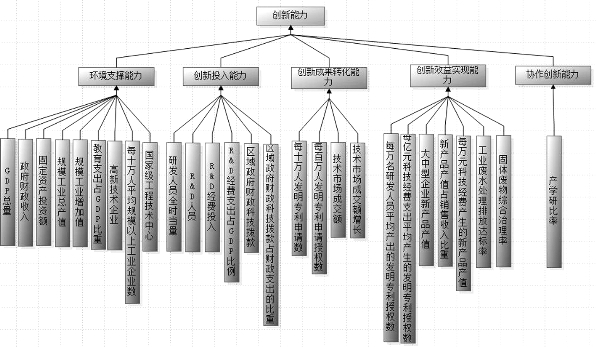
图9.2 科技城创新能力评价层次结构模型
2.计算权重
根据收回的16份问卷调查结果,对数据进行算数平均处理后,先对准则层的指标重要性赋值,再对27个评估因子的重要性赋值构建判断矩阵。
表9.3 构造判断矩阵

根据判断矩阵的结果,用方根法计算各指标权值:计算判断矩阵的每一行各元素乘积的n次方根,用其除以矩阵B行元素乘积的n次方根和,进行归一化处理,可得特征权向量(详见表9.4—9.9)。其中创新合作能力用关键指标产学研比率评价,因此权值为1,表省略。得出权值后,进行一致性检验,得出λmax=5.0734,CR=0.0164<0.1,符合一致性要求。
表9.4 目标层判断矩阵及中间层要素权重值
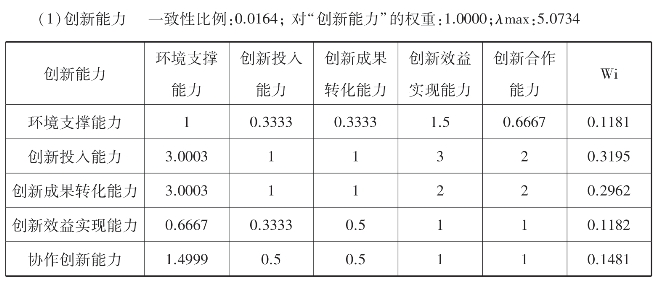
表9.5 环境支撑能力判断矩阵及因子权重值(https://www.xing528.com)

续表9.5
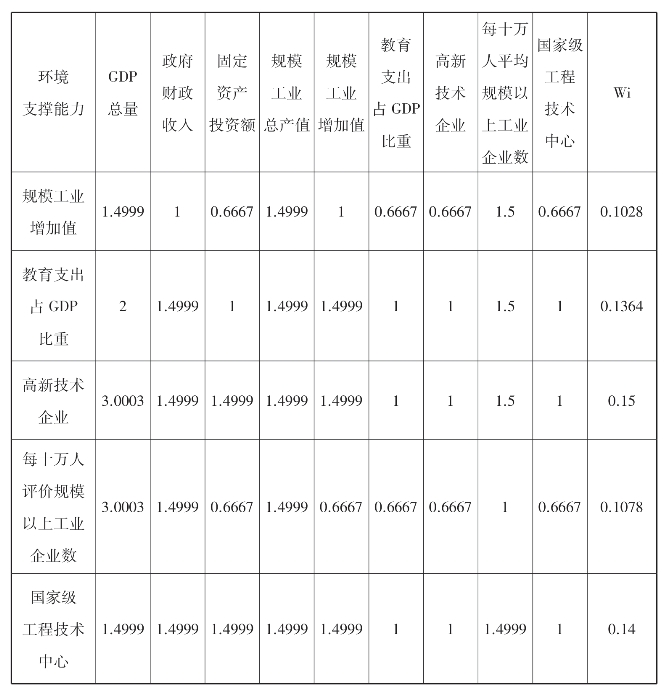
表9.6 创新投入能力判断矩阵及因子权重值
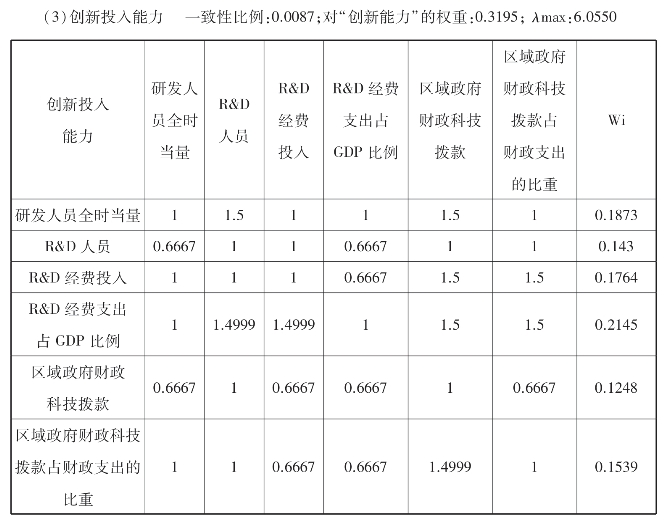
表9.7 创新成果转化能力判断矩阵及因子权重值
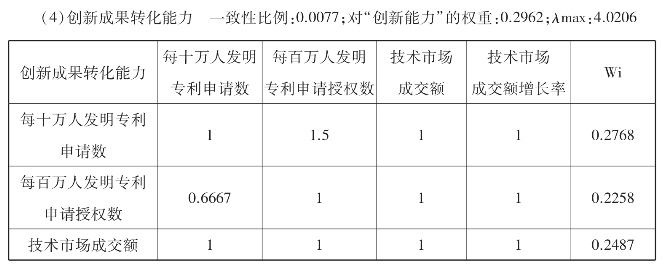
续表9.7
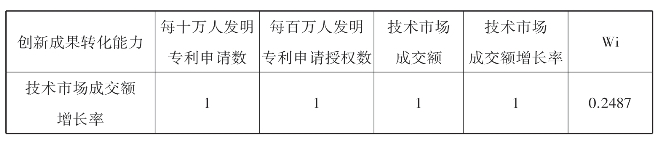
表9.8 创新效益实现能力判断矩阵及因子权重值

续表9.8

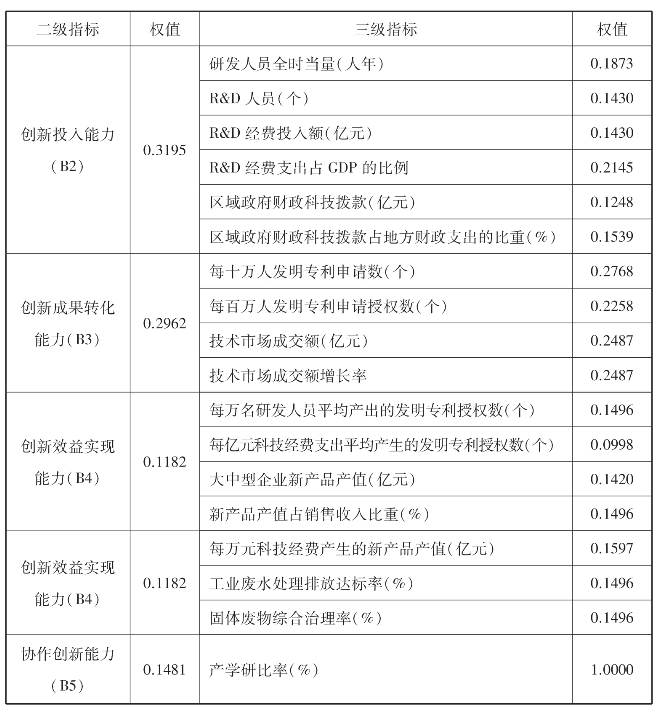
表9.9 评价指标权值一览表

续表9.9
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




