用投影理论评价非物资供应商的模型

p个决策评审专家对潜在供应商Ai（i=1，2，…，m）按照建立的评价准则Cj（j=1，2，…，n）进行选择，λk为决策评审专家Dk（k=1，2，…，p）的权重。ωj为评价准则Cj的权重。B1=（rij）m×h1（i=1，2，…，h1）表示决策变量为实数型部分矩阵，B2=（rij）m×（h2-h1）（i=h1，h1+1…h2）表示决策变量为区间数部分矩阵，B3=（rij）m×（n-h2）（i=h2，h2+1，…，n）表示决策变量为模糊语言部分矩阵。B=B1∩B2∩B3，则第k位专家的决策矩阵为

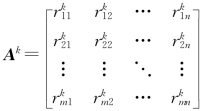
其中，rij中含有精确数类型数值、区间型数值以及语言数值。

投影可以很好地衡量两个项目之间的贴近程度，投影越大，两个项目之间越相近，因此可以借鉴投影理论去衡量供应商之间的相似程度，以此进行对比分析。

设向量α=（α1，α2，…，αn），向量β=（β1，β2，…，βn），则向量α与向量β 之间的夹角余弦值为

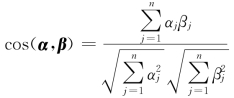
向量α=（α1，α2，…，αn），则向量α的模为

两向量之间的夹角余弦值可以衡量两个向量之间的方向，模可以衡量两个向量之间的大小，单独的一个均不能反映两个向量之间的相似程度，需要综合考虑两个向量的夹角余弦值和模的大小。

设向量α=（α1，α2，…，αn），向量β=（β1，β2，…，βn），则向量α在向量β上的投影为

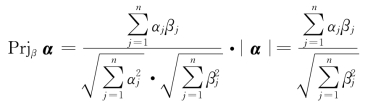
Prjβα 越大表示向量α 与向量β之间越相似，Prjβα 越小表示向量α 与向量β 之间相异程度越大。

1）属性值的规范化处理

为了解决不同量纲的数据不能对比的问题，将专家的评价值进行规范化处理。属性值包含效益型和成本型，其中订单完成率、订单准确率和信息共享属于效益型，价格属于成本型。

（1）属性值为实数的规范化

效益型规范化公式为

成本型规范化公式为

（2）属性值为区间数的规范化

效益型规范化公式为

成本型规范化公式为

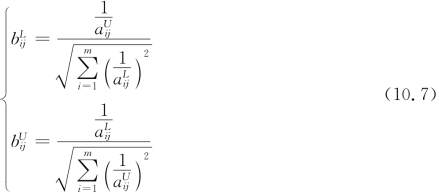
（3）属性值为模糊语言的规范化

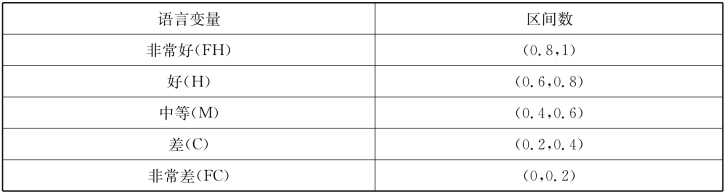
模糊语言集合主要有非常好、好、中等、差、非常差共5个等级，每个等级对应的区间数为x=（a，b），转化表如表10.2所示。

表10.2　模糊语言转化数据表

(www.xing528.com)

模糊语言转化为区间数后按照公式（10.4）和（10.5）进行规范化处理。

2）专家权重确定

在供应商选择的过程中，专家的权重往往是主观给出或者结合以往的经验给出。然而指标的评判本身就具有很大的主观性，权重的确定更加需要客观地给出。下面利用离差化思想求出专家的客观权重。

设第k位专家的判断矩阵为

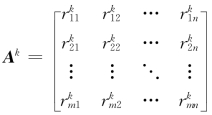
此矩阵中仅含有区间数和实数类型，模糊语言变量已转化为区间数形式。利用专家的评判矩阵Ak构造出差值矩阵Dk

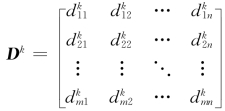
其中，dkij=|blkij-bluij|，blkij为区间的左端点，bluij为区间的右端点。当dkij为实数时其差值为0。进一步计算其总差值为

dk反映了第k 位专家的方案与其他专家方案的差距程度，dk越小，则差距越小，其权重也就越大。因此将此式取倒数并归一化处理后得到专家的客观权重为

3）个人评价信息集结

设F（a1，a2，…，an）=ωjbj，ωj是与函数F相关联的加权向量，ωj=1，这里称函数F 为n 维有序加权平均（OWA）算子。主要使用有序加权平均算子将个人评价信息集结成群体评价信息，即

4）计算综合优属度

投影算法主要研究两向量之间的相似程度，如果投影越大表示两向量之间越接近。针对含有实数、区间数的判断矩阵，下面采用投影算法进行方案的排序。

设X=（x1，x2，…，xh1）为所选取的理想方案，Y=（y1，y2，…，yh1）为所选取的负理想方案。其中X 从下界矩阵选取，当指标为效益性指标时，X=maxz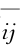；当指标为成本型指标时，X=minz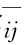。Y 从上界矩阵选取，当指标为效益性指标时，Y=minz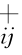；当指标为成本型指标时，Y=maxz。

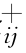计算下界矩阵在理想方案上的投影

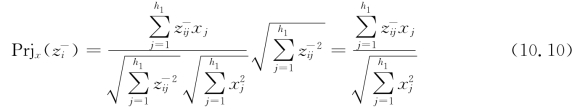
计算上界矩阵在负理想方案上的投影

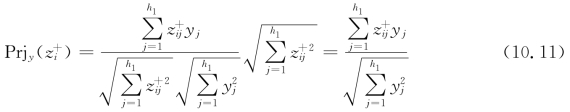
当方案Z的下界越接近理想方案时，则方案越优，即Prjx（z-i）越大越好。当方案Z 的上界越远离负理想方案时，则方案越优，即Prjy（z+i）越小越好。因此综合优属度需要考虑Prjx（z-i）和Prjy（z+i）的大小。假设方案Z隶属于理想方案的程度为φi，则隶属于负理想方案的程度为1-φi。建立如下函数

ξ（φi）=[φiPrjx（z-i）]2+[（1-φi）Prjy（z+i）]2，i=1，2，…，m

问题转化为求解模型maxξ（φi）。

令=0，解得

将φi 按照从大到小的顺序排序，即是方案的优劣排序。