在可变质量成本情形下,可以对非对称模型中工艺创新的影响进行详细分析。但在固定质量成本下,模型求解只能在对称条件下进行。本书用简化模型考察固定质量成本下的双寡头博弈,同样采用倒推归纳法,在产量阶段,求解一阶条件,则均衡产量为:
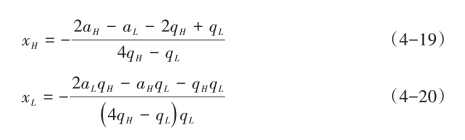
均衡利润为:
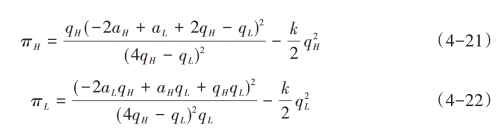
博弈的第二阶段,两企业同时选择各自的产品质量qH 和qL。在对称条件(aH = aL = a)下,首先证明,未采用工艺创新时博弈均衡的存在性和唯一性;再通过静态比较分析研究工艺创新的影响。
命题4.5 固定质量成本下,当ak ∈[0,0.00109]⋃[0.00218,0.01255]时,双寡头对称博弈(aH = aL = a)存在唯一均衡。
证明:为了证明均衡的存在性和唯一性,推导过程与命题1类似。
(1)对称情形aH = aL = a下,两企业利润关于质量的一阶条件为:
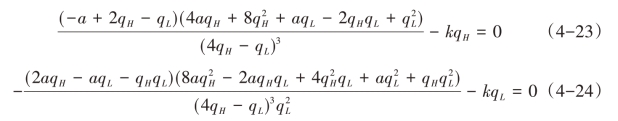
由于qH >qL,为方便求解,不妨加以转换qH = aq、qL = naq,其中n ∈[0,1]。则均衡产量变换为:
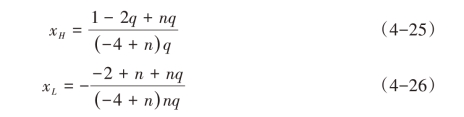
均衡利润变换为:
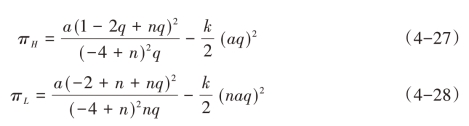
一阶条件变换为:
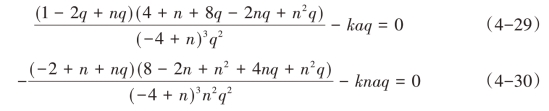
由式(4-29),令:
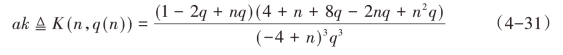
求解(4-29)(4-30),得关于q的两个根,分别为:
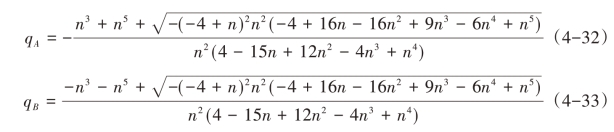
在式(4-32)和(4-33)中,根号下部分仅在n ∈[0,0.35834 ]上非负,而分母在n∈[0,0.35811 ]为正,在n∈[0.35811,0.35834 ]上为负。则qA >0的可行区间为n ∈[0.35811,0.35834 ],qB >0 的可行区间为n ∈[0,0.35834]。由于在区间n∈[0.35811,0.35834 ]上,均有πi(qA)>πi(qB),i=H,L。故n∈[0.35811,0.35834]时,q = qA;当n ∈[0,0.35811]时,q = qB。
(2)对称博弈下,均衡产量和均衡利润如式(4-25)—(4-28)所示。通过作图验证,当n ∈[0.35811,0.35834 ],q 取qA 时,均衡产量和均衡利润均为正。当q 取qB 时,均衡产量和企业H 的利润πH 为正,但仅在n ∈[0.32672,0.35811]上,有πL >0。如图4-5所示。
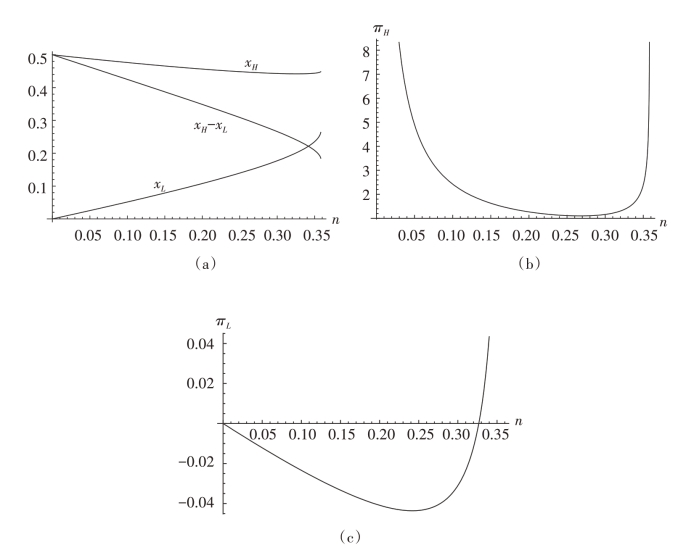
图4-5 q取qB时的均衡产量和均衡利润
(3)对称情形aH = aL = a 以及通过转换qH = aq 和qL = naq 后,二阶条件分别为:
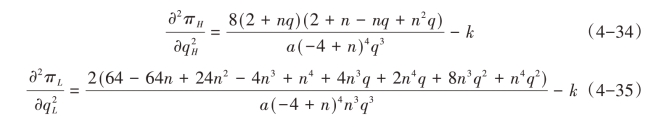
 (https://www.xing528.com)
(https://www.xing528.com)
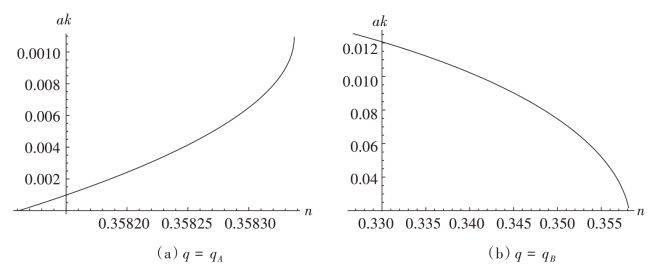
图4-6 q取不同根时的ak

综上,当ak ∈[0,0.00109 ]⋃[0.00218,0.01255 ]时,对称博弈存在唯一均衡。证毕。
与纵向差异化的文献相对应,本书的固定质量成本下双寡头博弈均衡中,两企业的产品质量存在差异化。由命题5 的证明过程可以发现,在区间 ak ∈[0,0.00109 ]上,双寡头博弈存在唯一纳什均衡; 而在ak ∈[0.00218,0.01255 ]上虽然存在两个纳什均衡,但对两个寡头企业而言均有πi(qA)>πi(qB),(i = H,L),则存在帕累托上策均衡。因此在区间ak ∈[0,0.00109 ]⋃[0.00218,0.01255 ]上,对称博弈存在唯一均衡。在博弈的第一阶段,考察两企业是否决定同时采用工艺创新以及创新对产品差异化有何影响。如前文所述,企业之所以采用工艺创新,往往是因为有利可图,有以下命题。
命题4.6 双寡头博弈(对称情形下)的均衡策略是在第一阶段同时采用工艺创新。
证明:
企业采用工艺创新往往意味着有利可图,由包络定理得:
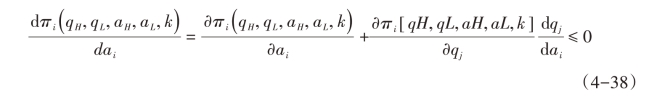
其中i,j = H,L;i ≠j。
企业H的利润πH关于aH和qL分别求导得:

综上,在ak ∈[0,0.00109 ]⋃[0.00218,0.01255 ]上,由于利润都将增加,两企业均有采用工艺创新的激励。证毕。
涉及固定质量成本,由于非对称情形求解过程的繁杂性,本书通过简化求解对称条件下的博弈均衡,命题4.6 具有重要的现实意义,即采用工艺创新使得边际生产成本降低对两企业而言均为占优策略。由命题4.5 的证明:在相应的参数区间上模型存在唯一解。双寡头博弈模型中,工艺创新通常存在两种驱动效应:一是工艺创新引发边际生产成本降低,促使企业将更多资本转向对产品研发的投入,为产品质量提升提供条件;二是企业采用工艺创新也旨在加大产品间的差异化,从而增加市场份额。对企业H 而言,两种效应方向相同促使其质量qH 提升;然而对于低质量企业L 而言,产品差异化水平的提高必然导致较低的质量qL。由于两种效应在不同的参数区间强度不同,产生不同的影响,得到命题4.7。
命题4.7 (a)若ak ∈[0,0.00109 ],均衡时工艺创新增加了企业H 的产品质量qH和产品间的差异化水平qH - qL,但降低了企业L的产品质量qL。
(b)若ak ∈[]0.00218,0.01255 ,均衡时工艺创新增加了两企业的质量qH 和qL,然而产品间的差异化水平qH - qL降低。
证明:随着工艺创新的采用,两企业的边际生产成本降低了,则均衡时产品质量和差异化水平随之发生变化。通过转换,则qH、qL 和qH - qL 在ak ∈[0,0.00109 ]和ak ∈[0.00218,0.01255 ]上分别如图4-7和4-8所示。
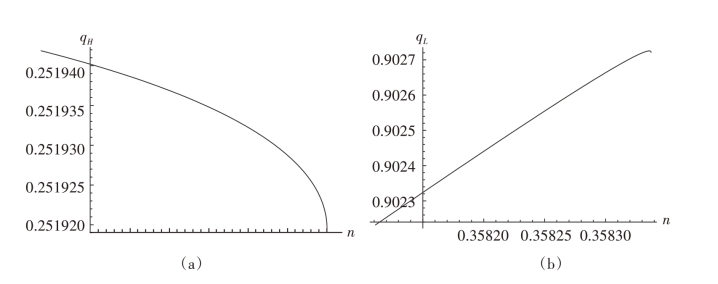
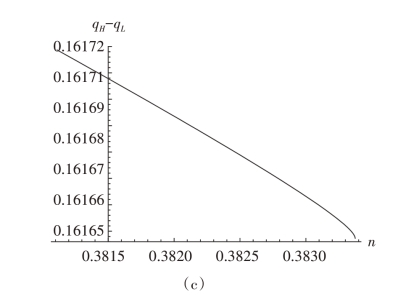
图4-7 q取qA时的均衡质量
由图4-6 (a) 知,当n ∈[0.35811,0.35834 ],ak 随n 单调递增。故在ak ∈[0,0.00109 ]上,均衡时工艺创新的采用提高了企业H 的质量,降低了企业L的质量,从而使得产品的差异化水平提高。
而由图4-6 (b) 知,当n ∈[0.32672,0.35811 ],ak 随n 单调递减。则在ak ∈[0.00218,0.01255 ]上,随着工艺创新的采用,两企业的质量都提高了,但产品的差异化水平却降低。证毕。
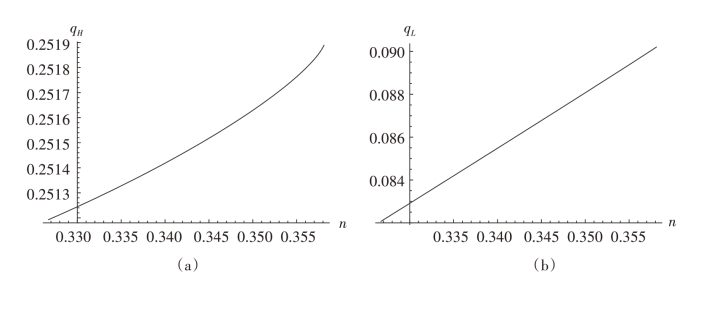
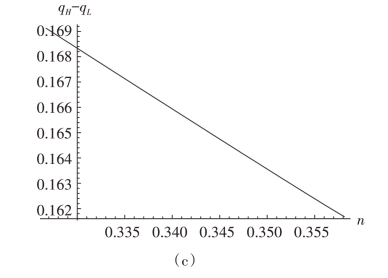
图4-8 q取qB时的均衡质量
命题4.7 的现实意义为,边际生产成本较低时,企业间的竞争较为激烈。工艺创新引入后,使得企业H提高产品质量,为弱化竞争必然采用差异化策略,而企业L 则只能降低产品质量。总之,对企业H 而言,工艺创新促进了产品创新;而对企业L而言,产品质量降低了。由于企业需通过工艺创新提高其工艺技术水平,进而满足更高质量产品的设计与制造的要求。因此,若将固定质量成本看作为获得更高质量所必需的研发投入,则产品创新与工艺创新存在互补关系。
而边际生产成本较高时,为了增加利润,企业势必提升产品质量。随着工艺创新引起相应边际生产成本的降低,两企业的产品质量都提高了,但差异化水平缩小。因此,对两企业而言,工艺创新引发了以质量提升为目的的产品创新。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




