博弈均衡分析：可变质量成本下的策略探究

可变质量成本下，给定两企业的利润函数，从产量决策阶段开始，采用倒推归纳法求解。首先分析未采用工艺创新时双寡头博弈均衡的存在性和唯一性；其次，进行比较静态分析，考察采用工艺创新所产生的影响。

分别求解利润函数（4-3）关于产量的一阶条件，得均衡产量：

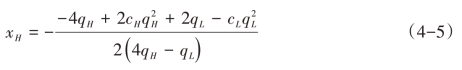
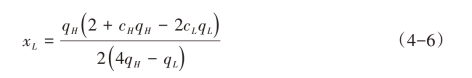
均衡利润为：

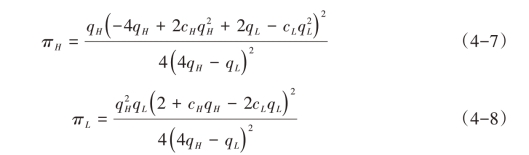
当博弈进行到第二阶段，两企业同时选择各自产品的最优质量。在相应的参数区间上，命题4.1证明了博弈均衡的存在性和唯一性。

命题4.1 当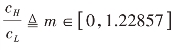时，双寡头博弈存在唯一均衡，两企业分别生产质量为qH和qL的差异化产品。

证明：为证明均衡的存在性和唯一性，首先关于企业利润最大化求解一阶条件；其次证明内部解并验证二阶条件；最后证明均衡的唯一性。

（1）为便于求解，进行简单转换，令cH = mc 和cL = c，其中m 和c 均为正。由于均衡产量xH ＞0和xL ＞0，则企业利润关于产品质量的一阶条件为：

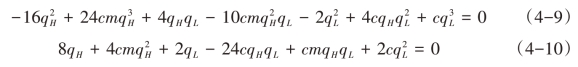
将式（4-13）和（4-14）带入利润函数（4-7）和（4-8）得：

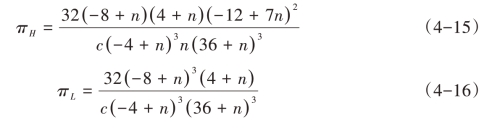
（2）m和q的图像如图4-1所示：

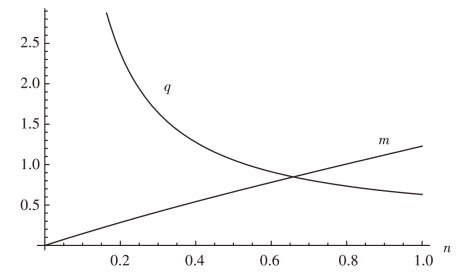
图4-1 博弈均衡时的m和q

在n ∈(0，1)上，m 单调递增且m ∈[0，1.22857]。m 在n ∈[0，0.99788]上是凹函数，在n ∈[0.99788，1]上是凸函数。而q在n ∈(0，1)上为正且单调递减。

均衡产量以及均衡利润在n ∈(0，1)的图像为：

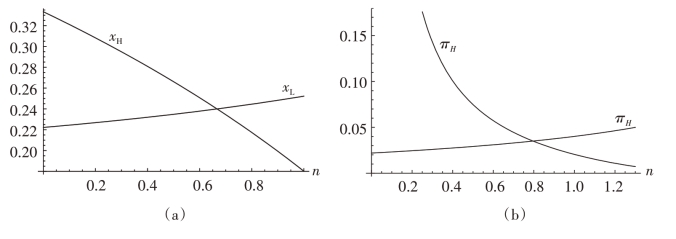
图4-2 均衡产量和均衡利润

由图4-1 知，在n ∈(0，1)上，m(n)单调递增且m ∈[0，1.22857]，而q(n)则单调递减。若外生给定m 的任意值都有唯一的n 与之对应，相应地有唯一的q( )

n 。

为便于考察，选取区间[0，1.22857]上m 的代表值，用相同的方法得到同样性质的结论（如表4-1 所示）。则对于任意的m ∈[0，1.22857]，在相应区间内二阶条件均满足，且存在最优质量和最大利润。(www.xing528.com)

由表4-1 可知： πH 随m 增大而减小，πL 正好相反； 且在m ∈[1.00302，1.22857]上，πL ＞πH，印证了图4-2的结论。综上，双寡头博弈均衡的存在性和唯一性得证。证毕。

表4-1 博弈均衡时企业的最优质量和最大利润

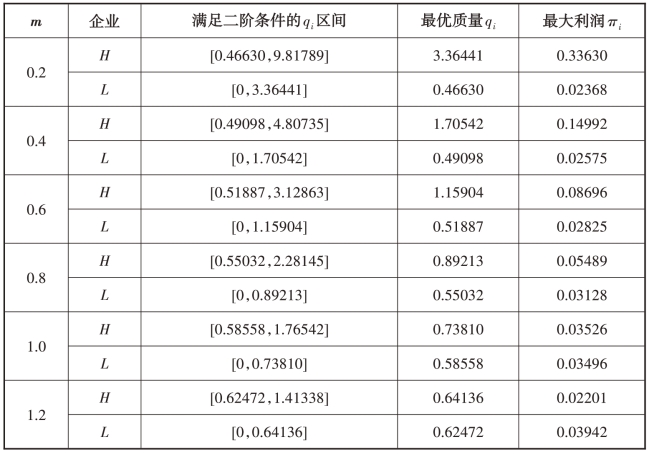
命题4.1 显示，在边际成本成比例的相关区间上，存在两寡头博弈的唯一纳什均衡，即给定竞争对手的质量和产量决策，每个企业都有最优策略可以选择。为便于求解而进行简化处理，即假设cH = mc和cL = c。其中m 用于衡量企业H 采用工艺创新的技术优势，即当m减小时，与对手相比企业H的技术优势增大。若m ＜1，企业H 比对手更具生产效率；而m ＞1时则相反。相比Battaggion 和Tedeschi（2006）基于Bertrand 竞争的分析，Cournot 竞争对双寡头企业，特别是低质量弱势企业的创新决策有着重要的指导意义。由命题4.1 的证明，企业L 在m ∈[1.00302，1.22857]上的利润大于对手，说明低质量企业在进行工艺创新后生产效率大幅提高从而降低了边际生产成本，增加了自身利润同时在市场竞争中更具优势。通过比较静态分析，得到命题4.2。

命题4.2 （a）若两寡头企业的边际成本等比例下降（即c 降低），则均衡时产品质量qH、qH以及质量差距qH - qL都增大。

（b）若企业H 技术优势增加（即m 降低），则均衡时产品质量qH 及质量差距qH - qL均增大，而企业L的产品质量qL减小。

证明：

（a）由式（4-11）（4-12）知：一阶条件并不依赖于c，故方程组的解m 和q也与c无关。则均衡时qH、qL和qH - qL都随c的增大而减小。

（b）均衡质量qH和qL以及质量差距qH - qL如图4-3所示。

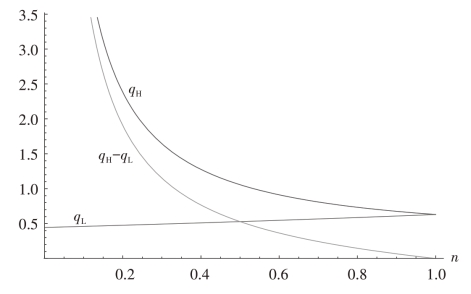
图4-3 博弈均衡时的产品质量与差异化水平

则qH 和qH - qL 随n 的增大而减小，而qL 随n 的增大而增大。由于m 随n 单调递增，故随高质量企业技术优势的增大，则均衡时qH 增大，qL 减小，质量差距qH - qL增大。证毕。

在第一阶段，企业需做出决策是否采用工艺创新。为衡量工艺创新对产品纵向差异化的影响，常用边际生产成本的降低（即ci的减小）表示工艺创新。现实中，企业必然有利可图才采用工艺创新，因此需确认采用工艺创新后两企业的利润变化情况，有以下命题。

命题4.3 两企业都有采用工艺创新的激励，且同时采用工艺创新是子博弈的均衡策略。

证明：两企业的均衡利润如式（4-15）和（4-16）所示。为便于考察特定企业关于工艺创新的采用决策，假定对手企业未采用创新，即对手企业的边际生产成本保持不变。

在低质量企业L 尚未采用工艺创新时，其边际生产成本维持在cL（即保持c不变）。高质量企业H 采用工艺创新等价于其边际生产成本cH 的降低（即m 的减小）。由图4-2（b）知，均衡利润πH 随m 的减小而增大，故倾向于采用工艺创新。

而高质量企业H尚未采用工艺创新时，其边际生产成本维持在cH（即保持mc不变）。低质量企业L的工艺创新等价于其边际生产成本cL的降低（即c的减小），均衡利润为：

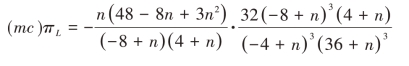
由图4-4 可知，低质量企业的利润πL 随m 的增大而增大。但由于保持mc 不变，故πL 随c 的减小而增大，则低质量企业同样有采用工艺创新的激励。综上，对高低质量企业而言，工艺创新均有利可图，因此都有采用创新的激励。采用工艺创新均为占优策略，故两企业同时采用。证毕。

图4-4 企业L的工艺创新激励

在比较静态分析中，命题4.3 考察了工艺创新的两种不同方向：等比例工艺创新和非比例工艺创新。通常保持两企业的边际成本比例不变，等比例工艺创新意味着参数c 的减小。非比例工艺创新指：企业L 的边际生产成本保持不变，仅企业H 的技术优势增加，即给定c 时，非比例工艺创新意味着参数m 的减小。本书研究工艺创新对产品创新的影响，重点考察的是采用工艺创新后，企业利润以及产品质量的变化。通过与未采用工艺创新时结论的比较分析，无论等比例抑或非比例工艺创新都将增加利润，双寡头企业都有采用激励。但针对低质量弱势企业的工艺创新，以上命题具有重要的现实意义。企业L唯有更大程度降低边际成本，通过提高生产效率扩大自身优势以拉开技术差距，从而占据更多市场份额实现利润最大化。由命题2 的结论以及对两种创新的定义，得到以下命题。

命题4.4 （a）等比例工艺创新增加了均衡时企业的产品质量qH 和qL 以及差异化水平qH - qL。

（b）由企业H的相对技术优势所体现的非比例工艺创新，增加了均衡时企业H的产品质量qH和差异化水平qH - qL，然而降低了企业L的产品质量qL。

通过等比例工艺创新，两企业的边际成本成比例降低，其经济解释为：等比例工艺创新均降低了边际成本，使得企业间的产量竞争趋于激烈，从而引发企业间产品差异化水平的提高。基于差异化和利润的考虑，企业H借助工艺创新提升产品质量。对企业L而言，工艺创新使边际成本降低，有利于提升产品质量，但产品差异化策略又促使其降低质量，需要在两者间权衡。企业L因前一种效应较强而提高其产品质量，且由于企业H的产品质量有较大幅度的提升，两者的差异化水平仍增大。

非比例工艺创新主要体现了企业H相对于竞争对手的技术优势。工艺创新使边际成本降低，提升了企业H的技术优势，从而生产更高质量的产品，增大产品间的差异化，缓和企业间的激烈竞争。对企业L而言，一方面，同样基于差异化的考虑，趋于降低产品质量；另一方面，如果企业H 的非对称技术优势充分大，企业L 也可能提高质量。事实上，若企业间产品差异化水平较低，即使企业H 拥有技术优势且质量较小幅度提升，企业L也只可能降低产品质量。