技术差距的界定与模型设定方法

考虑产品纵向差异化市场上高低质量企业垄断竞争的标准模型。假定消费者的偏好程度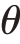 均匀分布在[0，1]上，每个消费者只购买两种纵向差异化产品的一种或者不购买任何产品，则偏好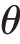的消费者以价格p购买质量q的产品，获得的效用为U = 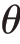q - p。

假定市场只有两个企业，分别只生产同种新产品的高低两种质量类型的一种，即高质量企业H 只生产高质量qH 型新产品，低质量企业L只生产低质量qL型新产品，其中qH ＞qL。关于成本函数，本书采用Zhou（2002）、Jinji和Toshimitsu（2004）的设定，假设固定质量成本非对称，即企业间可能存在较大技术差距，这样的改进更符合实际情况^[1]。技术差距可以解释为：同样为了获得质量q 的新产品，两企业的研发成本不同，拥有技术优势的高质量企业H投入C(q)即可，而技术劣势的低质量企业L 则需投入更多的γC(q)才能获得质量q，其中γ ＞1。关于边际生产成本，为简化模型，本书假定为零。采用Ronnen（1991）的假设形式，固定质量成本函数C(q)有以下特性：C(0) = C′(0) = 0；对任意的q ＞0 有C′(q )＞0 和C′′(q) ＞0；。本书假定固定质量成本为二次函数形式，即。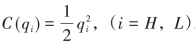

假设向高质量企业H 和低质量企业L 购买产品无差异的消费者的偏好程度为HL，购买低质量企业L 的产品和不购买任何产品无差异的消费者的偏好程度为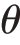L0，则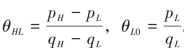。本书为比较Bertrand和Cournot两种竞争类型下两寡头企业的策略选择，故假定市场未完全覆盖，即存在部分消费者不购买任何产品。则在未完全覆盖市场中，高质量企业H 和低质量企业L 所面临的需求函数分别为：

根据需求函数和假定的固定质量成本函数，双寡头企业的利润函数为：(www.xing528.com)

其中Ri = pidi表示两企业的收益函数，i = H，L。

本书设定一个两阶段博弈的纵向差异化模型，分析两企业如何在Bertrand 竞争和Cournot 竞争下，选择其创新产品的质量以及均衡价格和均衡数量，同时分析两种竞争类型下，消费者剩余和社会福利等随企业间技术差距的变化情况。在第一阶段，两企业同时选择各自将生产的产品质量qH和qL。第二阶段，两企业进行Bertrand竞争以决定产品的价格，或进行Cournot竞争以决定产品的产量。本书以逆向求解方法来推导子博弈完美均衡。