低质量企业领导问题探讨

当领导企业1 生产低质量qL 产品，而跟随企业2 则以高质量qH( ＞qL)产品后进入市场时，两企业的累积贴现利润及市场均衡将发生改变。因此，低质量企业领导下，两企业的累积贴现利润分别为：

两企业通过最大化各自的跨期贴现利润而进行质量决策，有以下命题。

命题2.2 当领导企业以低质量产品率先进入市场时，存在3种均衡：

（1） 若两企业产品的差异化水平x ∈[1.03680，1.14039]，则均衡利润π1L ＞0、π2H ＜0，跟随企业在t2时不进入市场，领导企业永久保持垄断优势；

（2）若两企业产品的差异化水平x ∈[1.14039，1.68527]，则均衡利润均为正，且π1L ＞π2H，在t ∈[t2，∞)上形成双寡头垄断竞争市场；

（3）若两企业产品的差异化水平x ∈[1.68527，2.79243]，则均衡利润均为正，但π1L ＜π2H，在t ∈[t2，∞)上形成双寡头垄断竞争市场。

证明：

令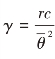，，则式（2-20）和（2-21）转变为：(www.xing528.com)

同样，令qL = q、qH = xq，则两企业的贴现利润关于各自质量的一阶条件简化为：

联立求解得：

则满足0 ＜μ(x) ≤1 的x 可行区间为[1.03680，2.79243]，且在此区间上μ(x)单调递增，μ(1.03680) = 0 和μ(2.79243) = 1。二阶条件均满足，即 和。因此，当且仅当x ∈[1.03680，2.79243]时，μ(x)才有意义。

领导企业1的跨期贴现利润为：

在[1.03680，2.79243]上单调递减且有正利润，即π1H ＞0。而跟随企业2的贴现利润为：

在[1.03680，2.79243]上单调递增，但当x = 1.14039 时，。故当x ∈[1.03680，1.14039]时，π2H ＜0；而x ∈[1.14039，2.79243]时，π2H ＞0。

通过比较式（2-28）和（2-29）发现，当x ∈[1.03680，1.68527]时π1L ＞π2H，而x ∈[1.68527，2.79243]时π1L ＜π2H。因此，得到：当x ∈[1.03680，1.14039]，π1L ＞0，π2H ＜0；x ∈[1.14039，1.68527]，π1L ＞π2H ＞0；x ∈[1.68527，2.79243]，π2H ＞π1L ＞0。证毕。