如何利用DEA模型进行相对效率评价

数据包络分析法（Data Envelopment Analysis，DEA）是一种衡量多种投入和多种产出决策单元（Decision Making Unit，DMU）相对效率的综合评价方法，主要用于评价相同种类单元间的相对效率性。数据包络分析法（DEA）最初由Charnes、Cooper和Rhodes在1978年提出，他们提出的就是著名的CCR模型，这种通过构建生产前沿面对决策单元的相对效率进行评价的方法得到了广泛的使用，后来在此基础上又得到了很大的发展。^[2]利用数据包络分析法（DEA）分析，有如下的优点：首先，它可以对一个具有多投入、多产出的决策单元的生产（或经营）效率进行评估。由于DEA并不需要特定的投入与产出的生产函数形式，因此它可以用于具有比较复杂的决策单元的生产（或经营）效率的评价。其次，它还具备单位不变性的特点，即DEA衡量的DMU的效率不会受到投入与产出数据中单位的影响。再次，DEA模型的投入与产出变量的权重是由数学规划根据数据生成的，无需预先设定投入和产出的权重，这样就避免了人为主观判断的影响。最后，DEA还可以进行差异分析、效率分析和敏感性分析，可以进一步了解决策单元中资源利用的状况，为企业管理者的生产与经营决策提供重要参考。^[3]

本章首先介绍最早被广泛使用的以投入为导向的CCR模型。

（一）CCR模型

CCR模型^[4]是由Charnes、Cooper和Rhodes提出的一个以投入为导向并且假定规模报酬不变的DEA模型。具体数学模型如下：

假设有n组决策单元DMU，其中每个单元都有m种投入和s种产出，则其决策变量的效率值为：

其中，h0为目标决策变量的相对效率值，xij表示了第j个决策单元对第i种输入的投入量，yrj表示了第j个决策单元对第r种输出的产出量，ur，vi均为权变量，且大于等于0，并且能够通过上述模型求出其合适的权重。

但是上述模型并非线性规划模型，所以会有无穷多解。为了避免这种情形的发生，我们得出如下的一般形式（以投入为导向的CCR模型）：

其中，x0表示决策单元的投入量，而y0表示决策单元的产出量。θ是总技术效率值（TE），λj为各决策单元的权重乘数；s+，s-为松弛变量。松弛变量表征的是实际观测值和效率最优值的差值。

假定s-0，s+0，θ0为该规划的最优解，可以得出如下结论：

第一，若θ0=1，s-0，s+0至少有一个大于0的，则称该决策单元是弱DEA有效，且该决策单元不是同时技术有效和规模有效。

第二，若θ0=1，并且s-0=0，s+0=0，则该决策单元是DEA总技术有效的。并且，此时决策单元同时为技术有效和规模有效。

第三，若θ0<1，则该决策单元为DEA无效。

同理，以产出为导向的CCR模型的具体形式如下：

以产出为导向的CCR模型与以投入为导向的CCR模型原理相同，只是考察效率的角度不同。以投入为导向的CCR模型是在产出固定的情形下，通过比较特定的决策单元的投入和生产前沿面上的投入，确定该决策单元的效率值。而产出导向的CCR模型则是在投入固定的情形下，通过比较特定的决策单元的产出和生产前沿面上的产出，确定该决策单元的效率值。

（二）BCC模型

CCR模型衡量的技术效率是规模报酬不变假设下的相对效率，但事实上并不是每一个DMU都是在规模报酬不变的情况下生产的，DMU可能是在规模报酬递增或规模报酬递减的情形下。DMU的无效率，除了因为其自身在投入和产出的资源配置不合理以外，或许也是由自身的规模不当引起的。因此，Banker、Charnes和Cooper于1984年将CCR模型改进为BCC模型^[5]，即在CCR模型上增加假设条件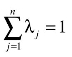，其为一个凸型假设。而BCC假设又称为VRS（规模报酬可变）模型，该模型去掉了规模报酬不变这个限制条件，并使得技术效率等于纯技术效率乘以规模效率。利用该BCC模型，可以求出各DMU的技术效率（VRSTE）、纯技术效率（PTE）和规模效率（SCALE），而且技术效率=规模效率×纯技术效率，（即VRSTE=PTE×SCALE）。

在规模报酬可变模型的假设条件下，投入导向的BCC模型如下所示：

同样，假定s-0，s+0，θ0为该规划的最优解，则我们可以得出下面的结论：

第一，BCC模型比CCR模型多出了一个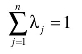约束条件，所以若θ0=1，并且s-0=0，s+0=0时，则决策单元DMU为纯技术效率有效，否则就为纯技术效率非有效；

第二，若θ0=1，则规模报酬不变；

第三，若θ0>1，并且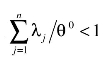，则规模报酬递增；

第四，若θ0<1，并且，则规模报酬递减。

同样，我们可以得出以产出为导向的BCC模型，具体模型形式如下：

（三）DEAP 2.1软件介绍

在分析DEA模型时，经常需要借助相关软件进行计算，本章使用DEAP 2.1软件进行数据处理。下面简单介绍一下该软件的使用过程以及重要参数。

第一步，首先设置参数、变量及选定所用模型。打开文件123.ins即可看到如下参数：

123.dta　　DATA FILE NAME

123.out　　OUTPUT FILE NAME(www.xing528.com)

213　　　　NUMBER OF FIRMS

8　　　　　NUMBER OF TIME PERIODS

2　　　　　NUMBER OF OUTPUTS

3　　　　　NUMBER OF INPUTS

0　　　　　0=INPUT AND 1=OUTPUT ORIENTATED

1　　　　　0=CRS AND 1=VRS

0　　　　　0=DEA(MULTI-STAGE),1=COST-DEA,

2=MALMQUIST-DEA,3=DEA(1-STAGE),4=DEA(2-STAGE)

第一行123.dta表示将要分析运行的文档名称。

第二行123.out为软件运行后输出的结果。

第三行表示决策单元数量，本章一共选取了213个决策单元。

第四行表示时期数，我们选取的是从2005年至2012年的数据，所以时期数为8。

第五行表示产出数，本章一共有两个产出变量，所以产出数为2。

第六行表示投入数，本章一共有三个投入变量，所以投入数为3。

第七行表示是以投入为导向或以产出为导向衡量技术效率，我们选取的是以投入为导向，所以参数为0。

第八行表示规模报酬，0表示CCR模型，1表示BCC模型。因为我们选取的是BCC模型，所以模型数为1。

第九行是内部计算方法，在本章中选0即可。

第二步，从123.out中输出结果，对其中部分参数的解释如下：

输出的数据一共为四列，而这四列数据分别表示：

firm 样本次序；

crste 不考虑规模收益的情况下的技术效率（综合技术效率）；

vrste 考虑规模收益的情况下的技术效率（纯技术效率）；

scale 考虑规模收益的情况下的规模效率（规模效率）。

纯技术效率和规模效率是对综合效率的细分。

最后一列irs，---，drs分别代表规模收益的递增、不变和递减。

第三步，针对各结果，进行整理、分析和评价。