期权价值和定价模型：实物期权解析

1.期权价值及其影响因素

期权的总价值是由期权的“内在价值”和“时间价值”两部分构成的。其中，内在价值是期权的执行价格与资产的市价之差。实值期权的内在价值等于ST减去X（ST表示标的资产到期日的市场价格，X表示执行价格），虚值期权和两平期权的内在价值为零。时间价值是期权应具有的超出基本的内在价值的价值。期权的大部分时间价值是一种“波动性”价值，依赖于当执行对自己不利时可以不执行的权利。当资产市价与执行价格相等时，期权的时间价值最大，而无论资产价格向哪个方向变动，这种超额的时间价值都将下降。

期权的价值受六个因素的影响：期权的执行价格、期权的到期日、标的资产当前价值、期权有效期内的无风险利率、标的资产价值变化的方差和标的资产支付的红利。其中，标的资产当前价值、标的资产价值变化的方差及标的资产支付的红利是与标的资产相关的因素，期权的执行价格和期权的到期日是与期权合约有关的因素，而期权有效期内的无风险利率是与金融市场相关的因素。

（1）标的资产当前价值。期权是一种取决于标的资产价值的资产。由于买入期权提供了以固定价格购买标的资产的权利，因此，标的资产当前价值的上升使买入期权的价值增加。卖出期权则相反，随着标的资产当前价值的上升，期权的价值将减少。

（2）标的资产价值变化的方差。方差越大，说明标的资产价格波动越大。标的资产价格变化的幅度越大，期权的价值越高。这一点对于买入期权和卖出期权都是一致的。

（3）标的资产支付的红利。期权有效期内，如果标的资产支付红利（如股利），则买入期权的价值是预期红利支付额的递减函数，而卖出期权的价值则是预期红利支付额的递增函数。

（4）期权的执行价格。对于买入期权，期权的价值随着执行价格的上升而减少。而对于卖出期权，期权的价值随着执行价格的上升而上升。

（5）期权的到期日。随着距离期权到期日时间的增加，买入期权和卖出期权都会变得更有价值。距离到期日的时间越长，标的资产价值可以变动的时间越长，两类期权的价值就都会上涨。

（6）期权有效期内的无风险利率。期权费的机会成本取决于利率水平和距离期权到期日的时间。期权的购买者仅在执行期权时才支付执行价格，延迟支付在利率高（低）时具有较大（小）价值。因此，利率的升高将使买入期权的价值增大，使卖出期权的价值减小。

2.实物期权的定价模型

实物期权的基本定价模型可以分为以下两类：

（1）连续时间状态下的Black-Scholes（布莱克-斯科尔斯）期权定价模型。这是美国芝加哥大学教授费希尔·布莱克（Fischer Black）与斯坦福大学教授迈伦·斯科尔斯（Myron S.Scholes）在1973年提出的期权定价模型，该模型又被称为连续的二叉树模型。其公式如下：

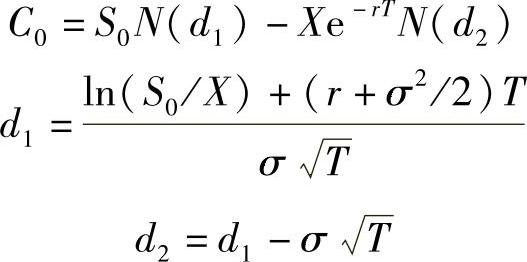
式中，C₀为当前的买入期权的价格；S₀为当前的资产价格；N（d₁）为标准正态分布小于d的概率；X为执行价格；e为自然对数的底，等于2.71828；r为无风险利率；T为期权到期时间；σ为资产连续复利的年收益率的标准差。(www.xing528.com)

（2）二叉树定价模型。二叉树定价模型的基本思想是：假设标的资产的价格运动是时间离散的，把期权的有效期分为若干个足够小的时间间隔，在每一个非常小的时间间隔内假定标的资产价格从开始的S运动到两个新值。当前标的资产价格为S，期权价格为f。假设期权有效期为T，在期权有效期内标的资产价格或者从S向上变动到一个新水平S_u（u＞1，d＜1），运动到比现价高的值S_u的概率为P，或者从S向下变动到一个新水平S_d（0＜d＜1），运动到比现价低的值S_d的概率为1-P。如果标的资产价格上升到S_u，假设期权收益为C_u；如果标的资产价格下降到S_d，假设期权收益为C_d。

在下一个时间段里，标的资产的可能价值为S_uu、S_ud、S_dd，以此类推。单步和两步二叉树图中的标的资产价格如图16-1所示。

假设资产的现价为S，执行价格为X，有效期为一期，无风险年利率为r，则到期后期权可能的价值为C_u=max（0，S_u-X）、C_d=max（0，S_d-X），假设一个组合由Δ份的标的资产多头头寸和一个看涨期权的空头头寸构成，投资组合的到期价值分别为S_uΔ-C_u、S_dΔ-C_d，则S_uΔ-C_u=S_dΔ-C_d。

图16-1 单步和两步二叉树图中的标的资产价格

期权的价值为：

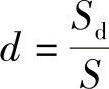令，表示资产价格上升后是原来价格的倍数；，表示资产价格下降后是原来价格的倍数，且0＜d＜1，u＞1。

整理得到一期期权的价值为：

推而广之，根据时期为一期的期权价值的二叉树模型，可以采用由后向前推进的方法计算两期甚至多期期权的价值，如两期二叉树模型为：

C=e^-2rT[p²C_uu+2p（1-p）C_ud-（1-p）2C_dd]

式中，C_uu=max（0，S_uu-X），C_ud=max（0，S_ud-X），C_dd=max（0，S_dd-X）；e^-2rT为第二期期末的价值的折现率。