不确定型决策方法详解

1.不确定型决策的特征与评价

不确定型决策又称非确定型决策，是指决策者在决策时，不知道所处理的未来事件在各种特定条件下的明确结果（自然状态），以及各种结果发生的概率，决策者在一种无法肯定的情况下进行的决策。例如，某住宅投资项目随着市场状况的不同会有不同的销售额，从而盈利也不同。但是市场是繁荣、萧条还是平稳，其概率并不清楚。投资者在这种情况下进行的决策就是不确定型决策。

作为不确定型决策，一般应具备以下特征：①有一个（组）明确的决策目标；②有两个以上可供选择的方案；③实现方案的未来状态有两个或两个以上；④不同方案在不同未来状态下的预期结果可以估算出来。

不确定型决策问题与风险型决策问题的主要区别在于它不知道各个自然状态出现的概率。风险型决策虽然也具有不确定性，但它可以预先估计出各个自然状态出现的概率。

由于决策者对未来可能发生的变化不能作出预期决定，因此，不确定型决策的决策结果在很大程度上依赖于决策者对风险所持的态度。因为信息不全，决策者的决策有较大的主观随意性。

2.不确定型决策的方法

不确定型决策的方法有以下五种：

（1）小中取大法。该方法又称最大最小决策法，或称最大最小决策准则，是一种悲观、保守的决策方法。这种方法的目的是把决策风险降低到最低程度，把安全放在首要的位置来对待。决策时，决策者总是考虑每个方案中最悲观的结果，并在所有最悲观、最坏可能的结果中选择亏损最少、收益值最大的方案作为最合理的决策方案。

小中取大法决策的步骤是：①确定几个备选方案；②从每一备选方案中选择一个最小的报酬率（收益值）；③从上述最小的报酬率（收益值）项中，选择一个报酬率（收益值）最大的方案作为决策方案。

（2）大中取大法。该方法又称乐观准则，即决策者对未来市场客观规律总是抱乐观态度，按照这种方法进行决策，通常都是选取方案中不同状态下估计损益值最大值中的最大值。采用这种方法的决策者属于风险喜好型，往往敢于冒风险，极力追求最大投资利益。

（3）乐观系数法。乐观系数法又称折中决策法，其特点是，对客观条件估计既不那么乐观，也不那么悲观，而是用系数平衡一下，表示乐观程度的系数则称为乐观系数。

利用乐观系数法进行决策的步骤是：①决策者根据掌握的资料和已积累的经验，确定一个乐观系数α，α值的大小表示对问题的乐观程度。α=1时，为最乐观情况；α=0时，为最悲观情况。通常，α的范围是[0，1]。②求取各方案的损益值。方案的损益值等于α乘以最乐观的损益值，再加上（1-α）乘以最悲观的损益值的和。③比较各方案的损益值，选择支出最小或收益最大的方案为最优决策方案。

（4）最小后悔法。该方法也称后悔值决策法。决策者在制定决策后，若事实不符合理想状态，他就可能会对他选择的方案后悔，希望自己以前选择的方案是完全不同的方案。该方法的实质是后悔最小的方案为最合理的方案。用这个方法决策，首先要求出每个方案在各种自然状态下的后悔值——最高值与其他值之差；然后，比较各方案的最大后悔值，从这些最大后悔值中选择最小的一个，其对应的方案就是最优的方案。

（5）机会均等法。机会均等法又称同等概率法。决策者在决策过程中，不能肯定各种自然状态出现的概率，就简单地认为它们出现的概率是相等的。如果有n个自然状态，则每个自然状态出现的概率为1/n。然后按照风险型决策方法，计算各方案的利润期望值，选取期望值中最大者为最优方案。

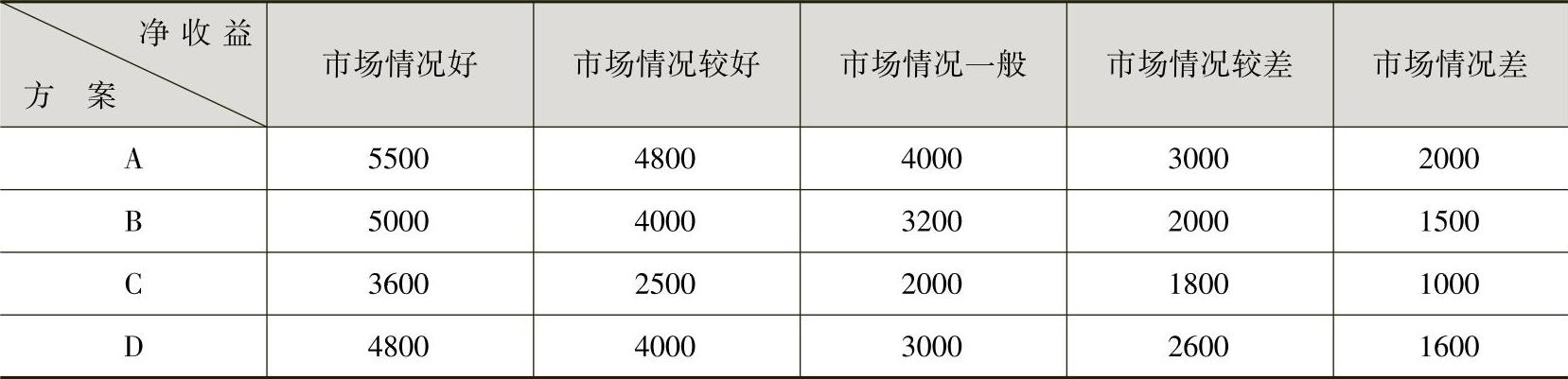
[例15-5]某房地产公司针对某一投资项目拟定了A、B、C、D四种投资方案。这四种方案的净收益情况与房地产市场的需求情况密切相关。据分析，未来五种市场状态的净收益值如表15-8所示，而五种市场状态发生的概率无法确知，试分别用上述五种决策方法进行投资方案的决策。

表15-8 决策方案及其净收益值表 （单位：万元）

解：

（1）采用小中取大法进行投资方案决策。

根据小中取大法的思路，首先从每个方案中选择最小的净收益。分别是，方案A：2000万元；方案B：1500万元；方案C：1000万元；方案D：1600万元。其次，从上述四个最小的净收益中，选择最大的净收益，即2000万元，此净收益代表的方案A就是决策的最佳方案。

（2）采用大中取大法进行投资方案决策。(www.xing528.com)

根据大中取大法的思路，首先从每个方案中选择最大的净收益。分别是，方案A：5500万元；方案B：5000万元；方案C：3600万元；方案D：4800万元。其次，从上述四个最大的净收益中，选择最大的净收益，即5500万元，此净收益代表的方案A就是决策的最佳方案。

（3）采用乐观系数法进行投资方案决策。

根据乐观系数法的思路，首先确定乐观系数，这里假设α=0.3，则各方案的折中净收益数值为：

A方案：5500万元×0.3+2000万元×0.7=3050万元

B方案：5000万元×0.3+1500万元×0.7=2550万元

C方案：3600万元×0.3+1000万元×0.7=1780万元

D方案：4800万元×0.3+1600万元×0.7=2560万元

由此可见，当乐观系数α=0.3时，方案A为最优的方案。

（4）采用最小后悔法进行投资方案决策。

根据最小后悔法的思路，首先求各种自然状态下各方案的后悔值，如表15-9所示。

表15-9 各方案的后悔值 （单位：万元）

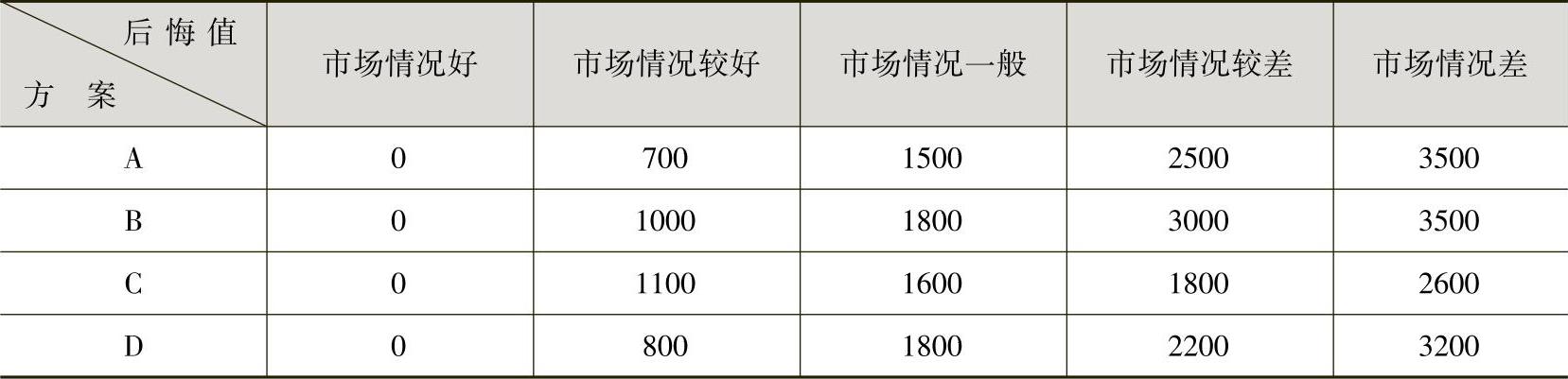
由表15-9可见，各方案的最大后悔值分别为：方案A：3500万元；方案B：3500万元；方案C：2600万元；方案D：3200万元。其次，从上述四个最大的后悔值中，选择最小的后悔值，即2600万元，此后悔值代表的方案C就是决策的最优方案。

（5）采用机会均等法进行投资方案决策。

根据机会均等法的思路，假设四个方案的机会均等，则各方案的利润期望值可以分别求得为：

E（A）=（5500+4800+4000+3000+2000）万元×1/5=3860万元

E（B）=（5000+4000+3200+2000+1500）万元×1/5=3140万元

E（C）=（3600+2500+2000+1800+1000）万元×1/5=2180万元

E（D）=（4800+4000+3000+2600+1600）万元×1/5=3200万元

由以上计算结果可知，方案A是决策的最优方案。