城市房地产投资项目的盈亏平衡分析动态化

上述介绍的都是静态盈亏平衡分析方法，它是企业在投资决策时常用的一种分析方法，它的优点是计算简便，成本不高，使用方便。因此，它在投资决策中被企业广为采用。即使在计算技术日益发达的今天，尤其是在进行小型投资决策时，企业依旧以静态盈亏平衡分析方法作为项目风险分析的评估工具。

但是，静态盈亏平衡分析方法也存在着明显的缺点，主要表现为：①它没有考虑投资项目周期现金流量，因此，其计算结果和结论是粗略的。通过盈亏平衡分析仅仅可以考察项目在正常生产年份的产量、销售价格等发生变化时，对于项目盈亏会产生多大的影响。但是项目整个周期的现金流量变化，对于项目盈亏会产生多大的影响，从静态盈亏平衡分析中看不出来。因此，运用此方法进行投资分析有可能产生错误结果。②它并未考虑资金时间价值这一因素对现金流量的影响，从而也就难以正确评价项目投资抵御风险的能力，由此也有可能导致一些错误的决策。因此，企业投资决策中应将其作为辅助方法来加以运用。

动态盈亏平衡分析，就是考虑资金时间价值，通过考察城市房地产投资项目整个周期内的产量、现金流入、现金流出三者的关系，测算项目的盈亏平衡点，来进行项目投资分析的一种方法。与静态盈亏平衡分析方法不同的是，此时的盈亏平衡点，是指项目在整个计算期内，项目的现金流入现值等于现金流出现值的那一点。在这一点上，项目刚好实现最低收益率，获得平均回报，即项目的净现值正好等于零。如果低于这一点所对应的生产水平，那么项目就会发生亏损；反之，则会获得超额利润。

动态盈亏平衡分析方法的运用也同样服从静态盈亏平衡分析方法的应用条件。为了推导动态盈亏平衡分析的公式，这里进一步作以下假设：项目投产后即达到正常设计生产能力；项目结束后固定资产残值为零且流动资金不再回收。根据上述假设条件可知：

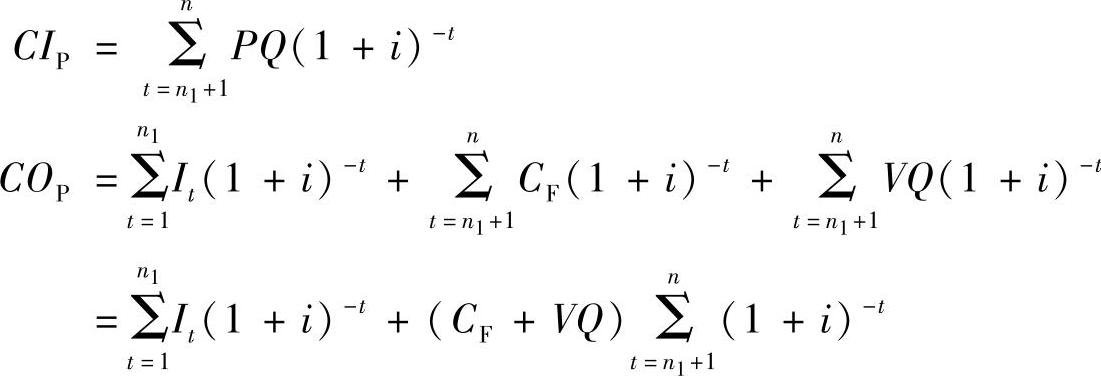
式中，CI_P为项目现金流入现值；CO_P为项目现金流出现值；I_t为项目第t年的建设投资；C_F为项目经营成本中不包括可变成本的固定成本总额；V为单位产品变动成本；n为项目周期；n₁为项目投资建设期；i为项目的贴现率；其他符号含义同静态盈亏平衡分析。

根据盈亏平衡的定义，在项目盈亏平衡时，项目现金流入现值等于项目现金流出现值，则有：

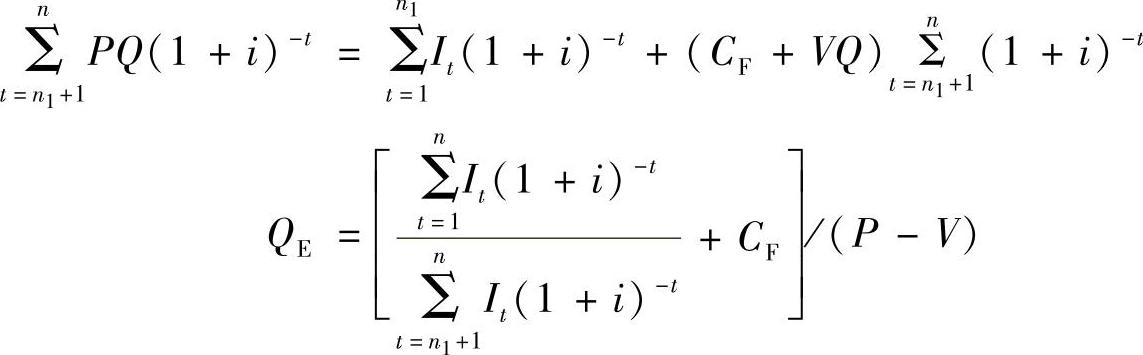
式中，Q_E为以产量表示的盈亏平衡点。

为了便于直观地分析项目盈亏平衡情况，同样可以把现金流入、现金流出与产量的关系，用盈亏平衡图的方式表示出来，如图13-3所示。

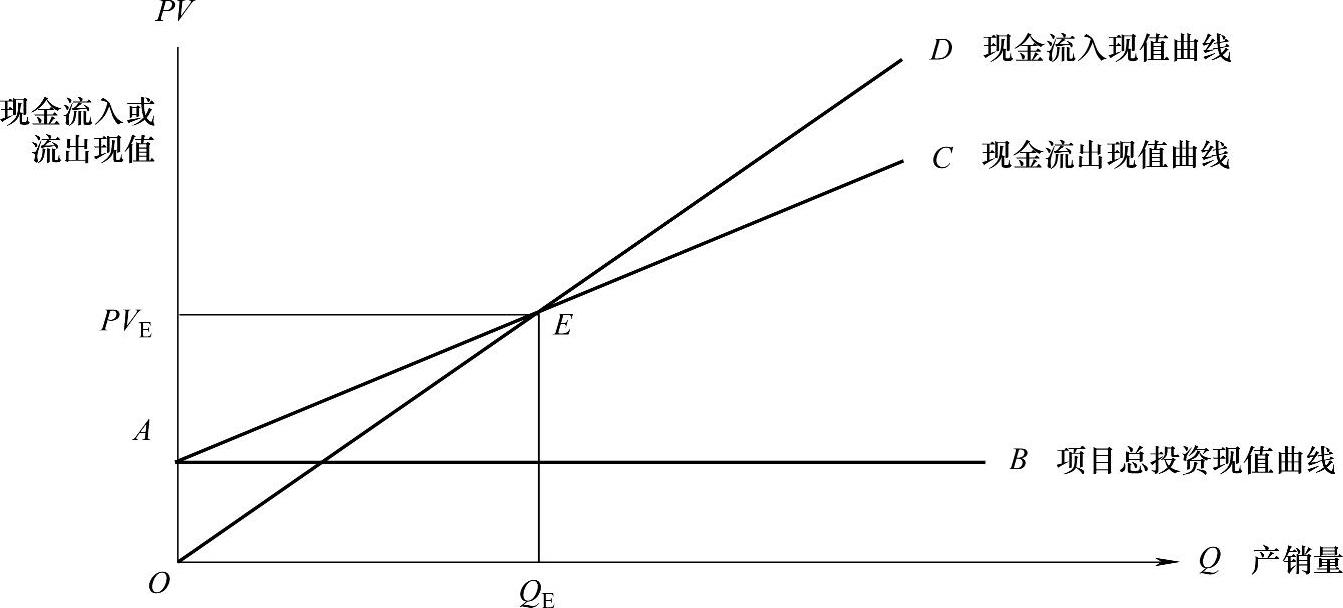
图13-3 动态线性盈亏平衡分析图

由图13-3可以看到，OD是现金流入现值曲线，AC是现金流出现值曲线，AB是项目总投资现值曲线。OD与AC的交点就是项目现金流入现值等于现金流出现值的盈亏平衡点。Q_E表示与盈亏平衡点相对应的项目产销量，PV_E表示与盈亏平衡点相对应的项目现金流入现值或现金流出现值。在AOE区域，现金流出现值高于现金流入现值，是亏损区；在CED区域，现金流入现值高于现金流出现值，是超额盈利区。

同静态盈亏平衡分析一样，项目的动态盈亏平衡点的高低，也可用于分析和判断项目适应市场变化的能力和承受风险的能力。项目的盈亏平衡点低，则说明当项目投产后，即使其实际产销量和项目设计产销量存在较大偏差，项目仍能获得预期最低回报，因而，可以承受较大的风险。相反，如果这一盈亏平衡点太高，则说明其经受风险的能力较弱。根据动态盈亏平衡分析的原理，同样可以推导出考虑税金因素的影响，以及以产品销售价格、销售收入、生产能力利用率等其他形式表示的盈亏平衡点分析表示方式。

盈亏平衡分析虽然能够度量项目风险的大小，但并不能揭示产生项目风险的根源，例如，虽然我们知道降低盈亏平衡点就可以降低项目的风险，提高项目的安全性，也知道降低盈亏平衡点可采取降低固定成本的方法，但是如何降低固定成本，应该采取哪些可行的方法或通过哪些有利的途径来达到这个目的，盈亏平衡分析并没有给我们答案，还需采用其他方法来帮助达到这个目标，因此在应用盈亏平衡分析时应注意使用的场合及欲达到的目的，以便能够正确运用这种方法。

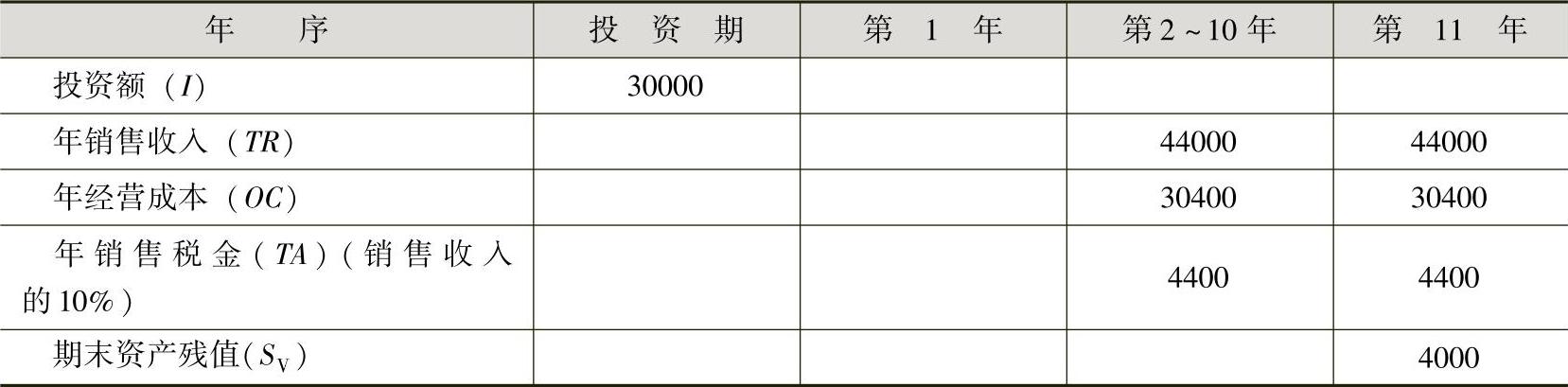
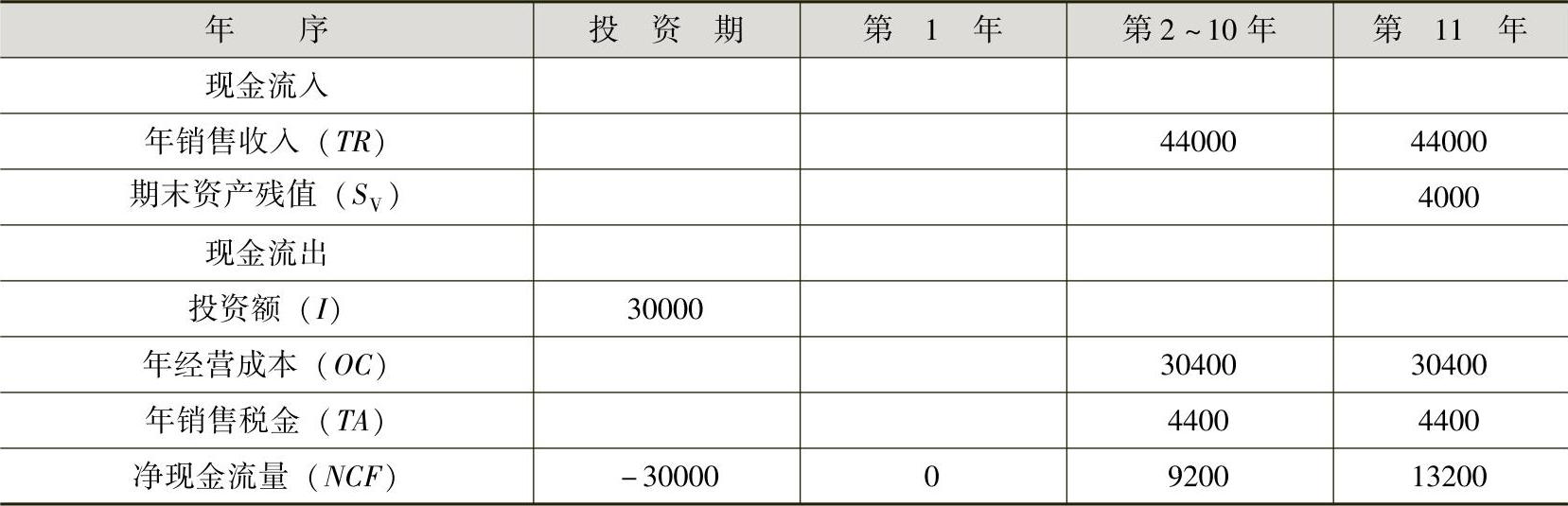
[例13-3]有一个城市房地产投资开发项目，其投资额、年销售收入、年经营成本、年销售税金、期末资产残值如表13-2所示。由于对未来影响经济效益的某些因素把握不大，其投资额、经营成本和产品价格均有可能在±20%的范围内变动，设基准收益率为10%，试进行动态盈亏平衡分析。

表13-2 城市房地产投资开发项目数据表 （单位：万元）

解：

根据上表数据，可以编制该项目的现金流量表，如表13-3所示。

表13-3 房地产投资开发项目现金流量表 （单位：万元）

(www.xing528.com)

根据净现值计算公式，可求出本项目的净现值为：

NPV为22793万元是在确定情况下的数值。题中，投资额、经营成本和产品价格均有可能在±20%的范围内变动，因此，需要考虑投资额与经营成本的变动。

为计算的方便，假设投资额变动的百分比为x，经营成本变动的百分比为y，则两个因素同时变动对方案净现值影响的计算公式为：

NPV=-I（1+x）+[TR-OC（1+y）-TA]（P/A，10%，10）（P/F，10%，1）+S_V（P/F，10%，11）

将表中的数据代入上式，经整理可得：

NPV=22793-30000x-169800y

取NPV的临界值，即令NPV=0，则有：

y=-0.1767x+0.1342

分别取x为10%、20%、30%、40%、50%、60%、70%，可以得到相应的y值分别为11.7%、9.9%、8.1%、6.49%、4.6%、2.8%、1.1%，根据这些值可以作出y=-0.1767x+0.1342的图像，该图像是一条直线，它是NPV=0的临界线，它与x轴交于（75.94%，0），与y轴交于（0，13.42%）。

当NPV＞0，则y＜-0.1767x+0.1342，即在临界线左下方的区域为盈利区，右上方为亏损区，如图13-4所示。也就是说，无论投资额与经营成本如何变动，只要其变动率的组合落在临界线的左下方，开发项目就可以实现盈利。

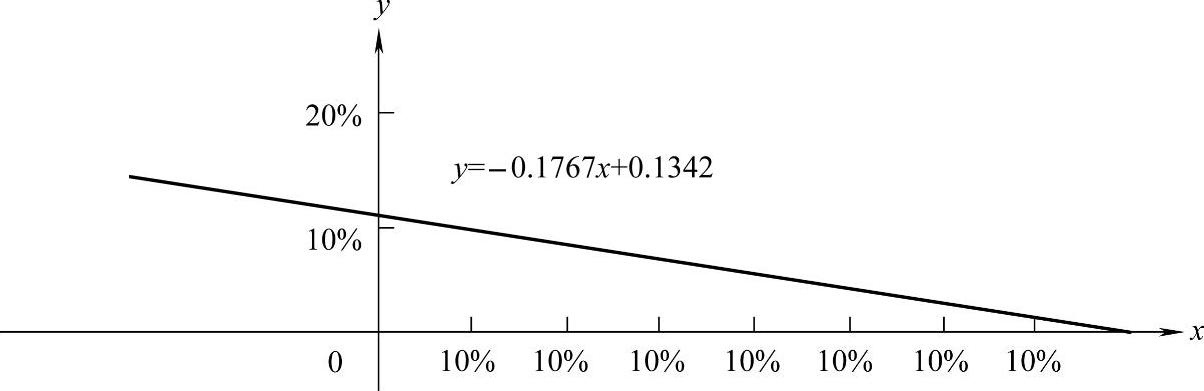
图13-4 动态盈亏平衡分析图一

在二维动态盈亏平衡分析的基础上，还可以进行三维动态盈亏平衡分析。当投资额、经营成本、产品价格同时变动时，设产品价格变动的百分比为z，产品价格的变动将导致销售收入和销售税金的变动，销售收入和销售税金变动的比例与产品价格变动的比例相同，对净现值的影响可以表示为：

NPV=-I（1+x）+[（TR-TA）（1+z）-OC（1+y）]（P/A，10%，10）（P/F，10%，1）+S_V（P/F，10%，11）

代入有关数据，经整理可得：

NPV=22793-30000x-169800y+221186z

令NPV=0，则有：22793-30000x-169800y+221186z=0

这是一个三维空间上的盈亏分界面，斜面的上方为盈利空间，它与x轴交于（75.94%，0，0），与y轴交于（0，13.42%，0），与z轴交于（0，0，-10.3%）（见图13-5）。也就是说，无论投资额、经营成本和产品价格如何变动，只要其变动率的组合落在临界面的上方，方案就可以盈利。

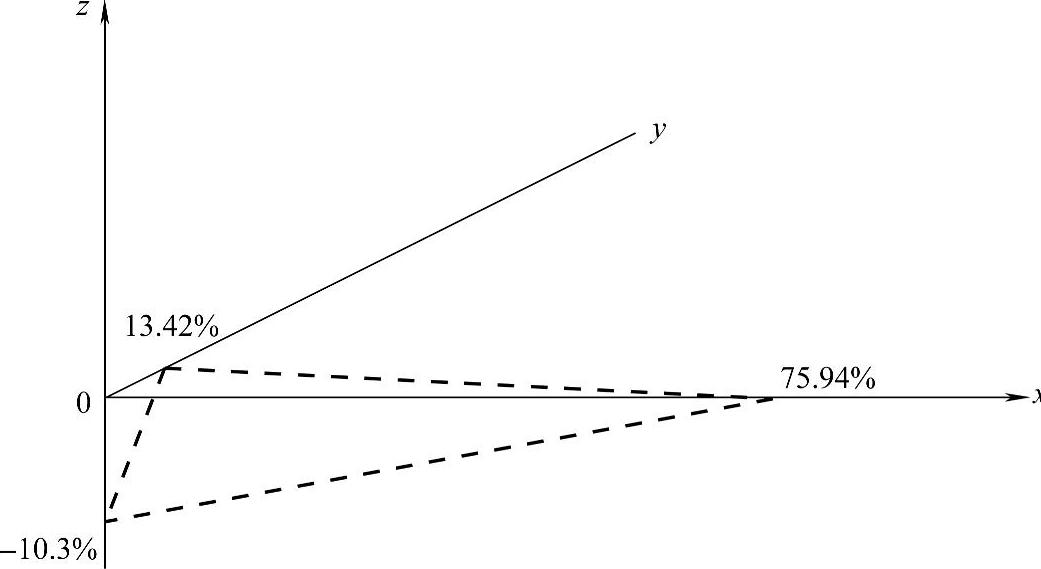
图13-5 动态盈亏平衡分析图二