非线性盈亏平衡分析的原理与方法

线性盈亏平衡分析是在假设销售收入和生产总成本与产销量呈线性关系的条件下进行的，但这只是一种理想的状态。在客观经济实际中，固定成本、单位产品变动成本和售价等均会发生变动，销售收入和生产成本与产销量的关系不是线性关系。为了更为准确地分析相关指标的盈亏平衡问题，就需要采用非线性盈亏平衡分析方法。

下面通过图13-2对非线性盈亏平衡分析方法进行简要说明。

以纵轴表示收入或成本，横轴表示开发（租售）数量Q，图中平行于横轴的直线表示固定成本线C_F，两条曲线表示总成本线TC和租售收入线TR。TC线与TR线的两个交点A₁和A₂均为盈亏平衡点，A₁和A₂分别对应开发数量Q₁^∗和Q₂^∗，即为盈亏平衡时的开发（租售）数量。从图中可以看出：

当Q₁^∗＜Q＜Q₂^∗时，项目盈利。

当0≤Q＜Q₁^∗或Q＞Q₂^∗时，项目亏损。

当Q=Q₁^∗或Q=Q₂^∗时，项目不盈不亏。

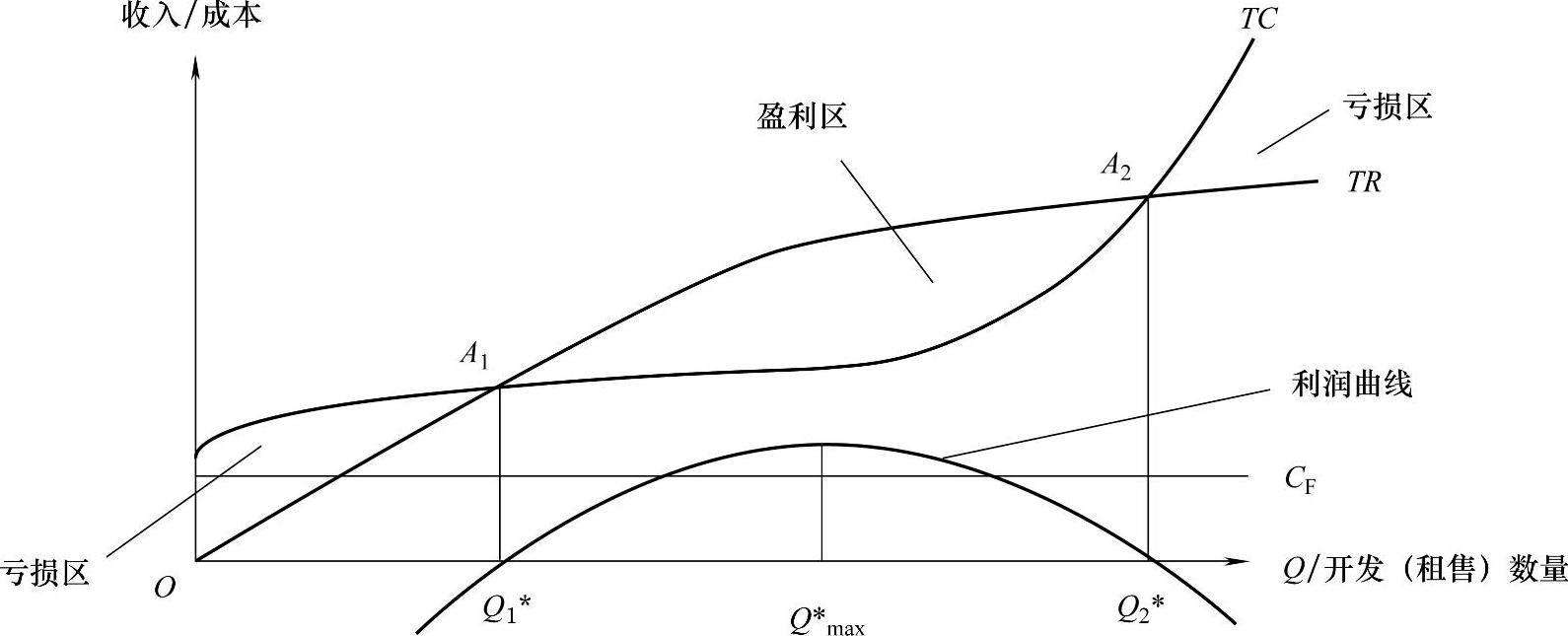
图13-2 非线性盈亏平衡分析图

利润最大时的产量（租售量）为Q^∗_max。

让收入曲线和成本曲线的函数式相等，可以从中解出Q₁^∗和Q₂^∗。求出Q₁^∗和Q₂^∗后就可以知道盈利区的具体范围，在该范围内，可以求出企业最大利润时的开发量或租售量。

E（Q）=TR（Q）-TC（Q）

令：

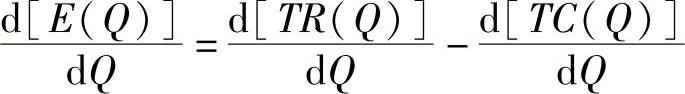
则：

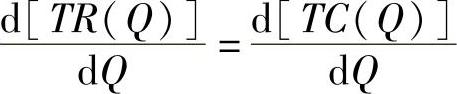
由此可求得利润极值时的产量。(www.xing528.com)

由于有时盈利区和亏损区从图中难以看出，求出的开发量或租售量是否对应着最大利润值还无法判别，因此还需要通过二次求导，利用极值原理加以判定。即

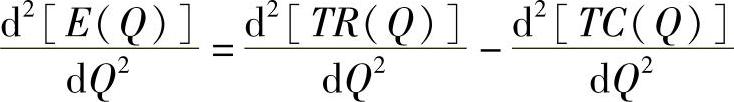
如果上式小于零，则求得的产量就是利润最大时的开发量或租售量；反之，则为亏损最大时的开发量或租售量。

[例13-2] 某开发公司计划开发一幢住宅，经过市场调研及历年来的资料分析，预计该住宅年销售收入函数及成本函数分别为：

TR=3100Q-0.6Q²

TC=3187500+600Q-0.2Q²

试确定该住宅的盈亏平衡点及最大盈利点。

解：这是一个非线性盈亏平衡分析的问题。根据盈亏平衡点的定义，可知在盈亏平衡点处有TR=TC，即

3100Q-0.6Q²=3187500+600Q-0.2Q²

整理得到：0.4Q²-2500Q+3187500=0

解上述方程可得：Q₁^∗=1500m²，Q₂^∗=8500m²，即产品的盈利区在产量介于1500m²到8500m²之间。

根据最大盈利点的含义，当产量水平达到最大盈利点时，应有：

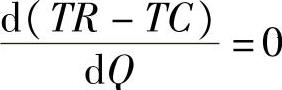
即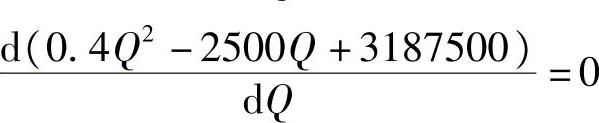

解得Q^∗_max=3125m²，即当产量水平达到3125m²时，该产品将获得最大的利润。