线性盈亏平衡分析的条件及方法

线性盈亏平衡分析是指收入、成本、利润等均和产量呈线性关系的盈亏平衡分析。它一般需要满足以下五个条件：

（1）在所分析的租售范围内，产品的固定成本与单位租售价格在产品租售期间保持不变。

（2）产品的变动成本是建筑面积（或产销量）的正线性函数。

（3）产品的开发量和销售量相等，即开发的房地产全部租售出去。

（4）产品的总销售收入和生产总成本是房地产开发面积（或产品产量）的线性函数。

（5）计算所使用的各种数据是正常生产年度的数据。

线性盈亏平衡分析一般有解析法和图解法两种方法。

1.线性盈亏平衡分析的解析法

解析法是指通过数学解析方法计算出盈亏平衡点的一种方法。

设某开发项目的总成本为TC，其中固定成本为C_F，变动成本为C_V，单位变动成本为V，开发数量为Q，总收入（销售收入）为TR，销售税率为r，销售单价为P，利润为E，则根据盈亏平衡的概念，当项目达到盈亏平衡状态时，其收入与支出恰好相等。即TR=TC。根据前面所做的假设，可得：

TR=PQ（1-r）

TC=C_F+C_V=C_F+VQ

E=TR-TC=PQ（1-r）-（C_F+VQ）

当TR=TC时，E=0，即利润等于零，项目投资不盈不亏。

上述线性盈亏平衡分析模型E=TR-TC=PQ（1-r）-（C_F+VQ）中，含有6个相互联系的变量，只要给定其中的5个，便可以求出另外一个变量的值。例如：

（1）求预期利润时：

E=PQ（1-r）-（C_F+VQ）

（2）求销售量时：

当E=0，即开发项目达到盈亏平衡时，项目的销售量（生产单一房地产产品时）Q^∗为：

当开发项目的产（销）量达到Q^∗时，投资项目的总收入与总支出相等。也就是说，Q^∗是房地产开发项目在预定的售价下，为了实现盈亏平衡所必须达到的最低销售量。

Q^∗与预计产品销售量之间的差距越大（小），说明该房地产开发项目承受市场风险的能力越强（弱）。

分析盈亏平衡销售量还需计算销售量允许降低的最大幅度（η_Q）。其计算公式为：

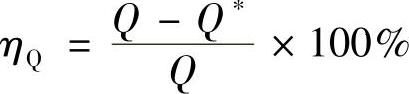
通过市场调查与预测，可以判断最大幅度（η_Q）出现的可能性。可能性越大，说明项目的风险越大，反之则风险越小。

（3）求销售单价时：

盈亏平衡（E=0）时，销售单价P^∗为：

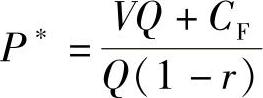
P^∗表示开发项目产品售价下降到预定可接受的最低盈利水平（一般为不亏不盈）时的最低售价。

P^∗与预计售价之间的差距越大（小），说明该房地产开发项目承受风险的能力越强（弱）。

分析盈亏平衡销售单价还需计算销售单价允许降低的最大幅度（η_P）。其计算公式为：

通过市场调查与预测，可以判断最大幅度（η_P）出现的可能性。可能性越大，说明项目的风险越大，反之则风险越小。

（4）求销售收入时：

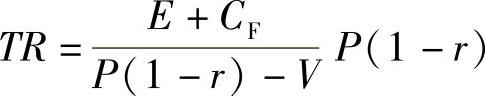
盈亏平衡（E=0）时，最低销售收入TR^∗为：

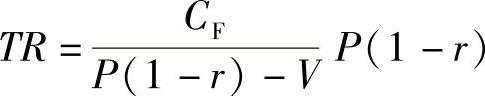
TR^∗为开发项目不发生亏损的最低销售收入。TR^∗与预计销售收入差距越大（小），说明该房地产开发项目的抗风险能力越强（弱）。

分析盈亏平衡销售收入还需计算销售收入允许降低的最大幅度（η_TR）。其计算公式为：

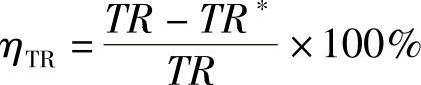
通过市场调查与预测，可以判断最大幅度（η_TR）出现的可能性。可能性越大，说明项目的风险越大；反之，则风险越小。

（5）求单位变动成本时：(www.xing528.com)

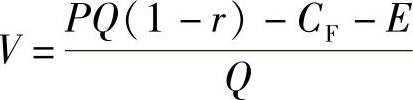
（6）求固定成本时：

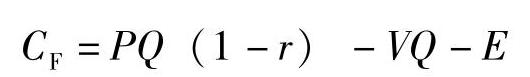
以上主要针对销售为主的开发项目在盈亏平衡状态时的销售量、销售单价与销售收入。当房地产产品以出租为主时，可相应进行盈亏平衡租金、盈亏平衡出租面积及盈亏平衡出租率等的计算分析。

[例13-1]已知某房地产开发项目固定成本为1000万元，单位变动成本为1000元/m²，销售税率为6%，其他数据及要求工作如表13-1所示。

表13-1 数据及要求工作

解：

已知：C_F=1000万元，V=1000元/m²

假设一：已知：P=2500元/m²，E=500万元

将已知条件代入计算式，便得：

Q^∗=1000元×10⁴/[2500×（1-6%）-1000]元/m²=7407m²

Q_X=（500×10⁴+1000×10⁴）元/[2500×（1-6%）-1000]元/m²=11111m2

计算表明，该项目最少要开发7407m²的商品房，才能保证不会亏损。若希望盈利500万元，则应至少开发11111m²的商品房。

假设二：已知：Q=50000m²，E=1000万元

将已知条件代入计算式，便得：

P^∗=（1000×10⁴+1000×5×10⁴）元/[5m²×10⁴×（1-6%）]=1277元/m²

P_X=（1000×10⁴+1000×10⁴+1000×5×10⁴）元/[5m²×10⁴×（1-6%）]

=1489元/m²

计算表明，该项目定价最少为1277元/m²，才能保证不会亏损。若希望盈利1000万元，则应把房价至少确定为1489元/m²。

假设三：已知：Q=50000m²，P=2000元/m²

将已知条件代入计算式，便得：

E=2000元/m²×50000m²×（1-6%）-1000元/m²×50000m²-1000元×10⁴

=3400万元

计算表明，当以市场平均销售价格销售时，本项目可以获得3400万元的利润，比预期利润（拟获利）多2400万元，说明本项目开发的可行性较高。

2.线性盈亏平衡分析的图解法

盈亏平衡分析既可以用前述的解析法分析，也可以利用图解法分析。图解法分析如图13-1所示。

图13-1 线性盈亏平衡分析图

图13-1中，以纵轴表示总成本TC或总收入TR，横轴表示开发（租售）数量Q，图中的四条直线分别表示固定成本线C_F、变动成本线C_V、总成本线TC和租售收入线TR。总成本线和租售收入线的交点即为盈亏平衡点，A点所对应的开发（租售）数量Q^∗，即为盈亏平衡时的开发数量（或租售量），或称保本量，其数额大小可在坐标轴上查得。AQ^∗线将图示区域分隔为两个部分，左侧总成本线高于租售收入线，为亏损区，右侧总成本线低于租售收入线，为盈利区。或者说，当Q＞Q^∗时，项目盈利；当0≤Q＜Q^∗，项目亏损；当Q=Q^∗时，项目不盈不亏。

由此可见，盈亏平衡点越低，达到该点的开发量（或租售量）、销售收入及成本也就越少，只要开发少量的房地产产品就能达到项目的收支平衡。所以，盈亏平衡点的值越小，项目的盈利机会就越大，亏损的风险就越小。

绘制盈亏平衡分析图，可根据解析法的有关计算公式和具体数据，按下列步骤进行：

（1）选定直角坐标系，以成本或收入为纵轴，以开发量或租售量为横轴。

（2）在纵轴上找出固定成本数值，以此为起点，绘制一条与横轴平行的固定成本线。

（3）以固定成本线的起始点为起点，以单位变动成本为斜率，绘制总成本线。

（4）以坐标原点为起点，以单价为斜率，绘制销售收入线。

这样就得到一个具体的盈亏平衡分析图，相关数据可以直接从该图中得到。

盈亏平衡分析图表达的意义如下：

（1）固定成本线与横轴之间的垂直距离为固定成本值，它不因开发量（或租售量）的增减而变动。

（2）总成本线与固定成本线之间的垂直距离为变动成本，它随开发量（或租售量）的增减而呈正比例的变动。

（3）总成本线与横轴之间的垂直距离为总成本，它是固定成本与变动成本之和。

线性盈亏平衡分析方法简单明了，有助于我们尽快地全面把握决策的目的，但这种方法在应用中有一定的局限性，主要表现在对投资项目来讲，在实际的生产经营过程中，收益和支出与产品产量之间的关系往往呈现出一种非线性的关系，而非我们所假设的线性关系。这时就需要用到非线性盈亏平衡分析方法。