动态盈利指标及计算方法

动态盈利指标采用了折现现金流量的方法，其计算特点是考虑了资金时间价值，能如实反映资金实际运用情况和全面体现项目整个寿命期内的经济活动和经济效益，因而比静态盈利指标更能够准确地对项目财务效益作出符合实际的评估。其主要分析指标有：

1.净现值（NPV）

（1）含义与计算公式。净现值是反映项目在整个寿命期内总的获利能力的主要动态评价指标。它是指按照投资者最低可接受的收益率或设定的基准收益率i_c，将房地产项目开发经营期内各期净现金流量折现到开发期期初的现值之和。

以i_c为例，其表达式为：

式中，CI为现金流入量；CO为现金流出量；（CI-CO）_t为第t期期末的净现金流量，t=0表示开发期期初或第0期期末；n为计算期（n=1，2，3，…，n）；i_c为财务基准收益率或设定的收益率。

净现值指标表示用现金流入现值补偿现金流出现值后的余额，可通过全部投资现金流量表和自有资金现金流量表中的净现金流量求得。

（2）净现值的作用。净现值是用来判别投资项目是否可行的动态评价指标，它可能大于等于零，也可能小于零。净现值评价标准的临界值是零。

当NPV＞0，则表明投资项目的收益率大于基准收益率或贴现率所预定的投资收益水平，该项目是可以考虑接受的。

当NPV=0，则表明投资项目的收益率正好等于基准收益率或贴现率所预定的投资收益水平。此时该项目是否可以被接受，要看基准收益率或贴现率是否大于银行长期贷款利率，如果是，则项目是可以考虑接受的，否则此项目一般不可行。

当NPV＜0，则表明投资项目的收益率小于基准收益率或贴现率所预定的投资收益水平，该项目一般是不可以接受的。

（3）净现值指标的优缺点。净现值指标是投资分析与评价中最常用的一个指标，在房地产投资分析中也得到了广泛的应用。它的优点是考虑了项目寿命期内各年现金流量的现值，在投资总额相等的情况下可以按净现值的大小对项目或备选方案排序。

但是净现值指标的缺点也是明显的，主要表现在以下几点：

1）如果投资总额不等，仅仅根据净现值的大小进行决策就可能导致失误，同时，净现值不能反映项目或备选方案的确切的收益水平。

2）贴现率不易确定。贴现率是计算净现值必不可少的数据，它的准确与否，对净现值的影响很大，尤其对长期经营项目和后期资金流量较大的项目更为明显。

因此，净现值指标计算虽然较简单，能够反映项目在整个计算期内的绝对效果，但不能反映单位投资的效果。为了克服净现值在投资总额不等的情况下不能排序的缺点，有时也有必要计算净现值率以及内部收益率指标。

2.净现值率（NPVR）

净现值率是项目净现值与全部投资现值的比值，即单位投资的净现值，是反映项目效果的相对指标。其表达式为：

NPVR=NPV/I

式中，NPV为净现值；I为总投资额的现值。

净现值率可以作为净现值的一个补充指标。一般来说，不同的方案中，净现值率大的方案为可选方案。

与净现值相对应，净现值率也有三种情况，即净现值率大于零、等于零或小于零。

[例12-4] 设某房地产项目有三个开发投资方案（见表12-7），试选择最佳投资方案。

表12-7 三个开发投资方案

解：

分别计算各方案的净现值率：

方案一：NPVR=1500万元/8200万元×100%=18.29%

方案二：NPVR=1050万元/5100万元×100%=20.59%

方案三：NPVR=800万元/3000万元×100%=26.67%

计算结果说明，虽然方案一、二的净现值大于方案三，但方案三的净现值率大于方案一、二，因此方案三才为最佳方案。

该例说明，净现值大的方案不一定净现值率也大，选取投资方案应综合分析各种因素和指标。

3.内部收益率（IRR）

（1）内部收益率的本质含义。根据净现值的计算公式，如果现金流量每年不变，则净现值将随折现率的变化而成反方向变化，即净现值与折现率呈反向变动关系，如图12-2所示。

图12-2中，当i值小于IRR时（如i₁），对于所有的i值，NPV都是正值；当i值大于IRR时（如i₂），对于所有的i值，NPV都是负值；在折现率由小到大取值的过程中，必有一个折现率使得净现值等于零，这个折现率就是内部收益率IRR。

由此可见，房地产项目的内部收益率是指房地产项目在整个开发经营期内各期净现金流量现值累计等于零时的折现率。内部收益率又称内部报酬率或预期收益率，反映了拟投资项目的实际投资收益水平，是考察项目盈利能力的主要动态指标。

图12- 净现值与折现率的关系图

实际财务分析中，具体的投资项目可以计算两种IRR指标，即全部投资内部收益率和资本金（自有资金、权益投资）内部收益率。

内部收益率的表达式为：

式中，IRR为内部收益率，其他字母含义同净现值公式中的字母含义。

从经济角度来看，内部收益率是指在这样的折现率下，到项目计算期终了时，当初的所有投资都可以完全被收回。

（2）内部收益率的具体计算。由内部收益率的上述公式可以看出，正向求解IRR需要求解一个高次方程，难度很大。一般需要借助计算机软件或功能很强的计算器完成。如果用手工计算，应先采用试算法，后采用内插法来求解出IRR的近似值。

内插法的公式为：

式中，i₁为当净现值为接近于零的正值时的折现率；i₂为当净现值为接近于零的负值时的折现率；NPV₁为采用低折现率时的正净现值；NPV₂为采用高折现率时的负净现值。

式中i₁与i₂之差不应超过2%。否则，折现率i₁、i₂和净现值之间不一定呈线性关系，从而使所求得的内部收益率失真。

内部收益率的公式也可以用文字表示如下：

试算法的具体步骤为：

1）用估计的某折现率对拟投资项目整个计算期内各年的净现金流量进行折现，并得出净现值。如果得到的净现值等于零，则所选定的折现率即为内部收益率。如果所得到的净现值为一正数，则再选一个更高一些的折现率，再次试算，直到正数净现值接近于零为止。该步骤得到的净现值和折现率分别为NPV₁和i₁。

2）在第一步的基础上，继续提高折现率，直到计算出接近零的负数净现值为止。该步骤得到的净现值和折现率分别为NPV₂和i₂。

3）把前两步计算所得的正、负净现值及其相应的折现率，代入内插法计算公式求得内部收益率。

当财务报表按月、季或半年编制时，计算求出的内部收益率应换算为以年为期的单位的内部收益率，然后再与开发企业最低可接受的收益率进行比较。(www.xing528.com)

如以季为期的单位，则换算公式为：

IRR_年=[（1+IRR_季）4-1]×100%

（3）内部收益率的主要作用。内部收益率是项目折现率的临界值。在进行独立方案的分析评价时，一般是在求得投资项目的内部收益率后，与同期贷款利率i及同期行业基准收益率i_c相比较，以判定项目在财务上是否可行。其具体作用体现在：

1）可以指出投资者能够承受的贷款利率上限。内部收益率是项目贷款可以承受的贷款利率上限，超过这个界限，项目投资就会亏损。

2）与同期贷款利率i、基准收益率及投资者可接受的最低收益率（MARR）比较，以评判独立项目的取舍。

当IRR＞i，则项目盈利。

当IRR=i，则项目盈亏平衡。

当IRR＜i，则项目亏损。

当IRR＞i_c，则项目盈利超出行业平均收益水平。

当IRR=i_c，则项目盈利等于行业平均收益水平。

当IRR＜i_c，则项目盈利低于行业平均收益水平。

当IRR≥MARR，则项目盈利能力已满足投资者的最低回报要求。

当IRR＜MARR，则项目盈利能力不能满足投资者的最低回报要求。

上述几种情况中，IRR≥i_c≥MARR≥i时，项目在财务上是可以考虑接受的。投资开发商可以在此基础上，再根据其他方面的信息，决定是否进行项目的投资开发。

3）能够比较互斥项目单位投资回报的优劣。一般来说，内部收益率越大，盈利越多，盈利时间越早，因此，可以根据内部收益率的高低来分析项目的优劣。

由于内部收益率反映了项目的收益水平，而基准收益率是根据全国同行业平均先进收益水平确定的，所以要求项目的内部收益率必须大于或等于基准收益率；同时，应将项目的内部收益率和项目的资金成本率进行比较，在任何情况下，都应当要求内部收益率大于项目的资金成本率。

（4）内部收益率的优缺点。内部收益率指标与净现值比较，其优点是比较直观、容易理解，计算时不需要事先确定一个折现率；但其计算复杂、费事，需借助专用计算器或电子计算机才能达到比较满意的效果，而且也需要有一个基准内部收益率作为比较的标准。尤其需要注意的是，这个指标不能直接用于进行互斥方案的比较，在进行互斥方案比较时应用差额投资内部收益率指标。

（5）内部收益率存在的问题。有时，内部收益率作为评价指标得出的决策信号和其他指标，如净现值、净现值率等得出的结果相矛盾，其原因在于其自身存在以下问题：

1）再投资利润率问题。采用内部收益率法对各种项目进行比较时，暗含了这样一个假设，即回收期内的现金流入以内部收益率再投资。而这种假设成立的前提是，当时市场上其他各种可接受的投资机会的收益率与其内部收益率相同。这种假设在实际中很难成立，或者很难一直成立。所以用内部收益率作为再投资利润率显然是不合理的假设。这样，从理论上说，把内部收益率作为城市房地产投资项目的收益率是错误的，尤其对于几十年的房地产经营项目来说，该指标更是不能说明收益水平。但是，在现有城市房地产投资分析领域的复杂程度、投资者的收益水平和所有可能获得信息的条件下，人们仍然偏爱用相对简单的内部收益率法来判断一个投资项目的收益水平。

2）多重根问题。由于城市房地产投资开发模式不同，现金流量模式也不尽相同，投资项目会有许多不同的内部收益率。除了初始投资外，投资过程中有时仍会出现负现金流量，这种情况下，内部收益率的数量可能会与相反的现金流量（从正值到负值，或相反）数量一样多，即出现多重根现象。不过很多时候，尽管出现了相反的现金流量，内部收益率方程除了一个实数根外，其他都是虚根，即方程有且只有一个内部收益率解。

解决多重根的方法一般是，把投资过程中出现的负现值再折现到较大的正现值中，使净现值的符号只变化一次，这样就能得到一个净现值。

[例12-5]某投资者投资100万元购买一栋住宅用于出租，共租出10年。租约规定每年年初收租，前两年租金均为10万元，以后每两年租金增加10%，在租约期满后将住宅售出，得到收益90万元，假设投资项目的贴现率为12.5%。试计算投资项目的净现值，并求出本项目投资的内部收益率。

解：

根据题中已知数据，可以编制表12-8。

表12-8 投资额和租金收入或售价表 （单位：万元）

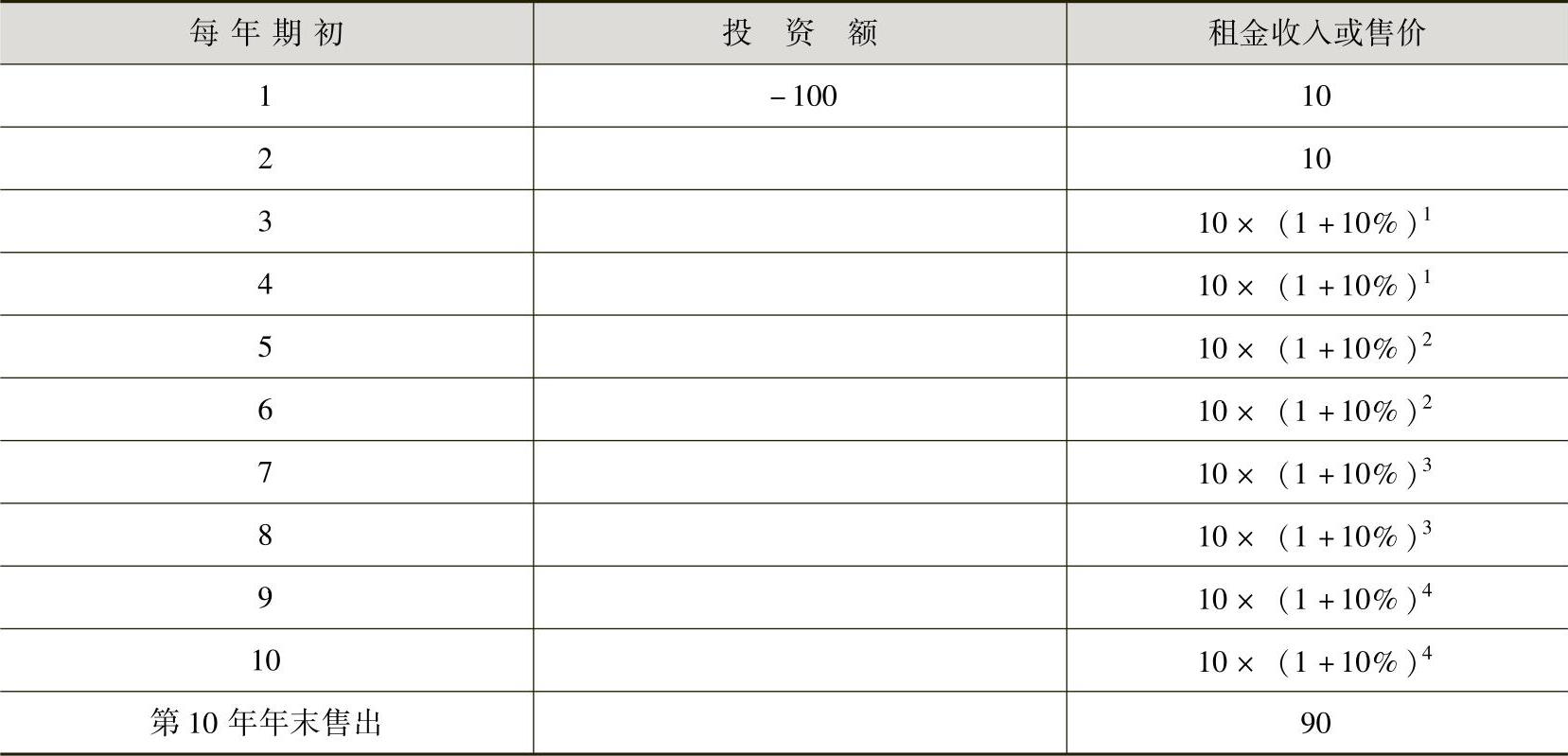
此净现值为一接近于零的正值。

假设贴现率为13%，再计算一次净现值。

净现值=售楼收入现值+租金总收入现值-投资额现值=-0.20万元

净现值为一接近于零的负值。采用内插法公式，可以求得：

以上计算表明投资者的投资回报率等于12.85%，高于12.5%的贴现率，项目可行。

4.动态投资回收期（P_t）

（1）含义与计算公式。动态投资回收期是指在基准折现率（或基准收益率）i_c条件下，项目从投资开始到项目收益偿付完投资额为止所经历的时间。其计算公式为：

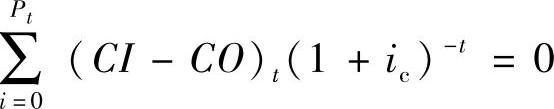
式中，P_t为动态投资回收期；其他字母含义同净现值公式中的字母含义。

动态投资回收期的计算公式也可以表示为：动态投资回收期=累计净现值出现正值期数-1+（上年累计净现值的绝对值/当年净现值）

动态投资回收期一般以年表示。其他时间单位可折算为年数，小数部分可折算为月数。

（2）主要作用。动态投资回收期指标一般用于评价开发完成后用于出租或经营的房地产项目需要多长时间收回开发经营投资成本。

计算得出的动态投资回收期要与行业基准动态投资回收期相比较，以判别项目的投资回收能力。当前者小于后者时，表明该项目的投资能在规定的时间内收回。

动态投资回收期这一指标特别适用于风险较大的投资项目。一般来说，预先有确定的标准动态投资回收期，用计算出来的动态投资回收期和标准动态投资回收期进行比较，如果某方案的动态投资回收期小于标准动态投资回收期，则该方案可以考虑接受，反之则不可取。

（3）主要优缺点。与静态投资回收期指标相比较，动态投资回收期的优点是考虑了资金的时间因素，能够真正反映资金的回收时间，其缺点是计算比较复杂。通常，在静态投资回收期不长或折现率不大的情况下，不影响项目评价或方案的比较选择。但在静态投资回收期较长的情况下，两种投资回收期的差别可能比较明显。

动态投资回收期也有明显的局限性。这一指标只强调投入资本的回收快慢，而忽视了投入资本的盈利能力，更没有考虑投资回收以后的收益情况。因此，一般来说，不应以动态投资回收期来作为评价投资方案的主要指标，只能作为辅助指标。

[例12-6] 续例12-5。试求项目的动态投资回收期。

解：

根据例12-5给定的表格，编制表12-9。

表12-9 累计折现值表 （单位：万元）

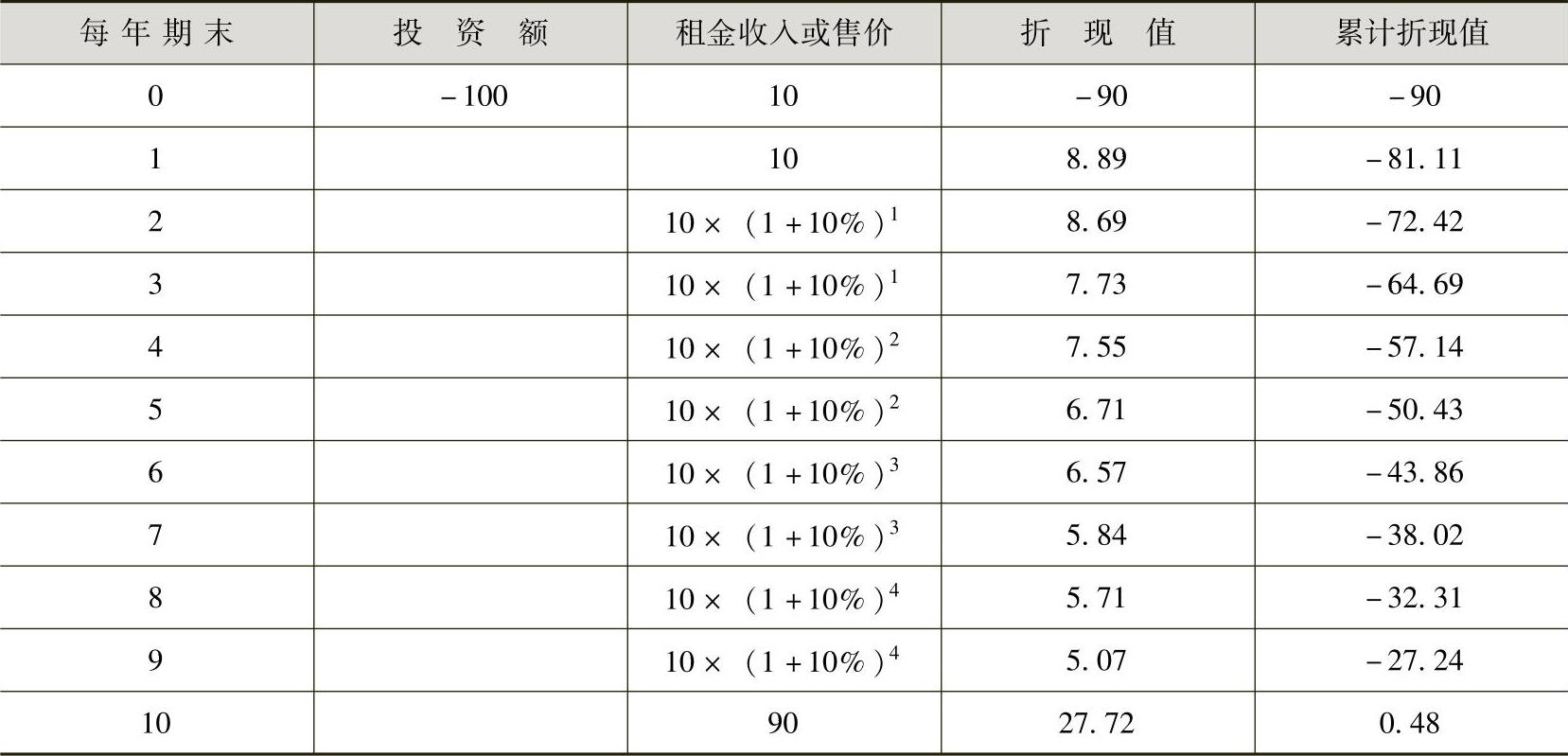
由此可见，出现正值的年份为第10年，根据计算公式：

动态投资回收期=累计净现值出现正值期数-1+（上年累计净现值的绝对值/当年净现值）

代入数据：

动态投资回收期=10年-1+27.24万元/27.72万元=9.98年

实际上，在9.98年的时候，本项目投资的住宅并没有售出，因此，项目投资并没有收回。真正收回投资的时间应该在第10年年末，即住宅卖出的时刻，即动态投资回收期应该为10年。这说明了动态投资回收期和实际的回收期并不一致，也表明了利用数学公式得到的数据和实际往往并不相符。